So wenden sie den satz von tschebyscheff in excel an
Der Satz von Chebyshev besagt, dass für jede Zahl k größer als 1 mindestens 1 – 1/k 2 der Datenwerte in jeder trainierten Verteilung innerhalb von k Standardabweichungen vom Mittelwert liegen.
Beispielsweise liegen bei jeder geformten Verteilung mindestens 1 – 1/3 2 = 88,89 % der Werte in der Verteilung innerhalb von 3 Standardabweichungen vom Mittelwert.
Dieses Tutorial zeigt mehrere Beispiele für die Anwendung des Tschebyscheff-Theorems in Excel.
Beispiel 1: Verwenden Sie den Satz von Tschebyscheff, um zu bestimmen, wie viel Prozent der Werte für einen Datensatz mit einem Mittelwert von 50 und einer Standardabweichung von 10 zwischen 30 und 70 liegen.
Bestimmen Sie zunächst den Wert von k. Wir können dies tun, indem wir bestimmen, wie viele Standardabweichungen zwischen 30 und 70 vom Mittelwert liegen:
(30 – Mittelwert) / Standardabweichung = (30 – 50) / 10 = -20 / 10 = -2
(70 – Mittelwert) / Standardabweichung = (70 – 50) / 10 = 20 / 10 = 2
Die Werte 30 und 70 liegen jeweils 2 Standardabweichungen unter bzw. über dem Mittelwert. Also, k = 2 .
Anschließend können wir in Excel die folgende Formel verwenden, um den Mindestprozentsatz der Werte zu ermitteln, die innerhalb von 2 Standardabweichungen vom Mittelwert für diesen Datensatz liegen:
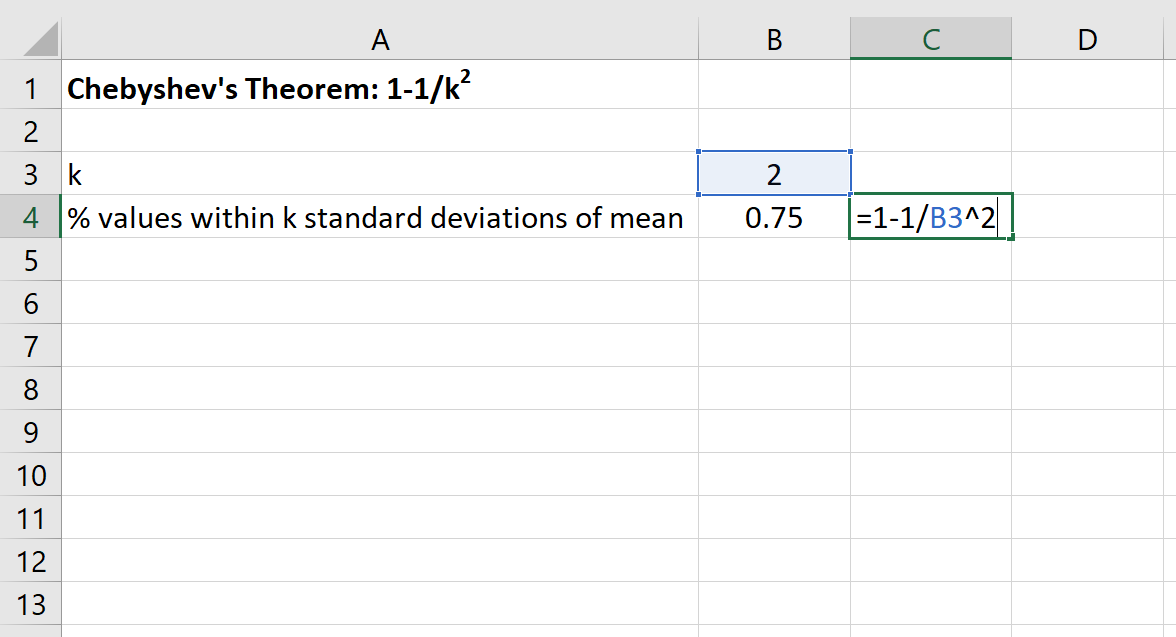
Der Prozentsatz der Werte zwischen 30 und 70 beträgt für diesen Datensatz mindestens 75 % .
Beispiel 2: Verwenden Sie den Satz von Tschebyscheff, um zu bestimmen, wie viel Prozent der Werte für einen Datensatz mit einem Mittelwert von 35 und einer Standardabweichung von 5 zwischen 20 und 50 liegen.
Bestimmen Sie zunächst den Wert von k. Wir können dies tun, indem wir bestimmen, wie viele Standardabweichungen zwischen 20 und 50 vom Mittelwert liegen:
(20 – Mittelwert) / Standardabweichung = (20 – 35) / 5 = -15 / 5 = -3
(50 – Mittelwert) / Standardabweichung = (50 – 35) / 5 = 15 / 5 = 3
Die Werte 20 und 50 liegen jeweils 3 Standardabweichungen unter bzw. über dem Mittelwert. Also, k = 3 .
Anschließend können wir in Excel die folgende Formel verwenden, um den Mindestprozentsatz der Werte zu ermitteln, die innerhalb von 3 Standardabweichungen vom Mittelwert für diesen Datensatz liegen:
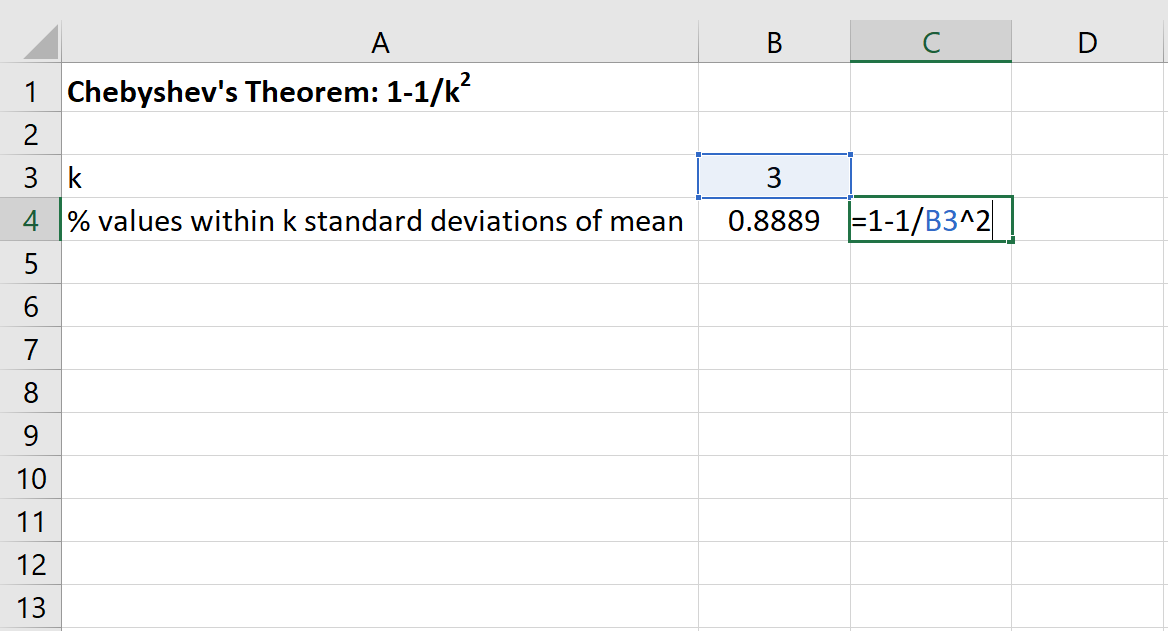
Der Prozentsatz der Werte zwischen 20 und 50 für diesen Datensatz beträgt mindestens 88,89 % .
Beispiel 3: Verwenden Sie den Satz von Tschebyscheff, um zu bestimmen, wie viel Prozent der Werte für einen Datensatz mit einem Mittelwert von 100 und einer Standardabweichung von 5 zwischen 80 und 120 liegen.
Bestimmen Sie zunächst den Wert von k. Wir können dies tun, indem wir bestimmen, wie viele Standardabweichungen zwischen 80 und 120 vom Mittelwert liegen:
(80 – Mittelwert) / Standardabweichung = (80 – 100) / 5 = -20 / 5 = -4
(120 – Mittelwert) / Standardabweichung = (120 – 100) / 5 = 20 / 5 = 4
Die Werte 80 und 120 liegen jeweils 4 Standardabweichungen unter bzw. über dem Mittelwert. Also, k = 4 .
Anschließend können wir in Excel die folgende Formel verwenden, um den Mindestprozentsatz der Werte zu ermitteln, die innerhalb von 4 Standardabweichungen vom Mittelwert für diesen Datensatz liegen:
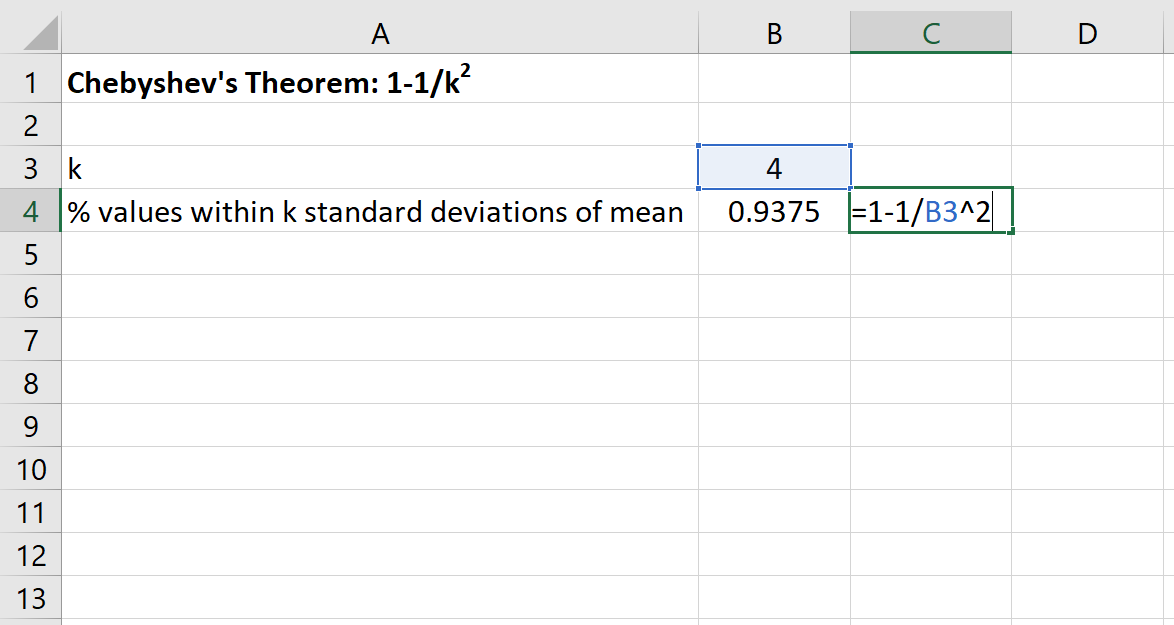
Der Prozentsatz der Werte zwischen 80 und 120 für diesen Datensatz beträgt mindestens 93,75 % .
Über den Autor
Dr. Benjamin Anderson
Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen