Schlussfolgerung und vorhersage: was ist der unterschied?

In Statistiken möchten wir Daten häufig aus einem von zwei Gründen verwenden:

(1) Schlussfolgerung: Wir möchten die Art der Beziehung zwischen den Prädiktorvariablen und der Antwortvariablen in einem vorhandenen Datensatz verstehen.

(2) Vorhersage: Wir möchten einen vorhandenen Datensatz verwenden, um ein Modell zu erstellen, das den Wert der Antwortvariablen einer neuen Beobachtung vorhersagt.

Angenommen, wir haben den folgenden Datensatz mit Informationen über Häuser:

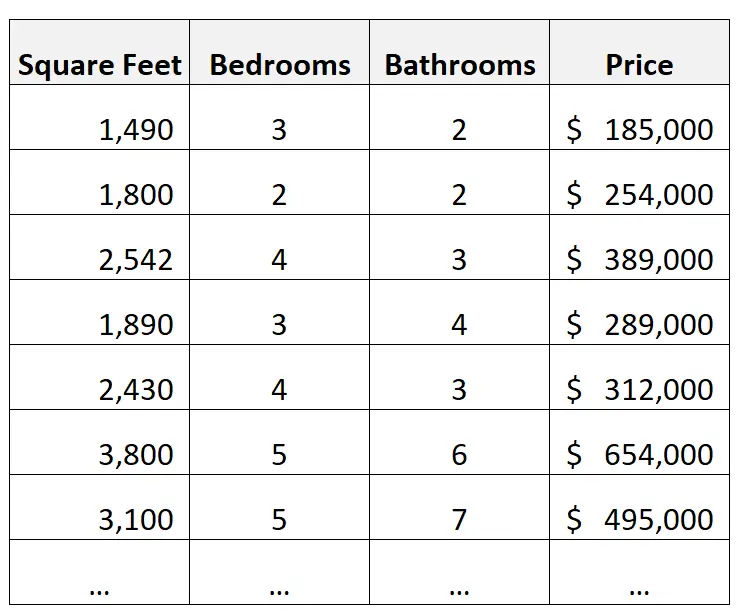
Ein Beispiel für eine Schlussfolgerung:

Angenommen, wir erstellen ein multiples lineares Regressionsmodell mit Quadratmeterzahl, Anzahl der Schlafzimmer und Anzahl der Badezimmer als Prädiktorvariablen und dem Preis als Antwortvariable.

Wir könnten dann die Regressionskoeffizienten verwenden, um die durchschnittliche Preisänderung zu verstehen, die mit einer Änderung um eine Einheit in jeder der Prädiktorvariablen verbunden ist.

Beispielsweise könnten wir nachvollziehen, wie stark sich der Preis (im Durchschnitt) mit jedem zusätzlichen Schlafzimmer, jedem zusätzlichen Badezimmer und jedem zusätzlichen Quadratmeter ändert.

Ein Beispiel für eine Vorhersage:

Wir könnten dasselbe multiple lineare Regressionsmodell erstellen und es verwenden, um den Wert eines neuen Hauses basierend auf seiner Quadratmeterzahl, der Anzahl der Schlafzimmer und der Anzahl der Badezimmer vorherzusagen.

Beispielsweise könnten wir das Modell verwenden, um den Preis eines neuen Hauses mit 3 Schlafzimmern, 3 Badezimmern und 2.000 Quadratmetern vorherzusagen.

Anschließend können wir unsere Prognose mit dem tatsächlichen Listenpreis vergleichen und beurteilen, ob das Haus unter- oder überbewertet erscheint.

Die folgenden Beispiele veranschaulichen den Unterschied zwischen Inferenz und Vorhersage in verschiedenen Szenarien:

Beispiel 1: Schlussfolgerung und Vorhersage im Sport

Angenommen, wir haben den folgenden Datensatz mit Informationen über professionelle Basketballmannschaften:

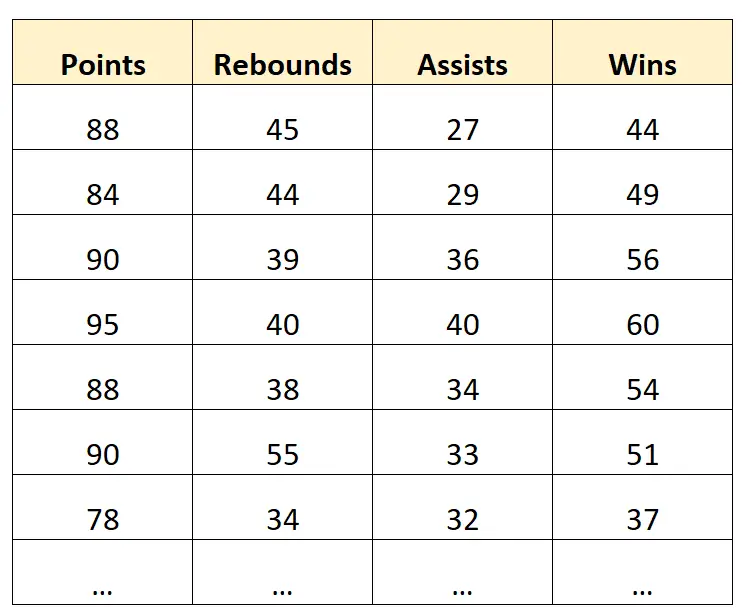
Ein Beispiel für eine Schlussfolgerung:

Angenommen, wir erstellen ein multiples lineares Regressionsmodell mit Punkten, Rebounds und Assists als Prädiktorvariablen und Gewinnen als Antwortvariable.

Mithilfe des Modells könnten wir dann verstehen, wie sehr sich die Anzahl der Siege (im Durchschnitt) mit jedem zusätzlichen Punkt, Rebound und Assist ändert.

Ein Beispiel für eine Vorhersage:

Wir könnten dasselbe multiple lineare Regressionsmodell erstellen und es verwenden, um vorherzusagen, wie viele Siege ein Team basierend auf der Anzahl seiner Punkte, Rebounds und Assists haben wird.

Beispielsweise könnten wir das Modell verwenden, um vorherzusagen, wie viele Siege ein Team mit 90 Punkten, 40 Rebounds und 30 Assists haben wird.

Beispiel 2: Schlussfolgerung und Vorhersage im Geschäftsleben

Angenommen, wir verfügen über den folgenden Datensatz mit Informationen zu den Jahresumsätzen (in Millionen) verschiedener Unternehmen:

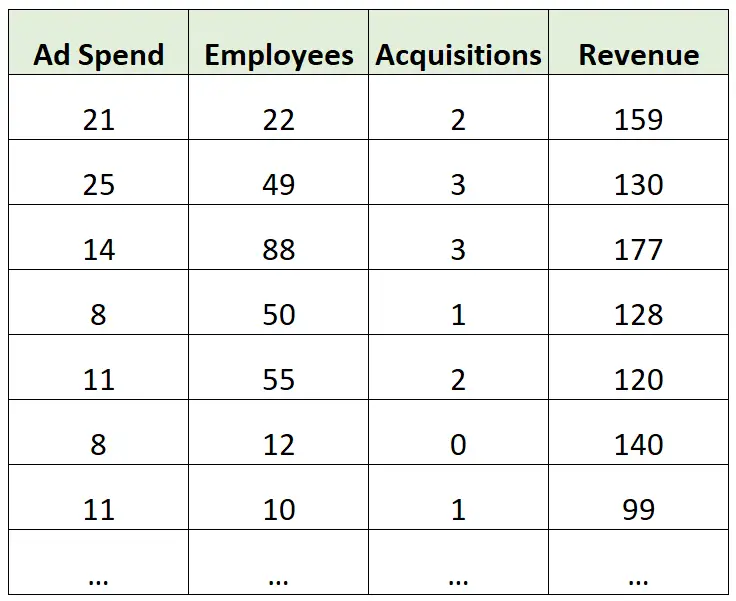
Ein Beispiel für eine Schlussfolgerung:

Angenommen, wir erstellen ein multiples lineares Regressionsmodell, das Werbeausgaben, Anzahl der Mitarbeiter und Gesamtakquisitionen als Prädiktorvariablen und den Jahresumsatz als Antwortvariable verwendet.

Mithilfe des Modells könnten wir dann verstehen, wie stark sich der jährliche Gesamtumsatz (im Durchschnitt) mit jedem zusätzlichen Dollar, der für Werbung ausgegeben wird, jedem zusätzlichen Mitarbeiter und jeder zusätzlichen Akquisition ändert.

Ein Beispiel für eine Vorhersage:

Wir könnten dasselbe multiple lineare Regressionsmodell erstellen und es verwenden, um den Jahresumsatz eines Unternehmens auf der Grundlage seiner gesamten Marketingausgaben, der Anzahl der Mitarbeiter und der gesamten Akquisitionen vorherzusagen.

Beispielsweise könnten wir das Modell verwenden, um den Jahresumsatz eines Unternehmens vorherzusagen, das 25 Millionen US-Dollar für Werbung ausgibt, 40 Mitarbeiter beschäftigt und zwei Akquisitionen getätigt hat.

Zusätzliche Ressourcen

Die folgenden Tutorials bieten zusätzliche Informationen zu wichtigen Begriffen, die es in der Statistik zu verstehen gilt:

Beschreibende oder inferenzielle Statistik: Was ist der Unterschied?
Messniveaus: nominal, ordinal, Intervall und Verhältnis
Qualitative und quantitative Variablen: Was ist der Unterschied?