Schüler-t-test

Von Dr. Benjamin Anderson August 3, 2023 Statistiken Keine Kommentare

In diesem Artikel wird erklärt, was der Student-t-Test ist und wofür er in der Statistik verwendet wird. So erfahren Sie, wie der Student-t-Test durchgeführt wird, welche verschiedenen Arten von Student-t-Tests es gibt und welche Formeln sie jeweils haben.

Was ist der Student-t-Test?

Der Student-T-Test , auch T-Test oder einfach T-Test genannt, ist ein statistischer Test, bei dem die Teststatistik der Student-T-Verteilung folgt. Daher wird in der Statistik der Student-t-Test verwendet, um die Nullhypothese eines Hypothesentests abzulehnen oder zu akzeptieren.

Insbesondere wird der Student-t-Test beim Testen von Hypothesen verwendet, bei denen die untersuchte Grundgesamtheit einer Normalverteilung folgt, die Stichprobengröße jedoch zu klein ist, um die Grundgesamtheitsvarianz zu ermitteln.

Kurz gesagt wird der Student-T-Test verwendet, um die Studienhypothese bestimmter Hypothesentests abzulehnen oder zu akzeptieren. Beispielsweise wird der Student-t-Test verwendet, um Hypothesen für eine Stichprobe, für unabhängige Stichproben oder für verwandte Stichproben zu testen. Wir werden dann sehen, wie der Student-t-Test jeweils berechnet wird.

Arten von Student-T-Tests

Es gibt drei Arten von Student-t-Tests :

Student-T-Test bei einer Stichprobe – wird verwendet, um die Hypothese über den Wert des Stichprobenmittelwerts zu testen.
Student-T-Test für zwei unabhängige Stichproben : Damit können Sie die Hypothese über die Differenz zwischen den Mittelwerten zweier unabhängiger Stichproben testen.
Student-T-Test für zwei gepaarte Stichproben (oder verwandte Stichproben) – wird verwendet, um die Hypothese über den Mittelwert einer zweimal getesteten Stichprobe zu untersuchen.

Ein Beispiel für den Student-t-Test

Hypothesentests für den Stichprobenmittelwert sind solche, bei denen die Nullhypothese und die Alternativhypothese des Tests etwas über den Wert eines Populationsmittelwerts aussagen.

Die Formel für den Student-t-Test bei einer Stichprobe lautet wie folgt:

$\displaystyle t=\frac{\overline{x}-\mu}{\displaystyle \frac{s}{\sqrt{n}}}$

Gold:

$t$

ist die Hypothesenteststatistik für den Mittelwert, der durch die Student-t-Verteilung definiert wird.
$\overline{x}$

ist das Beispielmittel.
$\mu$

ist der Wert des im Hypothesentest vorgeschlagenen Mittelwerts.
$s$

ist die Standardabweichung der Stichprobe.
$n$

ist die Stichprobengröße.

Nachdem der Wert des Student-t-Tests berechnet wurde, muss das Ergebnis des statistischen Tests mit dem kritischen Wert so interpretiert werden, dass die Nullhypothese abgelehnt wird oder nicht:

Wenn der Hypothesentest für den Mittelwert zweiseitig ist, wird die Nullhypothese abgelehnt, wenn der Absolutwert des Student-t-Tests größer als der kritische Wert t _α/2|n-1 ist.
Wenn der Hypothesentest für den Mittelwert mit dem rechten Ende übereinstimmt, wird die Nullhypothese abgelehnt, wenn der Student-t-Testwert größer als der kritische Wert t _α|n-1 ist.
Wenn der Hypothesentest für den Mittelwert mit dem linken Ende übereinstimmt, wird die Nullhypothese abgelehnt, wenn der Student-t-Testwert kleiner als der kritische Wert -t _α|n-1 ist.

$\begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |t|>t_{\alpha/2|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t>t_{\alpha|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t<-t_{\alpha|n-1} \text{ se rechaza } H_0\end{array}$

Beachten Sie, dass die kritischen Testwerte aus der Student-Verteilungstabelle ermittelt werden.

➤ Siehe: Konkretes Beispiel für den Hypothesentest für den Mittelwert

Student-T-Test für unabhängige Stichproben

Der Student-t-Test für unabhängige Stichproben wird verwendet, um die Hypothese einer Beziehung zwischen den Mittelwerten zweier Grundgesamtheiten abzulehnen oder zu akzeptieren, beispielsweise, dass die Mittelwerte zweier Grundgesamtheiten unterschiedlich sind oder dass der Mittelwert von Grundgesamtheit A größer als der Durchschnitt von ist . Bevölkerung B.

Allerdings variiert in diesem Fall die Formel des Student-T-Tests je nachdem, ob die Populationsvarianzen als gleich angenommen werden können oder nicht. Wir werden dann die beiden möglichen Fälle sehen.

Unbekannte und gleiche Abweichungen

Die Formel zur Berechnung des Student-t-Tests für unabhängige Stichproben, wenn die Populationsvarianzen unbekannt sind, aber als gleich angenommen werden, lautet wie folgt:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$

Gold:

$t$

ist die Hypothesenteststatistik für die Mittelwertdifferenz mit unbekannten Varianzen, die einer Student-t-Verteilung mit n ₁ + n ₂ -2 Freiheitsgraden folgt.
$\mu_1$

ist der Mittelwert der Bevölkerung 1.
$\mu_2$

ist der Mittelwert der Bevölkerung 2.
$\overline{x_1}$

ist der Mittelwert von Stichprobe 1.
$\overline{x_2}$

ist der Mittelwert von Stichprobe 2.
$s_p$

ist die gepoolte Standardabweichung.
$n_1$

ist Stichprobengröße 1.
$n_2$

ist Stichprobengröße 2.

Die kombinierte Standardabweichung der beiden Stichproben wird nach folgender Formel berechnet:

$\displaystyle s_p=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}$

Unbekannte und unterschiedliche Variationen

Wenn die Populationsvarianzen unbekannt sind und außerdem davon ausgegangen wird, dass sie unterschiedlich sind, lautet die Formel zur Berechnung des Student-t-Tests für unabhängige Stichproben wie folgt:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle \sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}}$

Gold:

$t$

ist die Hypothesenteststatistik für die Mittelwertdifferenz mit unbekannten Varianzen, die einer Student-t-Verteilung folgt.
$\mu_1$

ist der Mittelwert der Bevölkerung 1.
$\mu_2$

ist der Mittelwert der Bevölkerung 2.
$\overline{x_1}$

ist der Mittelwert von Stichprobe 1.
$\overline{x_2}$

ist der Mittelwert von Stichprobe 2.
$\sigma_1$

ist die Standardabweichung der Grundgesamtheit 1.
$\sigma_2$

ist die Standardabweichung der Grundgesamtheit 2.
$n_1$

ist Stichprobengröße 1.
$n_2$

ist Stichprobengröße 2.

In diesem Fall werden die Freiheitsgrade der Student-t-Verteilung jedoch anhand der folgenden Formel berechnet:

$\displaystyle GL=\frac{\displaystyle\left(\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}\right)^2}{\displaystyle\frac{\displaystyle\frac{s_1^2}{n_1}}{n_1-1}+\frac{\displaystyle\frac{s_2^2}{n_2}}{n_2-1}}$

➤ Siehe: Konkretes Beispiel für den Hypothesentest zur Mittelwertdifferenz

Student-T-Test für gepaarte oder verwandte Stichproben

Dieser Test wird verwendet, wenn zwei untersuchte Proben miteinander in Beziehung stehen, sodass es sich tatsächlich um eine einzelne Stichprobe von Personen handelt, die zweimal analysiert wurde (jedes Mal unter unterschiedlichen Bedingungen).

Sie können beispielsweise die Noten der Studierenden in einem Mathematik- und Statistikkurs analysieren, um festzustellen, ob zwischen den Durchschnittswerten der beiden Fächer ein signifikanter Unterschied besteht. In diesem Fall ist die Mathematiknote jedes Schülers mit der Statistiknote desselben Schülers verknüpft.

Die Student-T-Testformel für gepaarte oder verwandte Stichproben lautet:

$\displaystyle t=\frac{\overline{x_D}-\mu_D}{\displaystyle \frac{s_D}{\sqrt{n}}}$

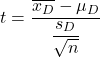
Gold:

$t$

ist die Hypothesenteststatistik für gepaarte Mittelwerte, die durch die Student-t-Verteilung definiert wird.
$\overline{x_D}$

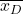
ist der Mittelwert der Stichprobe, der aus der Differenz der Daten gebildet wird.
$\mu_D$

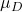
ist der Wert des im Hypothesentest vorgeschlagenen Mittelwerts.
$s_D$

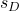
ist die Standardabweichung der Stichprobe, die sich aus der Differenz der Daten ergibt.
$n$

ist die Stichprobengröße.

T-Test-Annahmen des Schülers

Um den Student-t-Test durchführen zu können, müssen folgende Bedingungen erfüllt sein:

Kontinuität – Probendaten sind kontinuierlich.
Zufälligkeit : Die Datenproben wurden zufällig ausgewählt.
Homogenität : Die Varianz der Datenstichprobe ist homogen.
Normalität – Die Verteilung, die die Datenstichprobe definiert, ist annähernd normal.

So führen Sie einen Student-T-Test durch

Abschließend werden zusammenfassend die Schritte beschrieben, die zur Durchführung eines Student-t-Tests zu befolgen sind.

Definieren Sie die Null- und Alternativhypothese des Hypothesentests.
Legen Sie das Signifikanzniveau (α) des Hypothesentests fest.
Stellen Sie sicher, dass die Annahmen des Student-t-Tests erfüllt sind.
Wenden Sie die entsprechende Student-T-Testformel an und berechnen Sie die Teststatistik.
Interpretieren Sie das Ergebnis des Student-t-Tests, indem Sie es mit dem kritischen Wert des Tests vergleichen.

Über den Autor

Dr. Benjamin Anderson

Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen

Was ist der Student-t-Test?

Arten von Student-T-Tests

Ein Beispiel für den Student-t-Test

Student-T-Test für unabhängige Stichproben

Unbekannte und gleiche Abweichungen

Unbekannte und unterschiedliche Variationen

Student-T-Test für gepaarte oder verwandte Stichproben

T-Test-Annahmen des Schülers

So führen Sie einen Student-T-Test durch

Über den Autor

Dr. Benjamin Anderson

Einen Kommentar hinzufügen