Kreisdiagramme

In diesem Artikel wird erklärt, was Kreisdiagramme sind, wie man ein Kreisdiagramm erstellt und außerdem können Sie sich eine Schritt-für-Schritt-Anleitung für diese Art von statistischem Diagramm ansehen.

Was ist ein Kreisdiagramm?

Ein Kreisdiagramm oder Tortendiagramm ist eine Art statistisches Diagramm, in dem Daten durch einen Kreis dargestellt werden, der in Sektoren unterteilt ist, sodass der Winkel jedes Sektors proportional zu seiner entsprechenden Häufigkeit ist.

Mit anderen Worten: Je häufiger ein Wert vorkommt, desto größer ist der entsprechende Sektor im Diagramm.

Daher werden Kreisdiagramme verwendet, um die Häufigkeit jedes Werts visuell zu analysieren. In der Statistik werden solche Diagramme hauptsächlich zur Darstellung qualitativer Variablen verwendet.

So erstellen Sie ein Kreisdiagramm

Die Schritte zum Erstellen eines Kreisdiagramms sind wie folgt:

1. Sammeln Sie statistische Daten von der Probe, die Sie analysieren möchten, und erstellen Sie die Häufigkeitstabelle.
2. Berechnen Sie den Winkel jedes Sektors des Diagramms . Dazu müssen Sie die folgende Formel verwenden:



Gold



ist der Winkel des Sektors i ,



seine absolute Häufigkeit und



die Gesamtzahl der Daten.

3. Stellen Sie anhand der berechneten Winkel die Sektoren mithilfe eines Winkelmessers in einem kreisförmigen Diagramm dar.
4. Berechnen Sie den Prozentsatz jedes Sektors im Diagramm mithilfe der folgenden Formel:



Gold



ist der Prozentsatz des Sektors i ,



seine absolute Häufigkeit und



die Gesamtzahl der Daten.

5. Geben Sie im Diagramm den Prozentsatz jedes Sektors an.

Beispiel für ein Kreisdiagramm

Damit Sie genau sehen können, wie Sie ein Kreisdiagramm erstellen, finden Sie unten ein Schritt-für-Schritt-Beispiel:

• 50 Personen wurden nach ihrer Lieblingsstadt befragt und die Daten in der folgenden Tabelle zusammengestellt. Stellen Sie diese statistischen Daten in einem Kreisdiagramm dar.

Zunächst müssen wir den Winkel berechnen, der jedem Sektor entspricht, daher verwenden wir für jeden Wert die folgende Formel:

Die Berechnung des Winkels des Sektors, der dem ersten Wert entspricht, lautet beispielsweise:

Und dann zeichnen wir in einem Kreis den Sektor, der dem mit einem Winkelmesser berechneten Winkel entspricht:

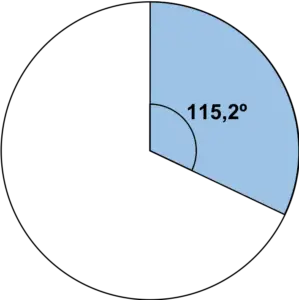
Wir wiederholen den gleichen Vorgang für alle Werte:

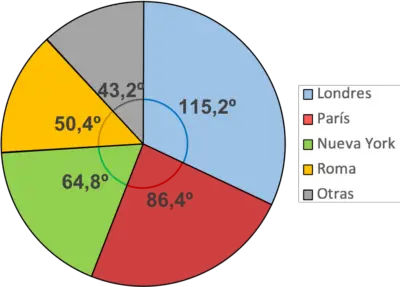
Es wird empfohlen, jeden Sektor in einer anderen Farbe zu lackieren, um die Unterscheidung zu erleichtern. Ebenso sollte eine Legende hinzugefügt werden, um die Bedeutung jeder Farbe anzugeben.

Sobald alle Sektoren vertreten sind, muss der entsprechende Prozentsatz berechnet werden. Dazu wenden wir die folgende Formel an:

Der Prozentsatz jedes Sektors beträgt daher:

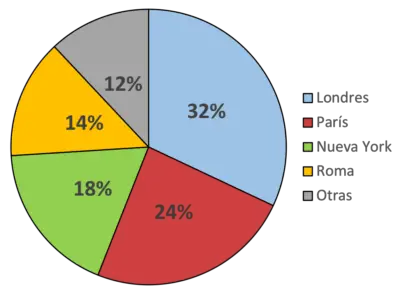
Mit diesem Diagramm zeigen wir an, dass beispielsweise die Farbe Blau die Stadt London darstellt, die Stadt, die die meisten Menschen mögen (32 % der Menschen). Ebenso steht die Farbe Grün für New York, die Lieblingsstadt von 18 % der Befragten.

Vor- und Nachteile von Kreisdiagrammen

Aufgrund ihrer Eigenschaften haben Kreisdiagramme folgende Vor- und Nachteile:

Vorteil:

• Dabei handelt es sich um ein sehr anschauliches statistisches Diagramm, mit dem Sie schnell analysieren und Schlussfolgerungen ziehen können.
• Es ist sehr nützlich für die grafische Darstellung qualitativer Daten.
• Wenn dies mit einem Computer, zum Beispiel mit Excel, erledigt wird, geht es sehr schnell.

Nachteile:

• Wenn das Diagramm viele verschiedene Sektoren enthält, kann das Lesen des Diagramms kompliziert werden. In diesem Fall wird empfohlen, die kleinen Sektoren in einem einzigen Sektor mit der Bezeichnung „Andere“ zusammenzufassen.
• Es gibt andere Arten statistischer Diagramme, die sich besser für die Darstellung quantitativer Variablen oder Zeitreihen eignen.