Sich gegenseitig einschließende oder sich gegenseitig ausschließende ereignisse

Zwei Ereignisse schließen sich gegenseitig aus, wenn sie nicht gleichzeitig auftreten können.

Angenommen, Ereignis A ist das Ereignis, bei dem ein Würfel auf einer geraden Zahl landet, und Ereignis B ist das Ereignis, bei dem ein Würfel auf einer ungeraden Zahl landet.

Wir würden den Beispielraum für Ereignisse wie folgt definieren:

• A = {2, 4, 6}
• B = {1, 3, 5}

Beachten Sie, dass es keine Überlappung zwischen den beiden abgetasteten Räumen gibt. Die Ereignisse A und B schließen sich also gegenseitig aus, da sie nicht beide gleichzeitig auftreten können. Die Zahl, auf die ein Würfel fällt, darf nicht sowohl gerade als auch ungerade sein.

Umgekehrt schließen sich zwei Ereignisse gegenseitig ein, wenn sie gleichzeitig auftreten können .

Beispiel: Ereignis C sei das Ereignis, bei dem ein Würfel auf einer geraden Zahl landet, und Ereignis D sei das Ereignis, bei dem ein Würfel auf einer Zahl größer als 3 landet.

Wir würden den Beispielraum für Ereignisse wie folgt definieren:

• C = {2, 4, 6}
• d = {4, 5, 6}

Beachten Sie, dass es eine Überlappung zwischen den beiden abgetasteten Räumen gibt. Somit schließen sich die Ereignisse C und D gegenseitig ein, da sie gleichzeitig auftreten können. Es ist möglich, dass die Würfel auf einer geraden Zahl größer als 3 landen.

Ereigniswahrscheinlichkeiten

Wenn sich zwei Ereignisse gegenseitig ausschließen, ist die Wahrscheinlichkeit, dass beide eintreten, Null.

Betrachten Sie beispielsweise die beiden Beispielräume für die Ereignisse A und B oben:

• A = {2, 4, 6}
• B = {1, 3, 5}

Da es in den Probenräumen keine Überlappung gibt, würden wir sagen: P(A und B) = 0 .

Wenn sich jedoch zwei Ereignisse gegenseitig einschließen , ist die Wahrscheinlichkeit, dass beide auftreten, eine Zahl größer als Null.

Betrachten Sie beispielsweise die beiden Beispielräume für die Ereignisse C und D zuvor:

• C = {2, 4, 6}
• d = {4, 5, 6}

Da es 6 mögliche Zahlen gibt, auf denen die Würfel landen könnten, und zwei dieser Zahlen (4 und 6) zu den beiden Ereignissen C und D gehören, würden wir P(C und D) als 2/6 oder 1/3 berechnen.

Sehen Sie sich gegenseitig einschließende und sich gegenseitig ausschließende Ereignisse an

Wir verwenden häufig Venn-Diagramme, um die mit Ereignissen verbundenen Wahrscheinlichkeiten zu visualisieren.

Wenn sich zwei Ereignisse gegenseitig ausschließen, überlappen sie sich in einem Venn-Diagramm überhaupt nicht:

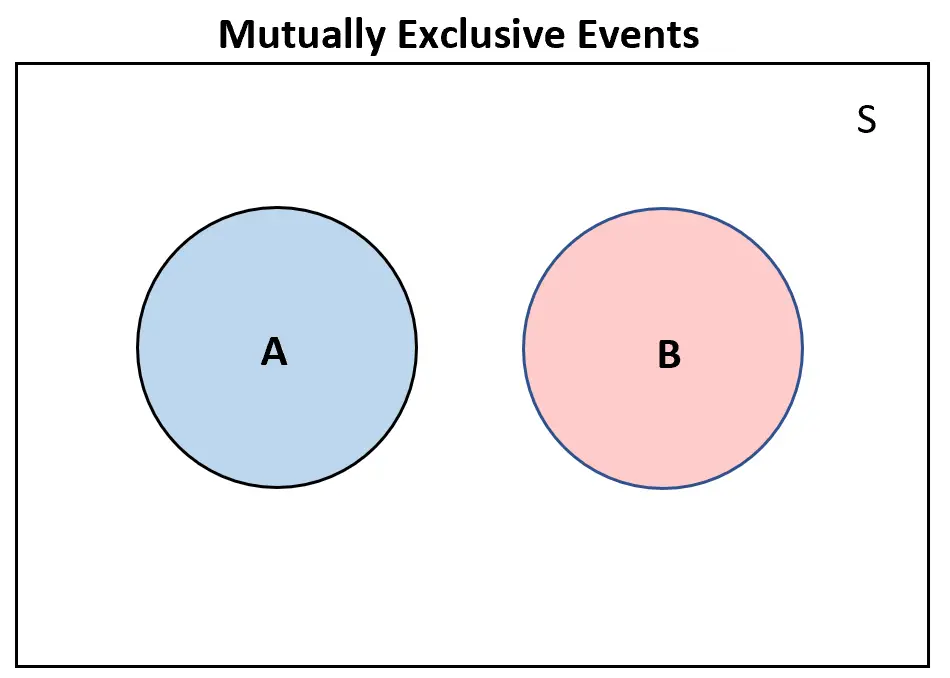
Wenn sich umgekehrt zwei Ereignisse gegenseitig einschließen , gäbe es im Venn-Diagramm zumindest eine gewisse Überlappung:

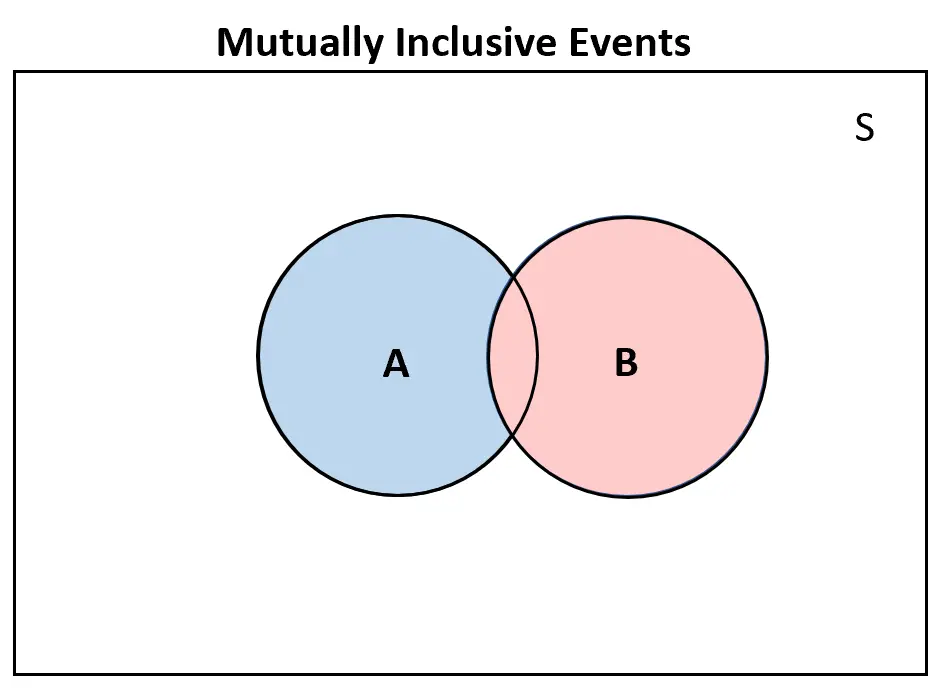
Zusätzliche Ressourcen

Eine Einführung in die theoretische Wahrscheinlichkeit
Die allgemeine Regel der Multiplikation
Was sind disjunkte Ereignisse?