Wie ist sig zu interpretieren? werte (zweiseitig) in spss
Wenn Sie statistische Tests in SPSS durchführen, enthält die Ausgabetabelle häufig ein Sig. Wert (bilateral) .
Dieser Wert stellt den zweiseitigen p-Wert des Tests dar.
Wenn dieser Wert unter Ihrem Signifikanzniveau liegt (übliche Optionen sind 0,05 oder 0,01), können Sie die Nullhypothese Ihres Tests ablehnen .
Dieses Tutorial enthält Beispiele für die Interpretation von Sig. (zweiseitiger) Wert verschiedener statistischer Tests.
Beispiel 1: T-Test bei einer Stichprobe
Ein T-Test bei einer Stichprobe wird verwendet, um zu testen, ob der Mittelwert einer Grundgesamtheit einem bestimmten Wert entspricht oder nicht.
Angenommen, ein Botaniker möchte wissen, ob die durchschnittliche Höhe einer bestimmten Pflanzenart 15 Zoll beträgt. Sie entnimmt eine Zufallsstichprobe von 12 Pflanzen und notiert deren Höhe in Zoll.
Anschließend wird diese Stichprobe verwendet, um einen t-Test bei einer Stichprobe mit den folgenden Null- und Alternativhypothesen durchzuführen:
- H 0 : μ = 15 (der reale Bevölkerungsmittelwert beträgt 15 Zoll)
- H A : μ ≠ 15 (der tatsächliche Bevölkerungsdurchschnitt beträgt nicht 15 Zoll)
Sie führt diesen T-Test bei einer Stichprobe in SPSS durch und erhält die folgenden Ergebnisse:
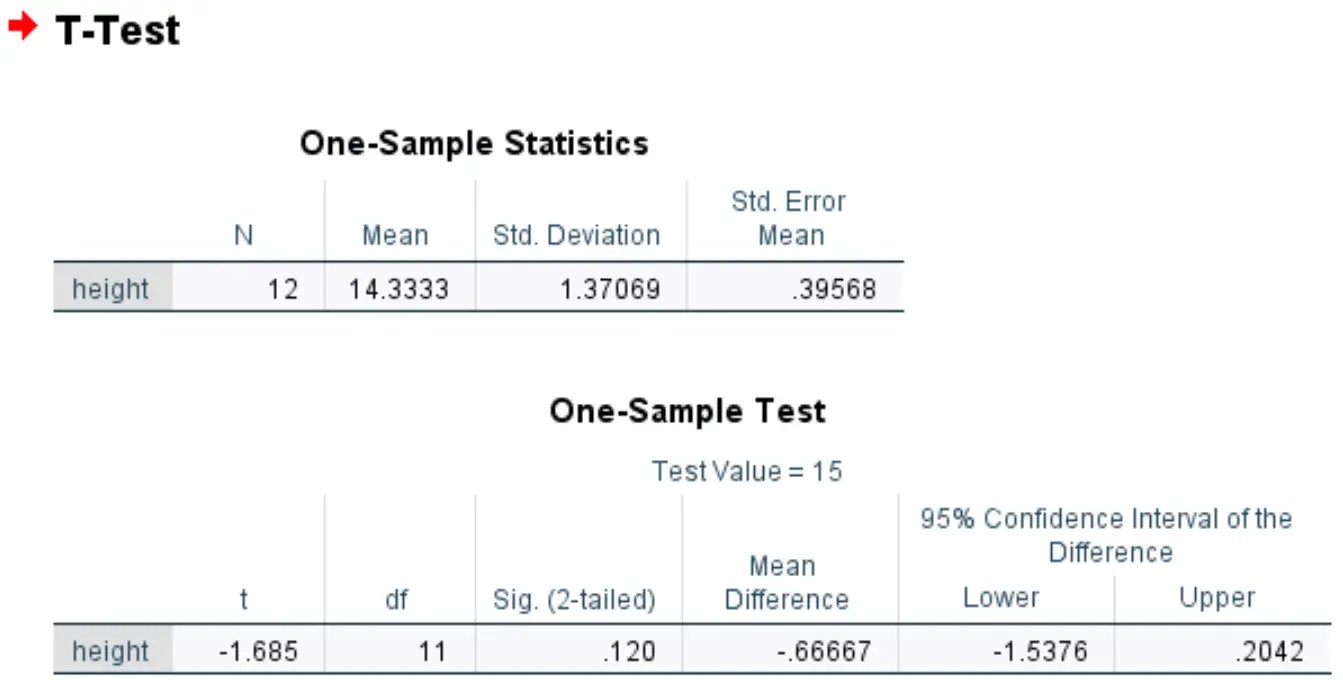
Die Sig. Der Wert (zweiseitig) beträgt 0,120 .
Dies stellt den zweiseitigen p-Wert dar, der einem Wert von -1,685 mit 11 Freiheitsgraden entspricht.
Da der p-Wert des Tests (0,120) nicht kleiner als 0,05 ist, können wir die Nullhypothese nicht ablehnen.
Mit anderen Worten: Wir haben nicht genügend Beweise dafür, dass die tatsächliche durchschnittliche Höhe dieser Pflanzenart etwas anderes als 15 Zoll beträgt.
Beispiel 2: T-Test bei zwei Stichproben
Ein T-Test mit zwei Stichproben wird verwendet, um zu testen, ob die Mittelwerte zweier Populationen gleich sind oder nicht.
Angenommen, Forscher möchten wissen, ob eine neue Kraftstoffaufbereitung zu einer Änderung des durchschnittlichen Kilometerstands pro Gallone eines bestimmten Autos führt. Um dies zu testen, führen sie ein Experiment durch, bei dem 12 Autos die neue Kraftstoffaufbereitung erhalten und 12 Autos nicht.
Forscher führen einen T-Test bei zwei Stichproben mit den folgenden Null- und Alternativhypothesen durch:
- H 0 : μ 1 = μ 2 (der durchschnittliche MPG zwischen den beiden Populationen ist gleich)
- H 1 : μ 1 ≠ μ 2 (der durchschnittliche MPG zwischen den beiden Populationen ist nicht gleich)
Sie führen einen T-Test bei zwei Stichproben in SPSS durch und erhalten die folgenden Ergebnisse:
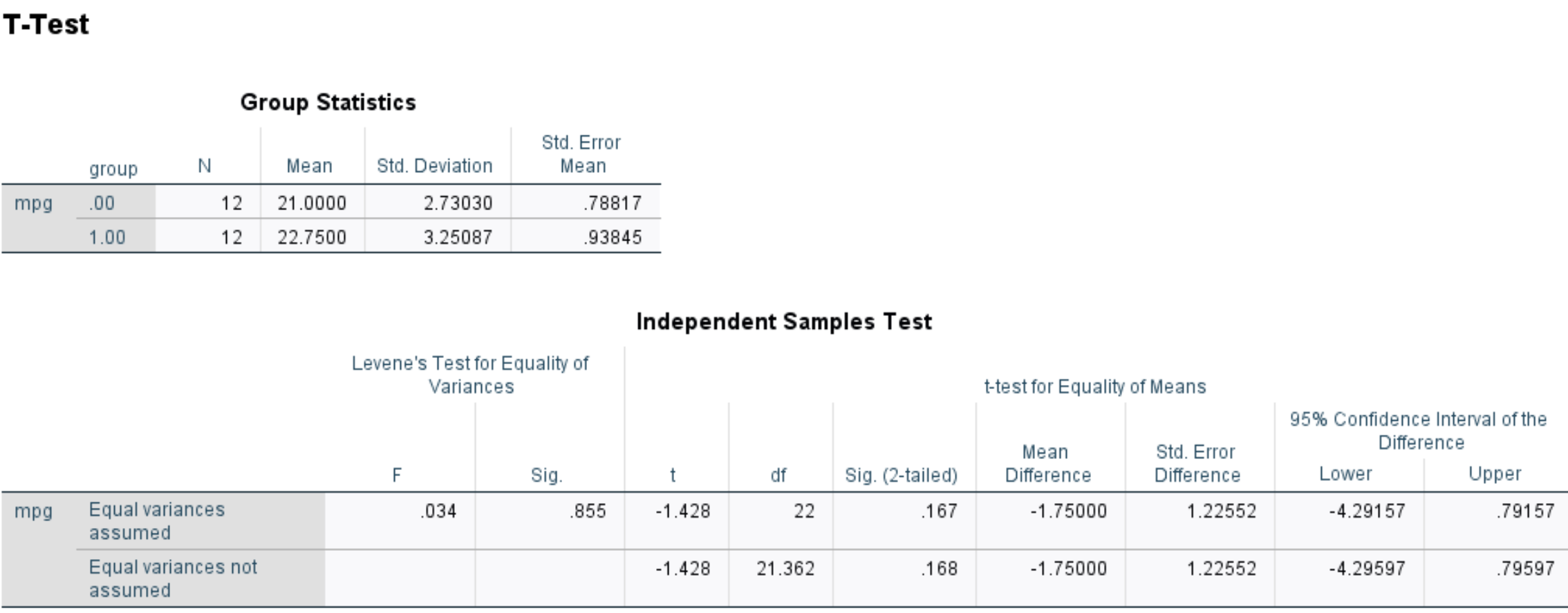
Die Sig. Der Wert (2-seitig) beträgt 0,167 .
Dies stellt den zweiseitigen p-Wert dar, der einem Wert von -1,428 mit 22 Freiheitsgraden entspricht.
Da der p-Wert des Tests (0,167) nicht kleiner als 0,05 ist, können wir die Nullhypothese nicht ablehnen.
Mit anderen Worten: Wir haben nicht genügend Beweise, um zu sagen, dass der tatsächliche durchschnittliche Kraftstoffverbrauch zwischen Autos, die eine Behandlung erhalten, und solchen, die keine Behandlung erhalten, unterschiedlich ist.
Zusätzliche Ressourcen
Die folgenden Tutorials erklären, wie Sie verschiedene statistische Tests in SPSS durchführen:
So führen Sie einen T-Test bei einer Stichprobe in SPSS durch
So führen Sie einen T-Test bei zwei Stichproben in SPSS durch
So führen Sie einen T-Test für gepaarte Stichproben in SPSS durch
Über den Autor
Dr. Benjamin Anderson
Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen