So testen sie die signifikanz einer regressionssteigung

Nehmen wir an, wir haben den folgenden Datensatz, der die Quadratmeterzahl und den Preis von 12 verschiedenen Häusern zeigt:

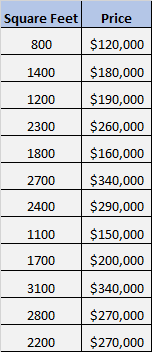
Wir möchten wissen, ob ein signifikanter Zusammenhang zwischen Quadratmeterzahl und Preis besteht.

Um eine Vorstellung davon zu bekommen, wie die Daten aussehen, erstellen wir zunächst ein Streudiagramm mit Quadratfuß auf der x-Achse und dem Preis auf der y-Achse:

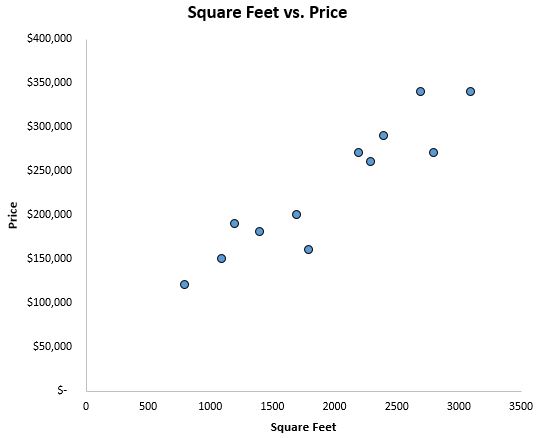
Wir können deutlich erkennen, dass es einen positiven Zusammenhang zwischen Quadratmeterzahl und Preis gibt. Mit zunehmender Quadratmeterzahl steigt tendenziell auch der Preis des Hauses.

Um jedoch herauszufinden, ob ein statistisch signifikanter Zusammenhang zwischen Quadratmeterzahl und Preis besteht, müssen wir eine einfache lineare Regression durchführen.

Wir führen also eine einfache lineare Regression mit Quadratfuß als Prädiktor und dem Preis als Antwort durch und erhalten das folgende Ergebnis:

Unabhängig davon, ob Sie eine einfache lineare Regression in Excel, SPSS, R oder einer anderen Software ausführen, erhalten Sie ein Ergebnis, das dem oben gezeigten ähnelt.

Denken Sie daran, dass eine einfache lineare Regression die Gerade der besten Anpassung ergibt, also die Gleichung der Geraden, die am besten zu den Daten in unserem Streudiagramm „passt“. Diese Best-Fit-Linie ist definiert als:

ŷ = b ₀ + b ₁ x

Dabei ist ŷ der vorhergesagte Wert der Antwortvariablen, b ₀ der Achsenabschnitt, b ₁ der Regressionskoeffizient und x der Wert der Prädiktorvariablen.

Der Wert von b ₀ wird durch den Koeffizienten des Ursprungs angegeben, der 47588,70 beträgt.

Der Wert von b ₁ wird durch den Koeffizienten der Prädiktorvariablen Quadratfuß angegeben, der 93,57 beträgt.

Die am besten geeignete Gerade in diesem Beispiel ist also ŷ = 47588,70+ 93,57x

So interpretieren Sie diese Best-Fit-Linie:

• b ₀ : Wenn der Wert von Quadratfuß Null ist, beträgt der erwartete Durchschnittspreis 47.588,70 $. (In diesem Fall ist es nicht wirklich sinnvoll, den Achsenabschnitt zu interpretieren, da ein Haus niemals null Quadratmeter groß sein kann.)
• b ₁ : Für jeden zusätzlichen Quadratfuß beträgt die durchschnittliche erwartete Preissteigerung 93,57 $.

Wir wissen also, dass für jeden zusätzlichen Quadratfuß ein durchschnittlicher Preisanstieg von 93,57 US-Dollar zu erwarten ist.

Um zu wissen, ob dieser Anstieg statistisch signifikant ist, müssen wir einen Hypothesentest für B ₁ durchführen oder ein Konfidenzintervall für B ₁ erstellen.

Hinweis : Ein Hypothesentest und ein Konfidenzintervall liefern immer die gleichen Ergebnisse.

Konstruktion eines Konfidenzintervalls für eine Regressionssteigung

Um ein Konfidenzintervall für eine Regressionssteigung zu erstellen, verwenden wir die folgende Formel:

Konfidenzintervall = b ₁ +/- (t _{1-∝/2, n-2} ) * (Standardfehler von b ₁ )

Gold:

• b ₁ ist der im Regressionsergebnis angegebene Steigungskoeffizient
• (t _{1-∝/2, n-2} ) ist der kritische t-Wert für das 1-∝-Konfidenzniveau mit n-2 Freiheitsgraden, wobei n die Gesamtzahl der Beobachtungen in unserem Datensatz ist
• (Standardfehler von b ₁ ) ist der im Regressionsergebnis angegebene Standardfehler von b ₁

Für unser Beispiel erfahren Sie hier, wie Sie ein 95 %-Konfidenzintervall für B ₁ erstellen:

• b ₁ ist 93,57 aus der Regressionsausgabe.
• Da wir ein 95 %-Konfidenzintervall verwenden, ∝ = 0,05 und n-2 = 12-2 = 10, also t _{0,975, ist 10} gemäß der t-Verteilungstabelle 2,228
• (der Standardfehler von _b1 ) beträgt 11,45 aus der Regressionsausgabe

Somit ist unser 95 %-Konfidenzintervall für B ₁ :

93,57 +/- (2,228) * (11,45) = (68,06, 119,08)

Dies bedeutet, dass wir zu 95 % davon überzeugt sind, dass der tatsächliche durchschnittliche Preisanstieg für jeden zusätzlichen Quadratfuß zwischen 68,06 und 119,08 US-Dollar liegt.

Beachten Sie, dass 0 $ nicht in diesem Intervall liegt, sodass die Beziehung zwischen Quadratmeterzahl und Preis bei einem Konfidenzniveau von 95 % statistisch signifikant ist.

Durchführen eines Hypothesentests für eine Regressionssteigung

Um einen Hypothesentest für eine Regressionssteigung durchzuführen, befolgen wir die fünf Standardschritte für jeden Hypothesentest :

Schritt 1. Formulieren Sie die Hypothesen.

Die Nullhypothese (H0): B ₁ = 0

Die Alternativhypothese: (Ha): B ₁ ≠ 0

Schritt 2: Bestimmen Sie ein zu verwendendes Signifikanzniveau.

Da wir im vorherigen Beispiel ein Konfidenzintervall von 95 % erstellt haben, verwenden wir hier den entsprechenden Ansatz und wählen ein Signifikanzniveau von 0,05.

Schritt 3. Finden Sie die Teststatistik und den entsprechenden p-Wert.

In diesem Fall ist die Teststatistik t = Koeffizient von b ₁ / Standardfehler von b ₁ mit n-2 Freiheitsgraden. Diese Werte können wir aus dem Regressionsergebnis ermitteln:

Somit beträgt die Teststatistik t = 92,89 / 13,88 = 6,69.

Unter Verwendung des T-Score-zu-P-Wert-Rechners mit einem Score von 6,69 mit 10 Freiheitsgraden und einem zweiseitigen Test beträgt der p-Wert = 0,000 .

Schritt 4. Lehnen Sie die Nullhypothese ab oder lehnen Sie sie nicht ab.

Da der p-Wert unter unserem Signifikanzniveau von 0,05 liegt, lehnen wir die Nullhypothese ab.

Schritt 5. Interpretieren Sie die Ergebnisse.

Da wir die Nullhypothese abgelehnt haben, haben wir genügend Beweise dafür, dass der tatsächliche durchschnittliche Preisanstieg für jeden zusätzlichen Quadratfuß nicht Null ist.