So führen sie den friedman-test in excel durch

Der Friedman-Test ist eine nichtparametrische Alternative zur ANOVA mit wiederholten Messungen . Es wird verwendet, um zu bestimmen, ob ein statistisch signifikanter Unterschied zwischen den Mittelwerten von drei oder mehr Gruppen besteht, in denen in jeder Gruppe dieselben Probanden vorkommen.

In diesem Tutorial wird erklärt, wie Sie den Friedman-Test in Excel durchführen.

Beispiel: der Friedman-Test in Excel

Befolgen Sie die folgenden Schritte, um den Friedman-Test in Excel durchzuführen.

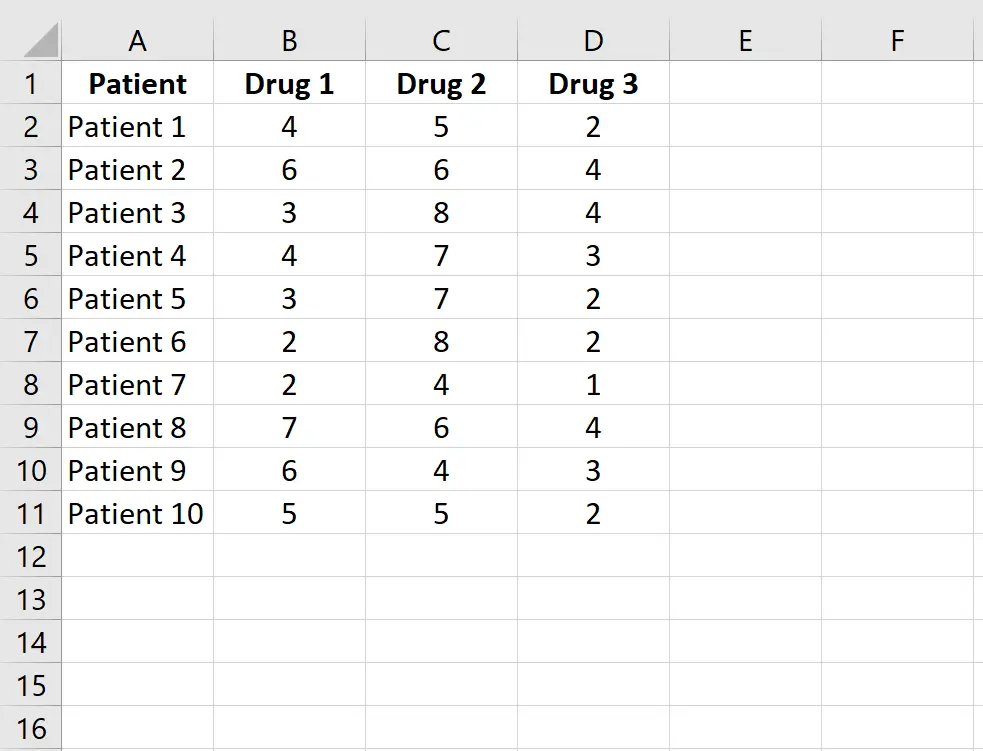
Schritt 1: Geben Sie die Daten ein.

Geben Sie die folgenden Daten ein, die die Reaktionszeit (in Sekunden) von 10 Patienten zeigen, die drei verschiedene Medikamente einnehmen. Da bei jedem Patienten jedes der drei Medikamente gemessen wird, verwenden wir den Friedman-Test, um festzustellen, ob sich die durchschnittliche Reaktionszeit zwischen den Medikamenten unterscheidet.

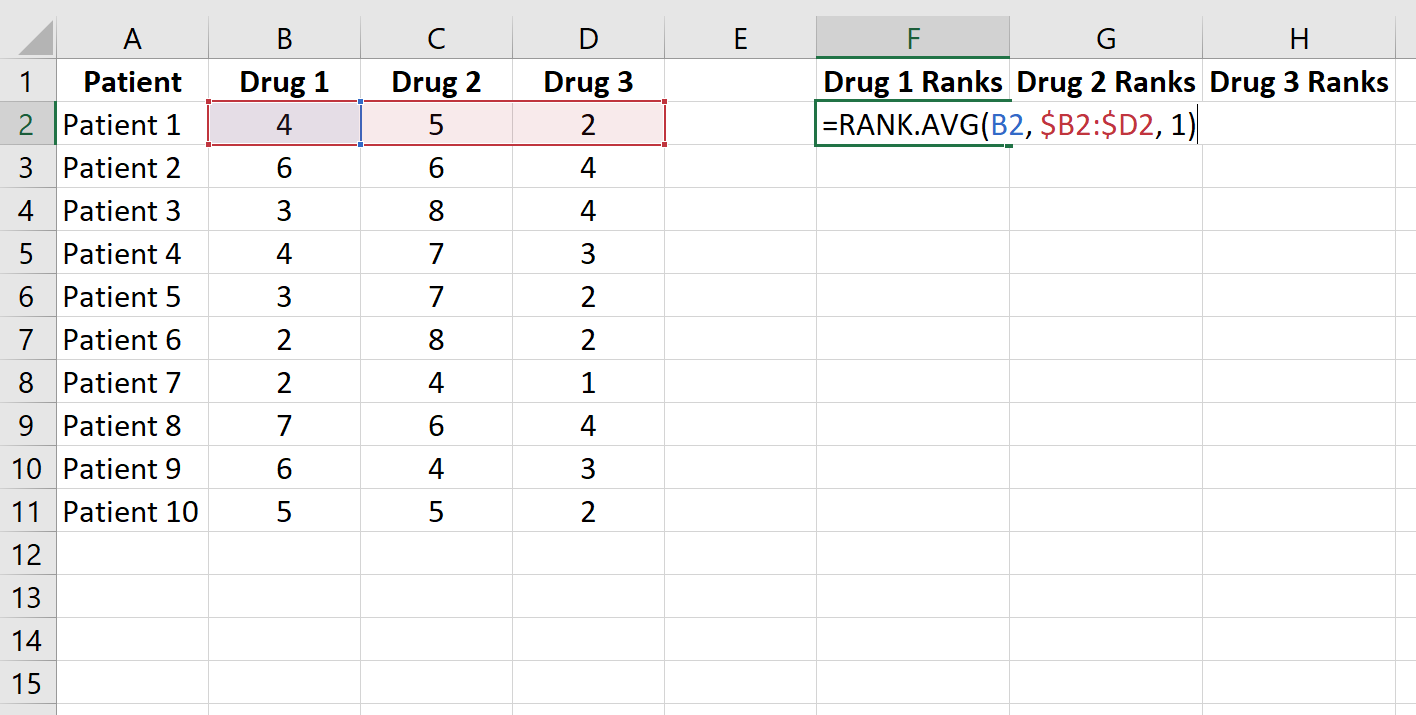
Schritt 2: Klassifizieren Sie die Daten.

Ordnen Sie als Nächstes die Datenwerte in jeder Zeile mit der Funktion =RANK.AVG() in aufsteigender Reihenfolge. Die folgende Formel zeigt, wie der Rang der Reaktionszeit von Patient 1 auf Medikament 1 berechnet wird:

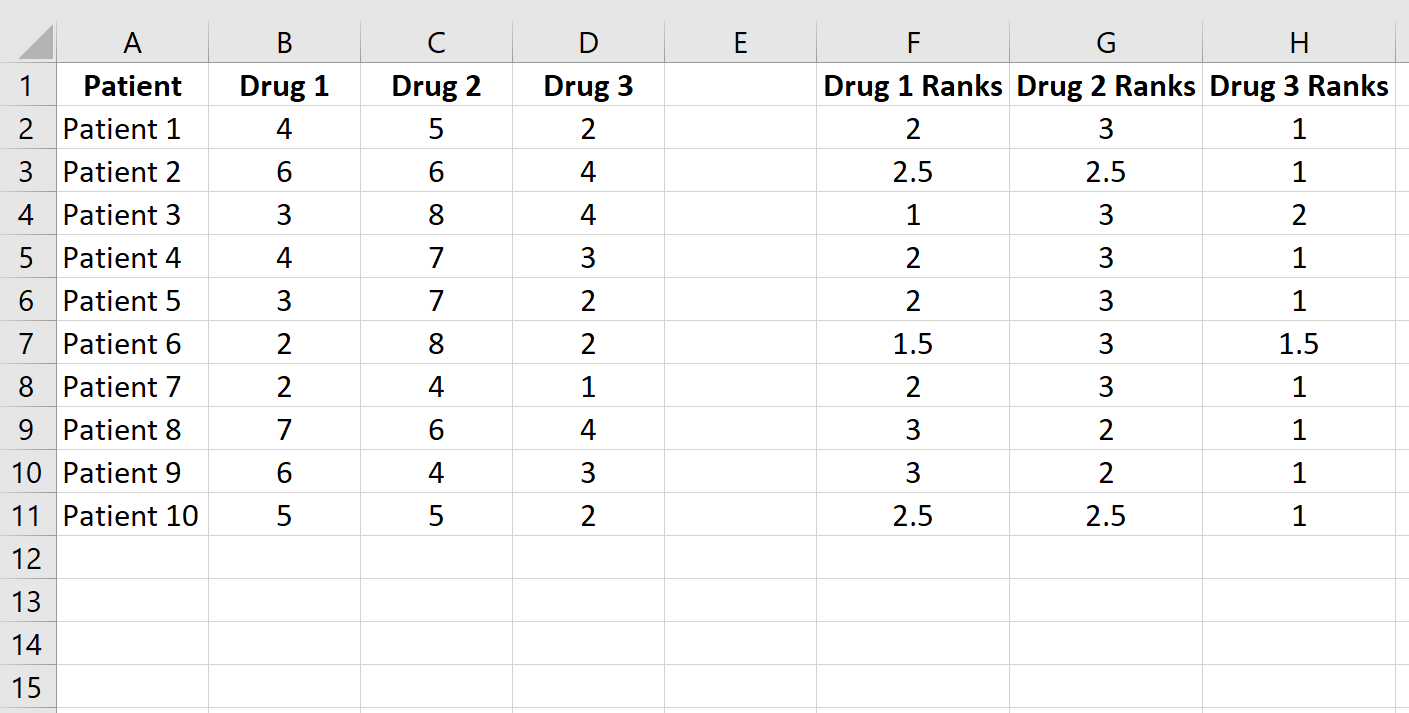
Kopieren Sie diese Formel in die restlichen Zellen:

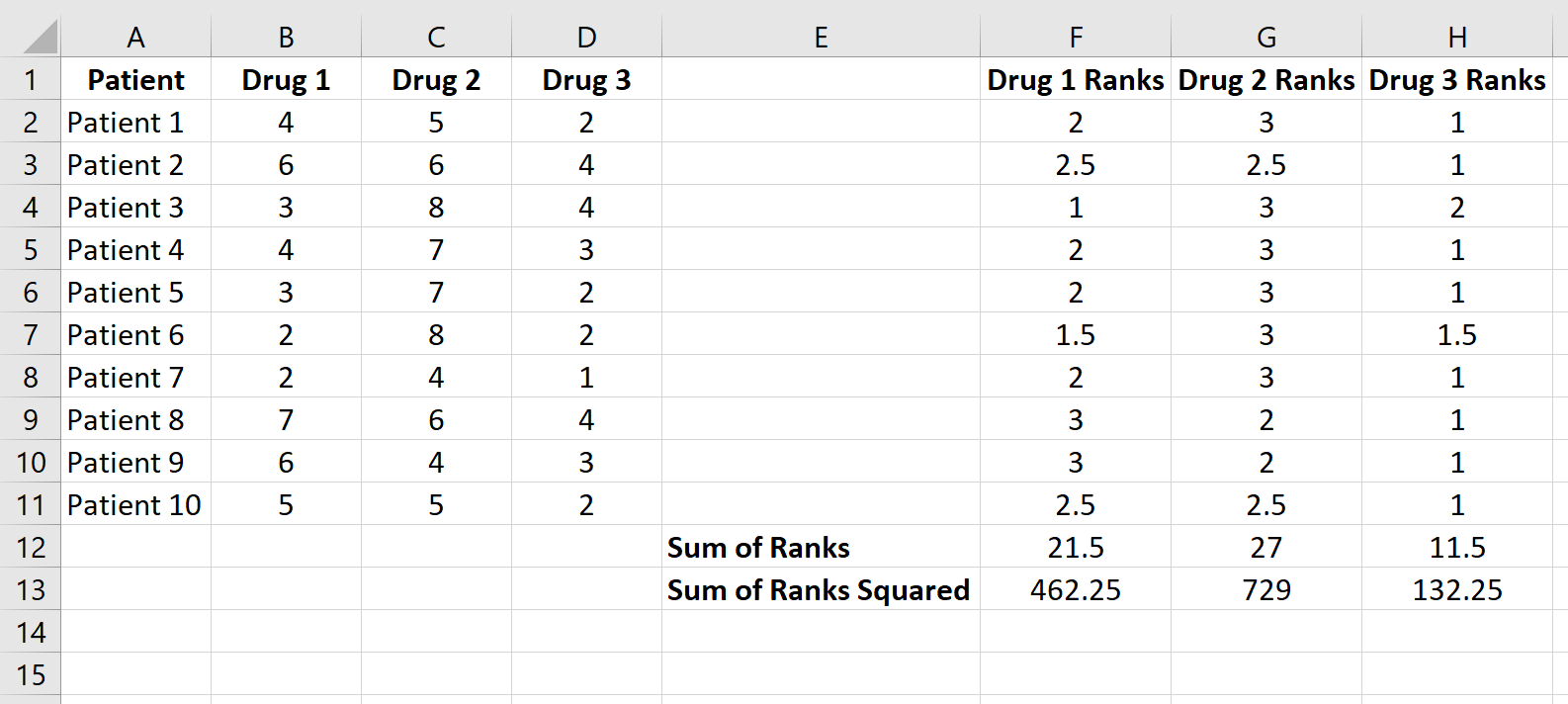
Berechnen Sie als Nächstes die Summe der Ränge für jede Spalte sowie die quadrierte Summe der Ränge:

Schritt 3: Berechnen Sie die Teststatistik und den entsprechenden p-Wert.

Die Teststatistik ist definiert als:

Q = 12/nk(k+1) * ΣR _j ² – 3n(k+1)

Gold:

• n = Anzahl der Patienten
• k = Anzahl der Behandlungsgruppen
• R _j ² = Summe der Ränge für die ^j-te Gruppe

Unter der Nullhypothese folgt Q einer Chi-Quadrat-Verteilung mit k-1 Freiheitsgraden.

Der folgende Screenshot zeigt die Formeln zur Berechnung der Teststatistik Q und des entsprechenden p-Werts:

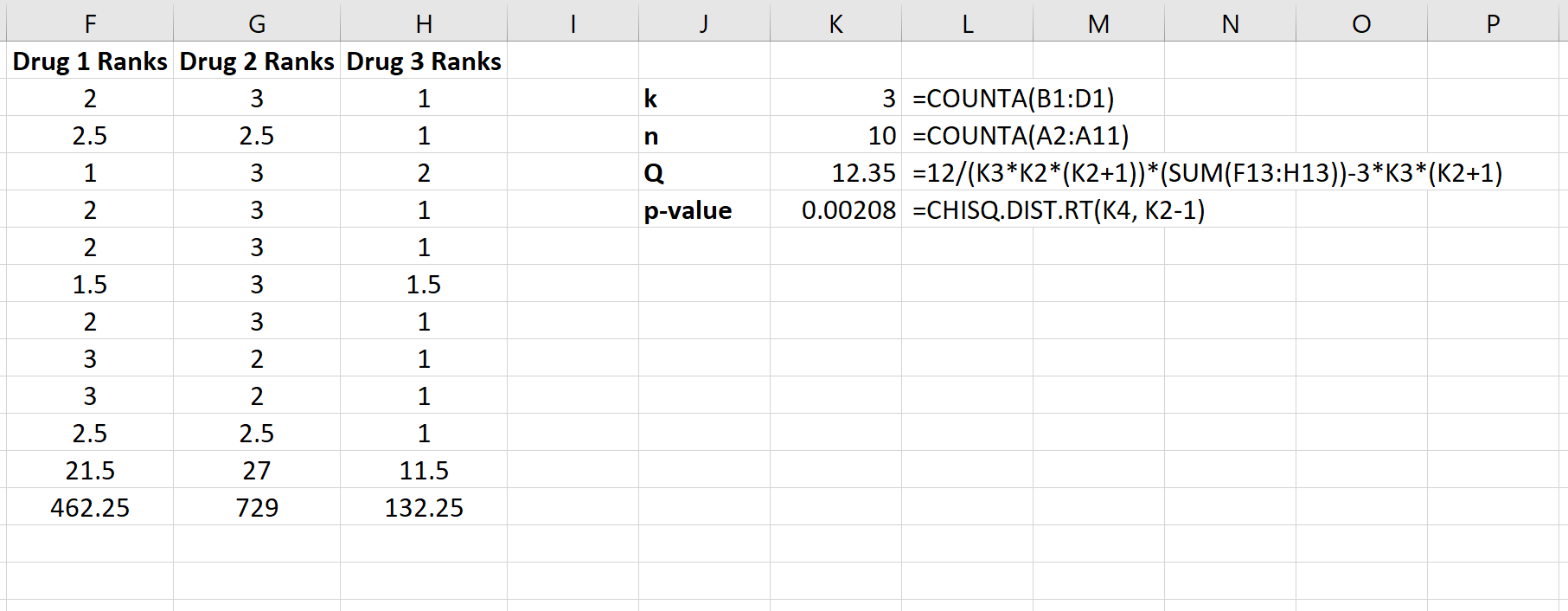
Die Teststatistik ist Q = 12,35 und der entsprechende p-Wert ist p = 0,00208 . Da dieser Wert kleiner als 0,05 ist, können wir die Nullhypothese zurückweisen, dass die durchschnittliche Reaktionszeit für alle drei Medikamente gleich ist. Wir haben genügend Beweise, um zu dem Schluss zu kommen, dass die Art der verwendeten Medikamente zu statistisch signifikanten Unterschieden in der Reaktionszeit führt.

Schritt 4: Melden Sie die Ergebnisse.

Abschließend möchten wir Ihnen die Testergebnisse mitteilen. Hier ist ein Beispiel dafür:

An 10 Patienten wurde ein Friedman-Test durchgeführt, um die Wirkung von drei verschiedenen Medikamenten auf die Reaktionszeit zu untersuchen. Jeder Patient verwendete jedes Medikament einmal.

Die Ergebnisse zeigten, dass die Art der verwendeten Medikamente zu statistisch signifikanten Unterschieden in der Reaktionszeit führte (Q = 12,35, p = 0,00208).