So führen sie eine spline-regression in r durch (mit beispiel)

Die Spline-Regression ist ein Regressionstyp, der verwendet wird, wenn es Punkte oder „Knoten“ gibt, an denen sich das Muster in den Daten abrupt ändert und die lineare Regression und die polynomielle Regression nicht flexibel genug sind, um an die Daten anzupassen.

Das folgende Schritt-für-Schritt-Beispiel zeigt, wie eine Spline-Regression in R durchgeführt wird.

Schritt 1: Erstellen Sie die Daten

Lassen Sie uns zunächst einen Datensatz in R mit zwei Variablen erstellen und ein Streudiagramm erstellen, um die Beziehung zwischen den Variablen zu visualisieren:

 #create data frame
df <- data. frame (x=1:20,
                 y=c(2, 4, 7, 9, 13, 15, 19, 16, 13, 10,
                     11, 14, 15, 15, 16, 15, 17, 19, 18, 20))

#view head of data frame
head(df)

  xy
1 1 2
2 2 4
3 3 7
4 4 9
5 5 13
6 6 15

#create scatterplot
plot(df$x, df$y, cex= 1.5 , pch= 19 )

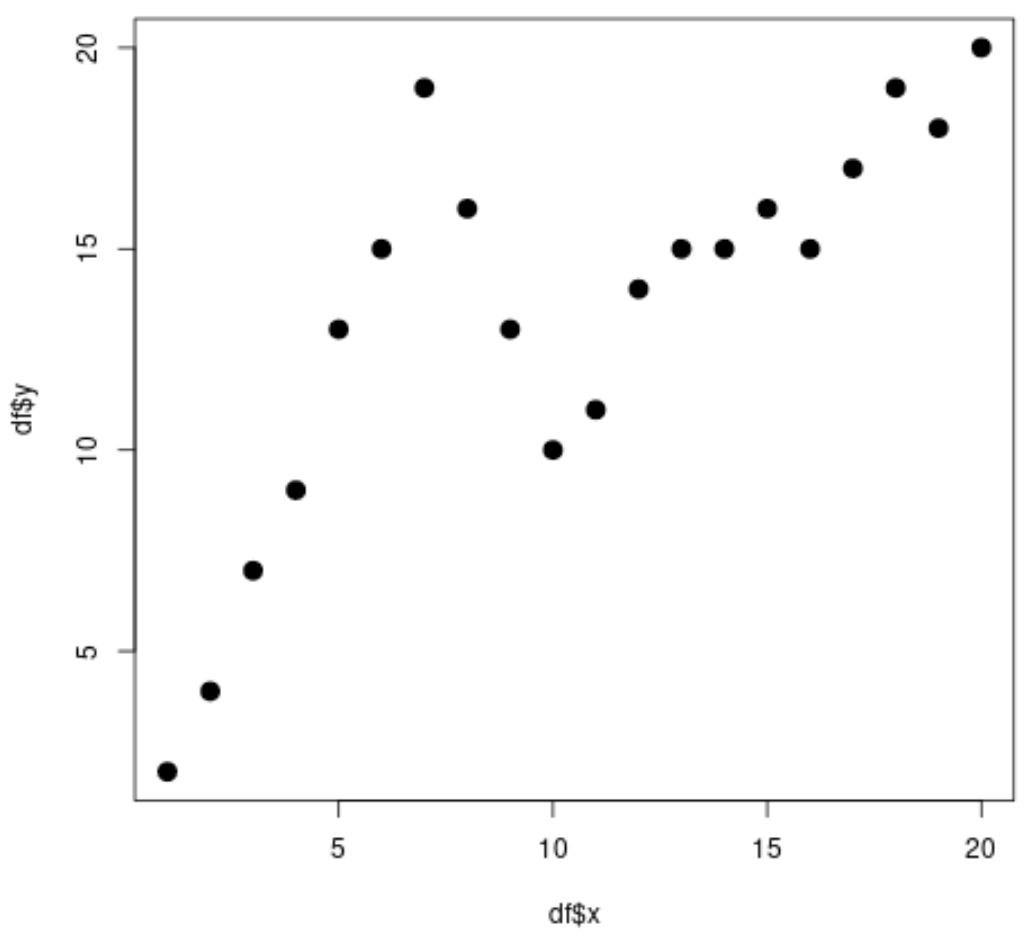
Offensichtlich ist die Beziehung zwischen x und y nicht linear und es scheint zwei Punkte oder „Knoten“ zu geben, an denen sich das Muster in den Daten bei x=7 und x=10 abrupt ändert.

Schritt 2: Passen Sie das einfache lineare Regressionsmodell an

Anschließend verwenden wir die Funktion lm() , um ein einfaches lineares Regressionsmodell an diesen Datensatz anzupassen und die Regressionslinie im Streudiagramm anzupassen:

 #fit simple linear regression model
linear_fit <- lm(df$y ~ df$x)

#view model summary
summary(linear_fit)

Call:
lm(formula = df$y ~ df$x)

Residuals:
    Min 1Q Median 3Q Max 
-5.2143 -1.6327 -0.3534 0.6117 7.8789 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 6.5632 1.4643 4.482 0.000288 ***
df$x 0.6511 0.1222 5.327 4.6e-05 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.152 on 18 degrees of freedom
Multiple R-squared: 0.6118, Adjusted R-squared: 0.5903 
F-statistic: 28.37 on 1 and 18 DF, p-value: 4.603e-05

#create scatterplot
plot(df$x, df$y, cex= 1.5 , pch= 19 )

#add regression line to scatterplot
abline(linear_fit) 

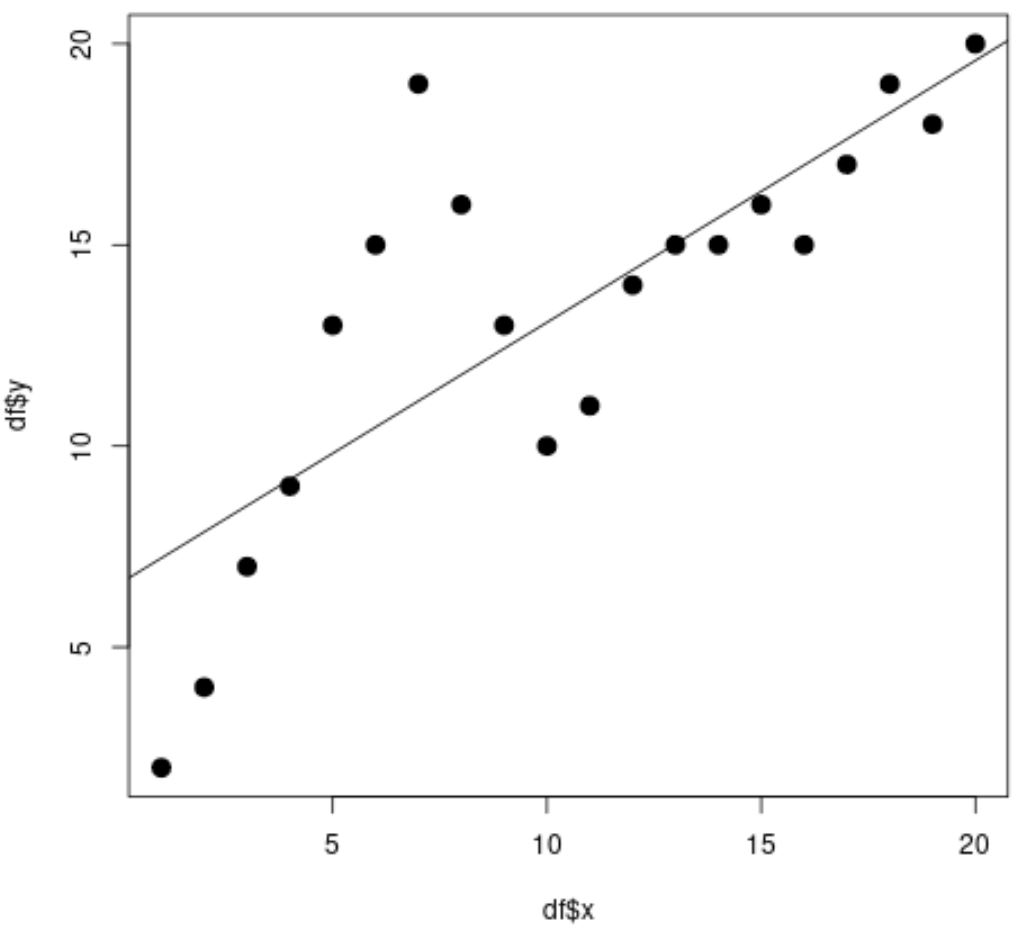
Aus dem Streudiagramm können wir erkennen, dass die einfache lineare Regressionslinie nicht gut zu den Daten passt.

Aus den Modellergebnissen können wir auch erkennen, dass der angepasste R-Quadrat-Wert 0,5903 beträgt.

Wir vergleichen dies mit dem angepassten R-Quadrat-Wert eines Spline-Modells.

Schritt 3: Passen Sie das Spline-Regressionsmodell an

Als Nächstes verwenden wir die Funktion bs() aus dem Splines- Paket, um ein Spline-Regressionsmodell mit zwei Knoten anzupassen, und zeichnen das angepasste Modell dann im Streudiagramm auf:

 library (splines)

#fit spline regression model
spline_fit <- lm(df$y ~ bs(df$x, knots=c( 7 , 10 )))

#view summary of spline regression model
summary(spline_fit)

Call:
lm(formula = df$y ~ bs(df$x, knots = c(7, 10)))

Residuals:
     Min 1Q Median 3Q Max 
-2.84883 -0.94928 0.08675 0.78069 2.61073 

Coefficients:
                            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 2.073 1.451 1.429 0.175    
bs(df$x, knots = c(7, 10))1 2.173 3.247 0.669 0.514    
bs(df$x, knots = c(7, 10))2 19.737 2.205 8.949 3.63e-07 ***
bs(df$x, knots = c(7, 10))3 3.256 2.861 1.138 0.274    
bs(df$x, knots = c(7, 10))4 19.157 2.690 7.121 5.16e-06 ***
bs(df$x, knots = c(7, 10))5 16.771 1.999 8.391 7.83e-07 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.568 on 14 degrees of freedom
Multiple R-squared: 0.9253, Adjusted R-squared: 0.8987 
F-statistic: 34.7 on 5 and 14 DF, p-value: 2.081e-07

#calculate predictions using spline regression model
x_lim <- range(df$x)
x_grid <- seq(x_lim[ 1 ], x_lim[ 2 ])
preds <- predict(spline_fit, newdata=list(x=x_grid))

#create scatter plot with spline regression predictions
plot(df$x, df$y, cex= 1.5 , pch= 19 )
lines(x_grid, preds) 

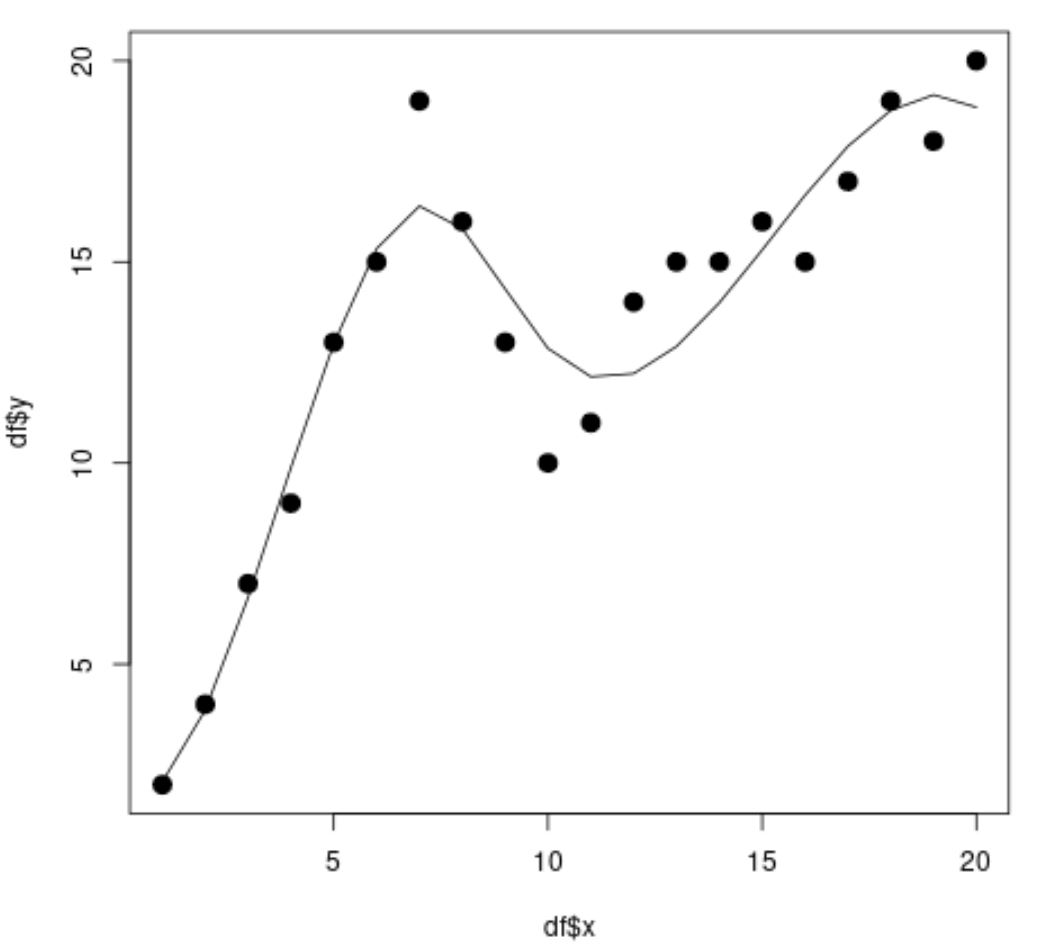
Aus dem Streudiagramm können wir ersehen, dass das Spline-Regressionsmodell die Daten recht gut anpassen kann.

Aus den Modellergebnissen können wir auch erkennen, dass der angepasste R-Quadrat-Wert 0,8987 beträgt.

Der angepasste R-Quadrat-Wert für dieses Modell ist viel höher als beim einfachen linearen Regressionsmodell, was uns zeigt, dass das Spline-Regressionsmodell die Daten besser anpassen kann.

Beachten Sie, dass wir für dieses Beispiel gewählt haben, dass sich die Knoten bei x=7 und x=10 befinden.

In der Praxis müssen Sie die Knotenstandorte selbst auswählen, je nachdem, wo sich Muster in den Daten zu ändern scheinen und basierend auf Ihrer Fachkenntnis.

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie Sie andere häufige Aufgaben in R ausführen:

So führen Sie eine multiple lineare Regression in R durch
So führen Sie eine exponentielle Regression in R durch
So führen Sie eine gewichtete Regression der kleinsten Quadrate in R durch