So erstellen und interpretieren sie eine roc-kurve in spss

Die logistische Regression ist eine statistische Methode, die wir verwenden, um ein Regressionsmodell anzupassen, wenn die Antwortvariable binär ist. Um zu bewerten, wie gut ein logistisches Regressionsmodell zu einem Datensatz passt, können wir uns die folgenden zwei Metriken ansehen:

• Sensitivität: Wahrscheinlichkeit, dass das Modell ein positives Ergebnis für eine Beobachtung vorhersagt, obwohl das Ergebnis tatsächlich positiv ist.
• Spezifität: Die Wahrscheinlichkeit, dass das Modell ein negatives Ergebnis für eine Beobachtung vorhersagt, obwohl das Ergebnis tatsächlich negativ ist.

Eine einfache Möglichkeit, diese beiden Metriken zu visualisieren, besteht darin, eine ROC-Kurve zu erstellen, bei der es sich um ein Diagramm handelt, das die Sensitivität und Spezifität eines logistischen Regressionsmodells anzeigt.

In diesem Tutorial wird erläutert, wie Sie in SPSS eine ROC-Kurve erstellen und interpretieren.

Beispiel: ROC-Kurve in SPSS

Nehmen wir an, wir haben den folgenden Datensatz, der zeigt, ob ein Basketballspieler in die NBA gedraftet wurde oder nicht (0 = nein, 1 = ja) sowie seinen Punktedurchschnitt pro Spiel im College:

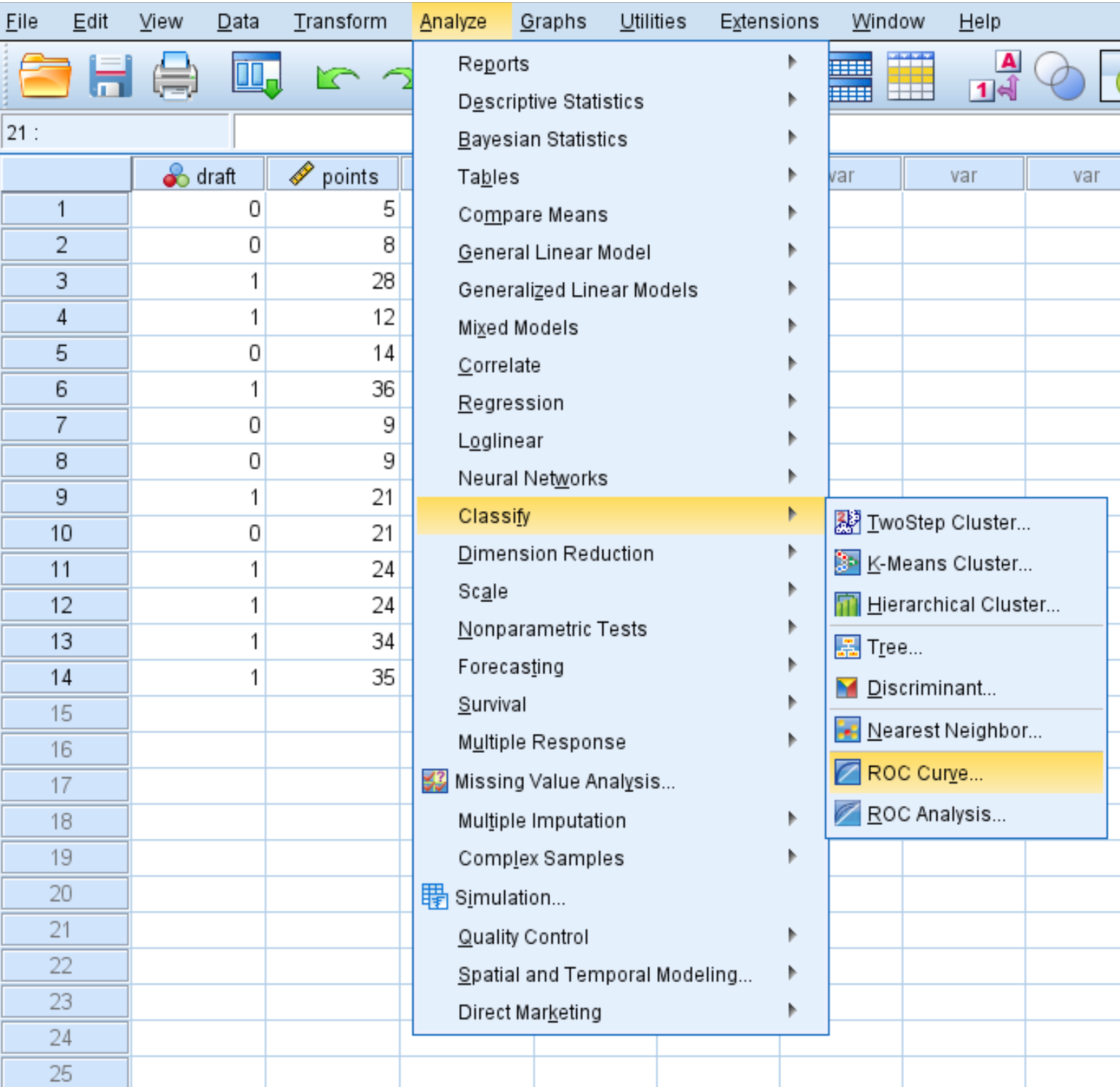
Um eine ROC-Kurve für diesen Datensatz zu erstellen, klicken Sie auf die Registerkarte „Analysieren “, dann auf „Klassifizieren “ und dann auf „ROC-Kurve“ :

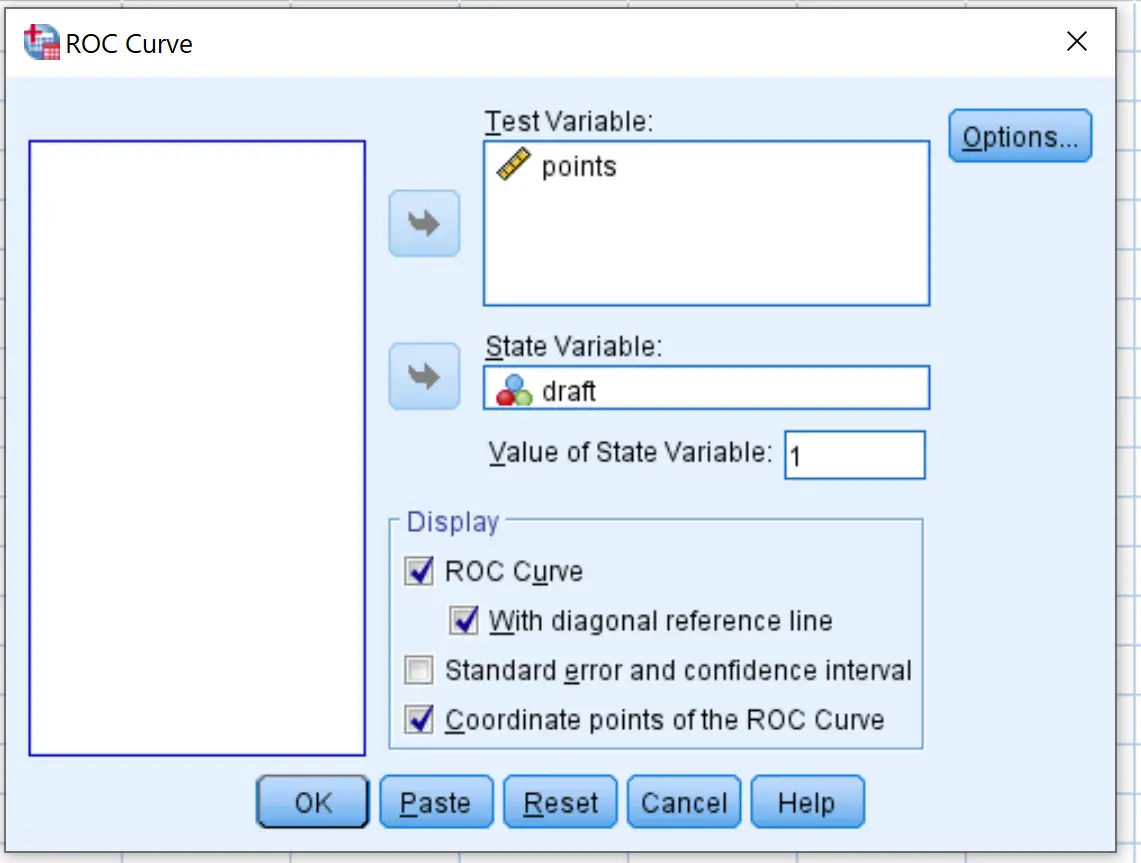
Ziehen Sie im neuen Fenster, das erscheint, die Entwurfsvariable in den Bereich mit der Bezeichnung „Statusvariable“. Setzen Sie den Wert der Statusvariablen auf 1 . (Dies ist der Wert, der angibt, dass ein Spieler gedraftet wurde). Ziehen Sie die Variablenpunkte in den Bereich mit der Bezeichnung „Testvariable“.

Aktivieren Sie die Kontrollkästchen neben Mit diagonaler Referenzlinie und ROC-Kurvenpunktkoordinaten . Klicken Sie dann auf OK .

So interpretieren Sie das Ergebnis:

Zusammenfassung der Dateiverarbeitung:

In dieser Tabelle wird die Gesamtzahl der positiven und negativen Fälle im Datensatz angezeigt. In diesem Beispiel wurden 8 Spieler gedraftet (positives Ergebnis) und 6 Spieler wurden nicht gedraftet (negatives Ergebnis):

ROC-Kurve:

Die Receiver Operating Characteristic (ROC)-Kurve ist ein Diagramm der Sensitivitätswerte gegenüber der Spezifität 1, wenn sich der Schwellenwert von 0 auf 1 ändert:

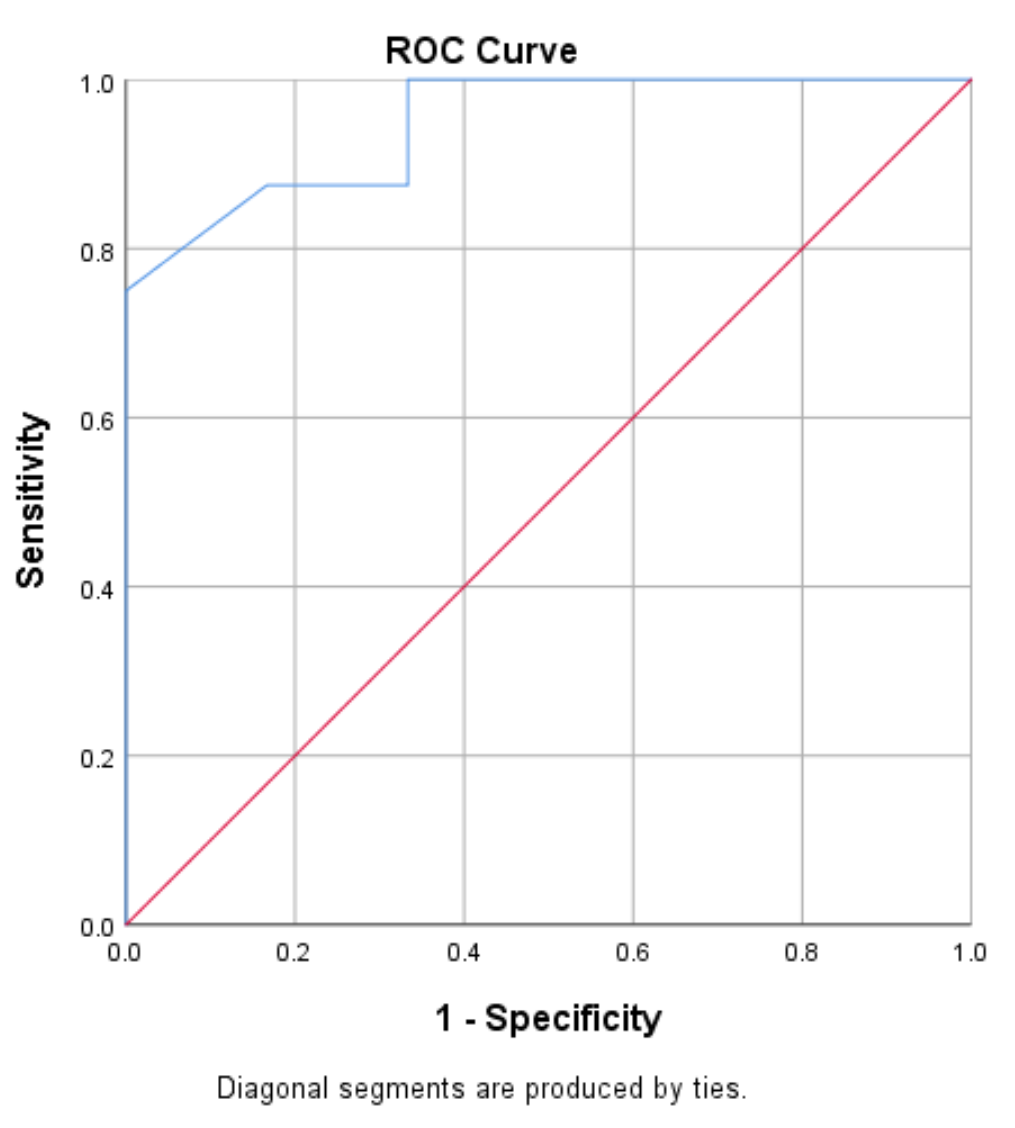
Ein Modell mit hoher Sensitivität und Spezifität weist eine ROC-Kurve auf, die in die obere linke Ecke des Diagramms passt. Ein Modell mit geringer Sensitivität und geringer Spezifität weist eine Kurve nahe der 45-Grad-Diagonale auf.

Wir können sehen, dass die ROC-Kurve (die blaue Linie) in diesem Beispiel die obere linke Ecke des Diagramms umschließt, was darauf hindeutet, dass das Modell anhand ihrer durchschnittlichen Punkte pro Spiel gut vorhersagen kann, ob Spieler gedraftet werden oder nicht . .

Fläche unter der Kurve:

Die Fläche unter der Kurve gibt uns eine Vorstellung von der Fähigkeit des Modells, zwischen positiven und negativen Ergebnissen zu unterscheiden. Die AUC kann zwischen 0 und 1 liegen. Je höher die AUC, desto besser kann das Modell die Ergebnisse korrekt klassifizieren.

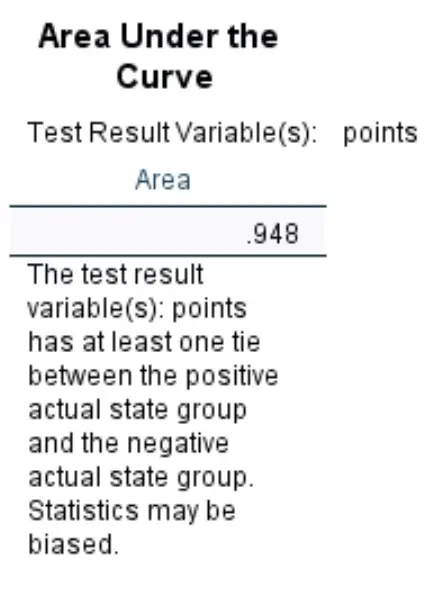
Wir können sehen, dass die AUC für dieses spezielle logistische Regressionsmodell 0,948 beträgt, was extrem hoch ist. Dies weist darauf hin, dass das Modell gut vorhersagen kann, ob ein Spieler gedraftet wird oder nicht.

Koordinaten der Kurve:

Diese letzte Tabelle zeigt die Sensitivität und Spezifität 1 der ROC-Kurve für verschiedene Schwellenwerte.

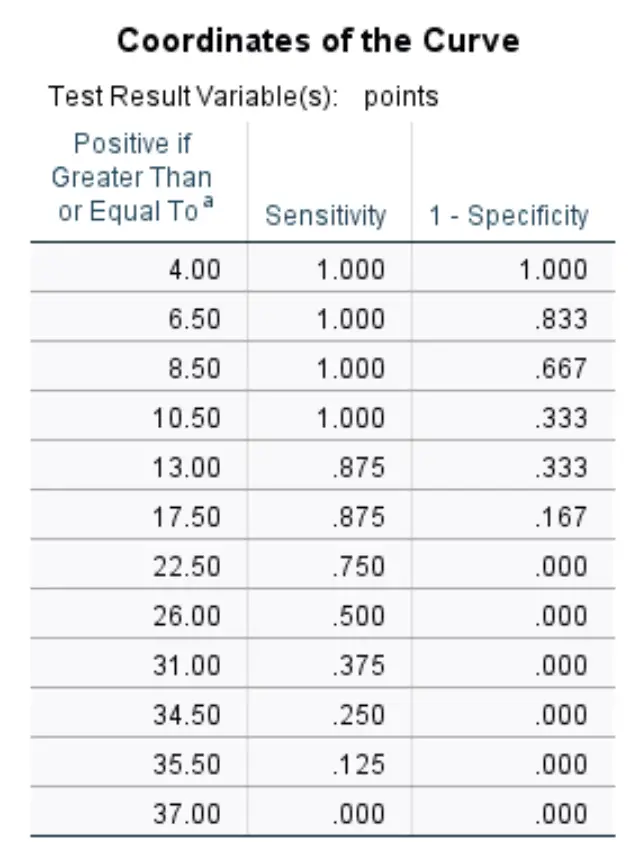
Zum Beispiel:

Wenn wir einen Schwellenwert von 8,50 zulassen, bedeutet dies, dass wir davon ausgehen, dass jeder Spieler, der weniger als 8,50 Punkte pro Spiel erzielt, nicht gedraftet wird, und dass jeder Spieler, der mehr als 8,50 Punkte pro Spiel erzielt, gedraftet wird.

Wenn wir dies als Schwellenwert verwenden, wäre unsere Sensitivität 100 % (da jeder Spieler, der weniger als 8,50 Punkte pro Spiel erzielte, tatsächlich nicht gedraftet wurde) und unsere Spezifität 1 wäre 66,7 % (da 8 von 12 Spielern mehr als 8,50 Punkte erzielten). pro Spiel wurden gedraftet).

In der obigen Tabelle können wir die Sensitivität und Spezifität 1 für jeden potenziellen Schwellenwert sehen.