So führen sie eine multiple lineare regression in spss durch
Die multiple lineare Regression ist eine Methode, mit der wir die Beziehung zwischen zwei oder mehr erklärenden Variablen und einer Antwortvariablen verstehen können.
In diesem Tutorial wird erläutert, wie Sie in SPSS eine multiple lineare Regression durchführen.
Beispiel: Multiple lineare Regression in SPSS
Angenommen, wir möchten wissen, ob die Anzahl der Lernstunden und die Anzahl der abgelegten Übungsprüfungen einen Einfluss auf die Note haben, die ein Student bei einer bestimmten Prüfung erhält. Um dies zu untersuchen, können wir eine multiple lineare Regression unter Verwendung der folgenden Variablen durchführen:
Erklärende Variablen:
- Stunden studiert
- Vorbereitungsprüfungen bestanden
Antwortvariable:
- Prüfungsergebnis
Führen Sie die folgenden Schritte aus, um diese multiple lineare Regression in SPSS durchzuführen.
Schritt 1: Geben Sie die Daten ein.
Geben Sie für 20 Studierende folgende Daten zur Anzahl der Lernstunden, abgelegten Vorbereitungsprüfungen und erhaltenen Prüfungsergebnisse ein:
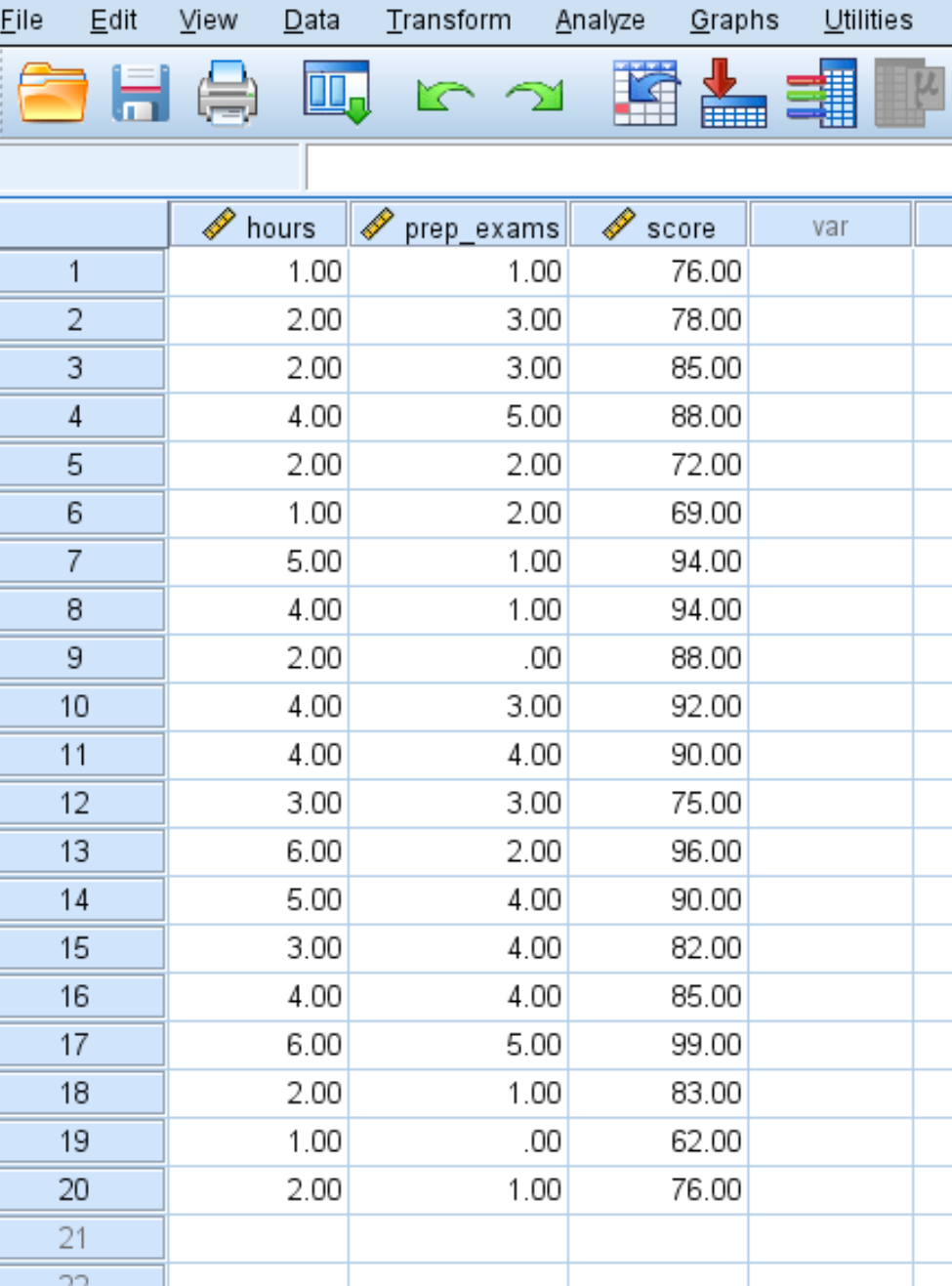
Schritt 2: Führen Sie eine multiple lineare Regression durch.
Klicken Sie auf die Registerkarte „Analysieren“ , dann auf „Regression“ und dann auf „Linear“ :
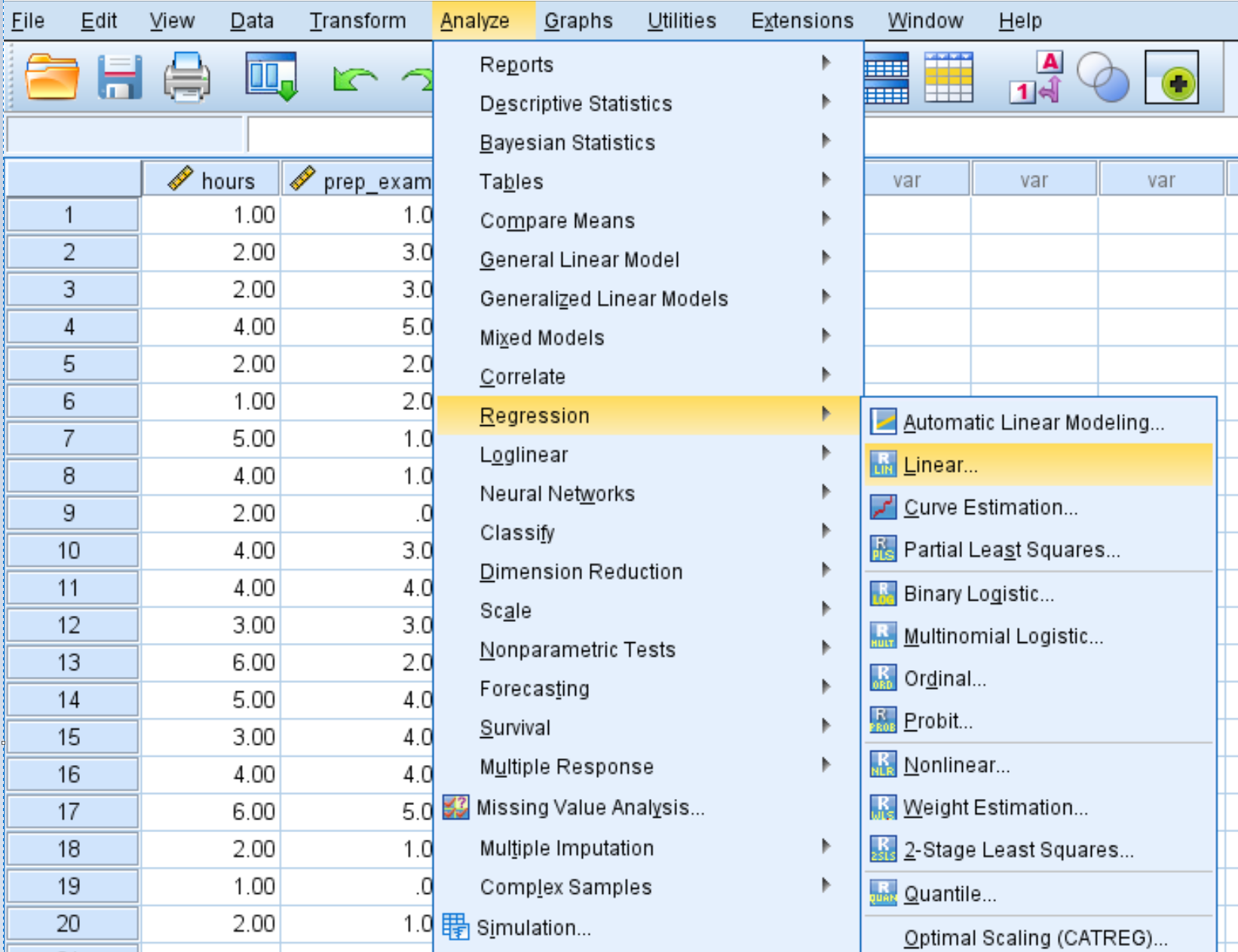
Ziehen Sie die Variable „ score“ in das Feld „Abhängig“. Ziehen Sie die Variablen „hours“ und „prep_exams“ in das Feld „Independent(s)“. Klicken Sie dann auf OK .
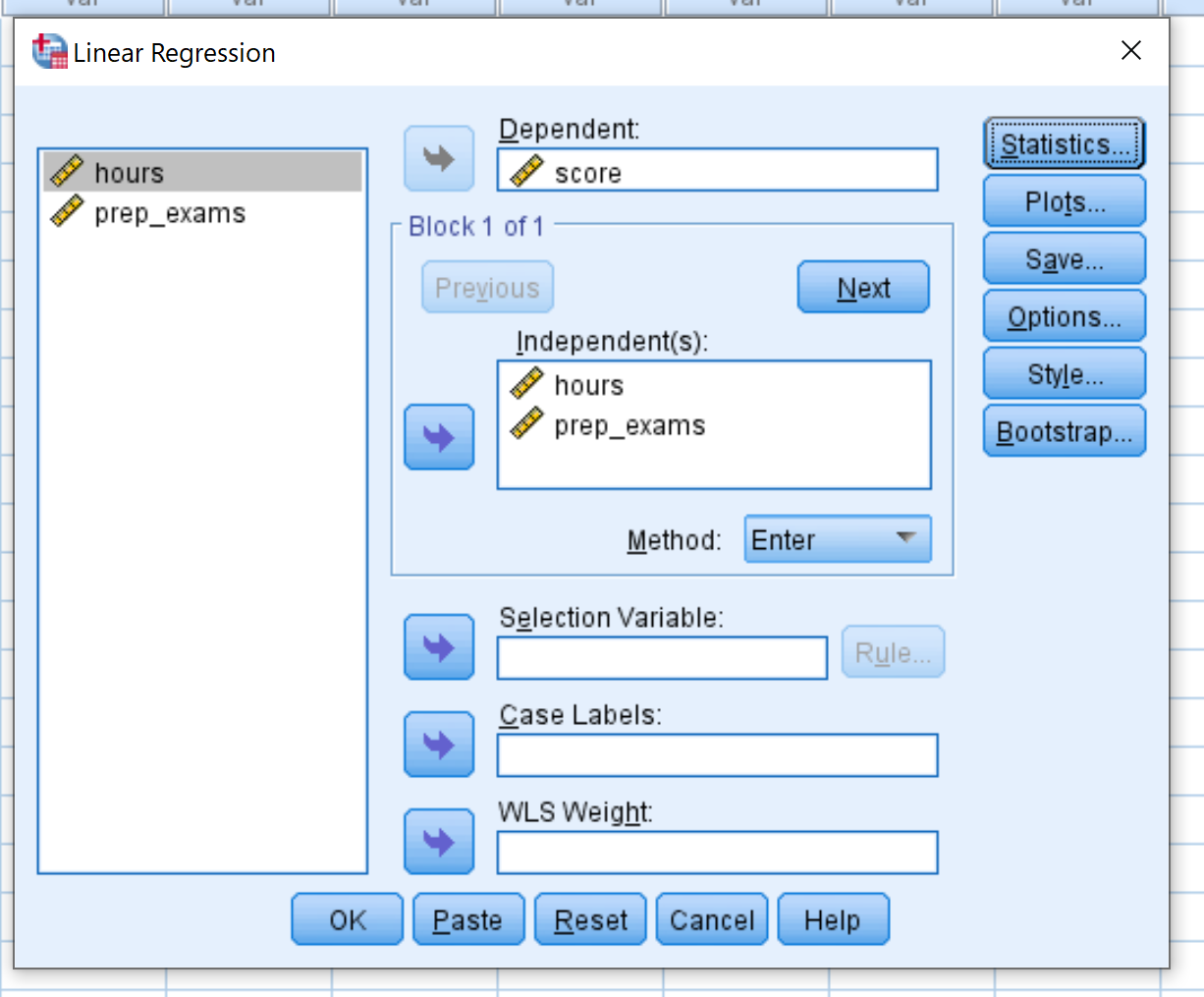
Schritt 3: Interpretieren Sie das Ergebnis.
Sobald Sie auf „OK“ klicken, werden die Ergebnisse der multiplen linearen Regression in einem neuen Fenster angezeigt.
Die erste Tabelle, die uns interessiert, heißt Model Summary :
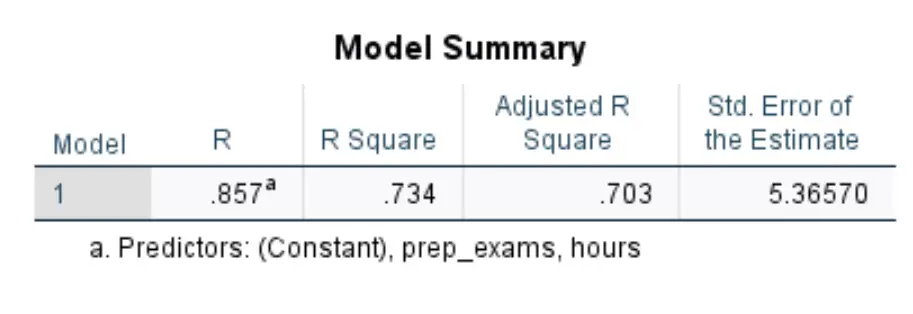
So interpretieren Sie die relevantesten Zahlen in dieser Tabelle:
- R-Quadrat: Dies ist der Anteil der Varianz in der Antwortvariablen, der durch die erklärenden Variablen erklärt werden kann. In diesem Beispiel lassen sich 73,4 % der Abweichungen bei den Prüfungsergebnissen durch die Lernstunden und die Anzahl der abgelegten Vorbereitungsprüfungen erklären.
- Standard. Schätzfehler: Der Standardfehler ist der durchschnittliche Abstand zwischen den beobachteten Werten und der Regressionsgeraden. In diesem Beispiel weichen die beobachteten Werte im Durchschnitt um 5,3657 Einheiten von der Regressionsgeraden ab.
Die nächste Tabelle, die uns interessiert, heißt ANOVA :
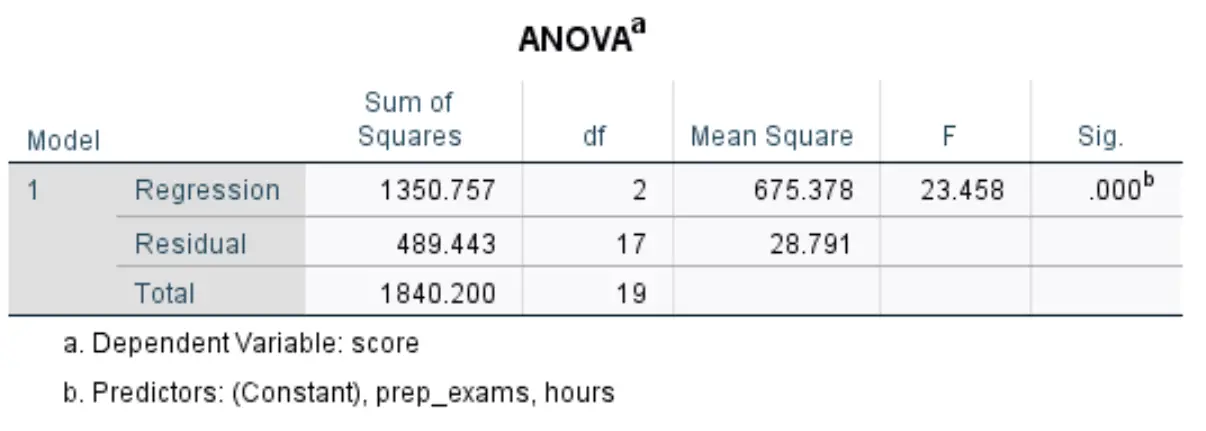
So interpretieren Sie die relevantesten Zahlen in dieser Tabelle:
- F: Dies ist die Gesamt-F-Statistik für das Regressionsmodell, berechnet als mittlere quadratische Regression/mittleres quadratisches Residuum.
- Sig: Dies ist der p-Wert, der der gesamten F-Statistik zugeordnet ist. Dies sagt uns, ob das Regressionsmodell als Ganzes statistisch signifikant ist oder nicht. Mit anderen Worten sagt es uns, ob die beiden erklärenden Variablen zusammen einen statistisch signifikanten Zusammenhang mit der Antwortvariablen haben. In diesem Fall beträgt der p-Wert 0,000, was darauf hinweist, dass die erklärenden Variablen, gelernte Stunden und absolvierte Vorbereitungsprüfungen, einen statistisch signifikanten Zusammenhang mit dem Prüfungsergebnis haben.
Die folgende Tabelle, die uns interessiert, trägt den Titel Koeffizienten :
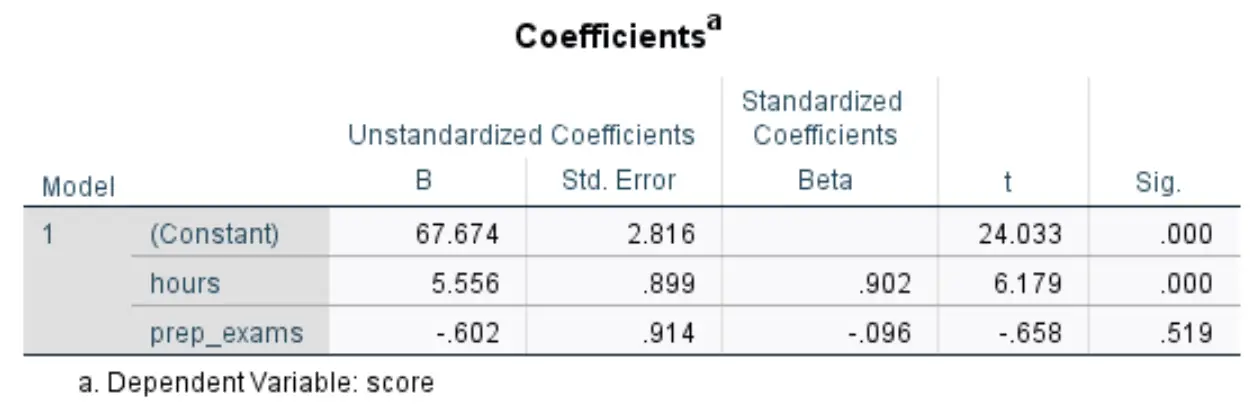
So interpretieren Sie die relevantesten Zahlen in dieser Tabelle:
- B unstandardisiert (konstant): Dies gibt uns den Durchschnittswert der Antwortvariablen an, wenn beide Prädiktorvariablen Null sind. In diesem Beispiel beträgt die durchschnittliche Prüfungspunktzahl 67.674 , wenn die Lernstunden und die absolvierten Vorbereitungsprüfungen beide Null sind.
- Nicht standardisiertes B (Stunden): Dies zeigt uns die durchschnittliche Änderung der Prüfungsergebnisse, die mit einer Erhöhung der Lernstunden um eine Einheit verbunden ist, unter der Annahme, dass die Anzahl der abgelegten Vorbereitungsprüfungen konstant bleibt. In diesem Fall ist jede zusätzliche Lernstunde mit einer Steigerung der Prüfungspunktzahl um 5.556 Punkte verbunden, vorausgesetzt, die Anzahl der abgelegten Übungsprüfungen bleibt konstant.
- Nicht standardisiertes B (prep_exams): Dies zeigt uns die durchschnittliche Änderung der Prüfungspunktzahl, die mit einem Anstieg der abgelegten Vorbereitungsprüfungen um eine Einheit einhergeht, unter der Annahme, dass die Anzahl der gelernten Stunden konstant bleibt. In diesem Fall ist jede zusätzlich abgelegte Vorbereitungsprüfung mit einer Verschlechterung der Prüfungspunktzahl um 0,602 Punkte verbunden, vorausgesetzt, die Anzahl der Lernstunden bleibt konstant.
- Sig. (Stunden): Dies ist der p-Wert für die erklärende Variable Stunden . Da dieser Wert (0,000) kleiner als 0,05 ist, können wir daraus schließen, dass die gelernten Stunden einen statistisch signifikanten Zusammenhang mit den Prüfungsergebnissen haben.
- Sig. (prep_exams): Dies ist der p-Wert für die erklärende Variable prep_exams . Da dieser Wert (0,519) nicht kleiner als 0,05 ist, können wir nicht schließen, dass die Anzahl der abgelegten Vorbereitungsprüfungen einen statistisch signifikanten Zusammenhang mit dem Prüfungsergebnis hat.
Schließlich können wir eine Regressionsgleichung erstellen, indem wir die in der Tabelle gezeigten Werte für „ constant “, „hours “ und „prep_exams “ verwenden. In diesem Fall wäre die Gleichung:
Geschätzte Prüfungspunktzahl = 67,674 + 5,556*(Stunden) – 0,602*(prep_exams)
Mit dieser Gleichung können wir die geschätzte Prüfungspunktzahl eines Studenten ermitteln, basierend auf der Anzahl der Lernstunden und der Anzahl der abgelegten Übungsprüfungen. Beispielsweise sollte ein Student, der 3 Stunden lernt und 2 Vorbereitungsprüfungen ablegt, eine Prüfungspunktzahl von 83,1 erhalten:
Geschätztes Prüfungsergebnis = 67,674 + 5,556*(3) – 0,602*(2) = 83,1
Hinweis: Da festgestellt wurde, dass die erklärende Variable für Vorbereitungsprüfungen statistisch nicht signifikant ist, können wir sie aus dem Modell entfernen und stattdessen eine einfache lineare Regression durchführen, bei der die untersuchten Stunden die einzige erklärende Variable sind.