So führen sie eine quadratische regression in spss durch
Wenn zwei Variablen in einer linearen Beziehung stehen, können Sie häufig eine einfache lineare Regression verwenden , um ihre Beziehung zu quantifizieren.
Eine einfache lineare Regression funktioniert jedoch nicht gut, wenn zwei Variablen in einer nichtlinearen Beziehung zueinander stehen. In diesen Fällen können Sie es mit der quadratischen Regression versuchen.
In diesem Tutorial wird erläutert, wie Sie eine quadratische Regression in SPSS durchführen.
Beispiel: Quadratische Regression in SPSS
Angenommen, wir möchten den Zusammenhang zwischen der Anzahl der geleisteten Arbeitsstunden und dem Glück verstehen. Wir haben die folgenden Daten zur Anzahl der pro Woche geleisteten Arbeitsstunden und zum gemeldeten Grad der Zufriedenheit (auf einer Skala von 0 bis 100) für 16 verschiedene Personen:
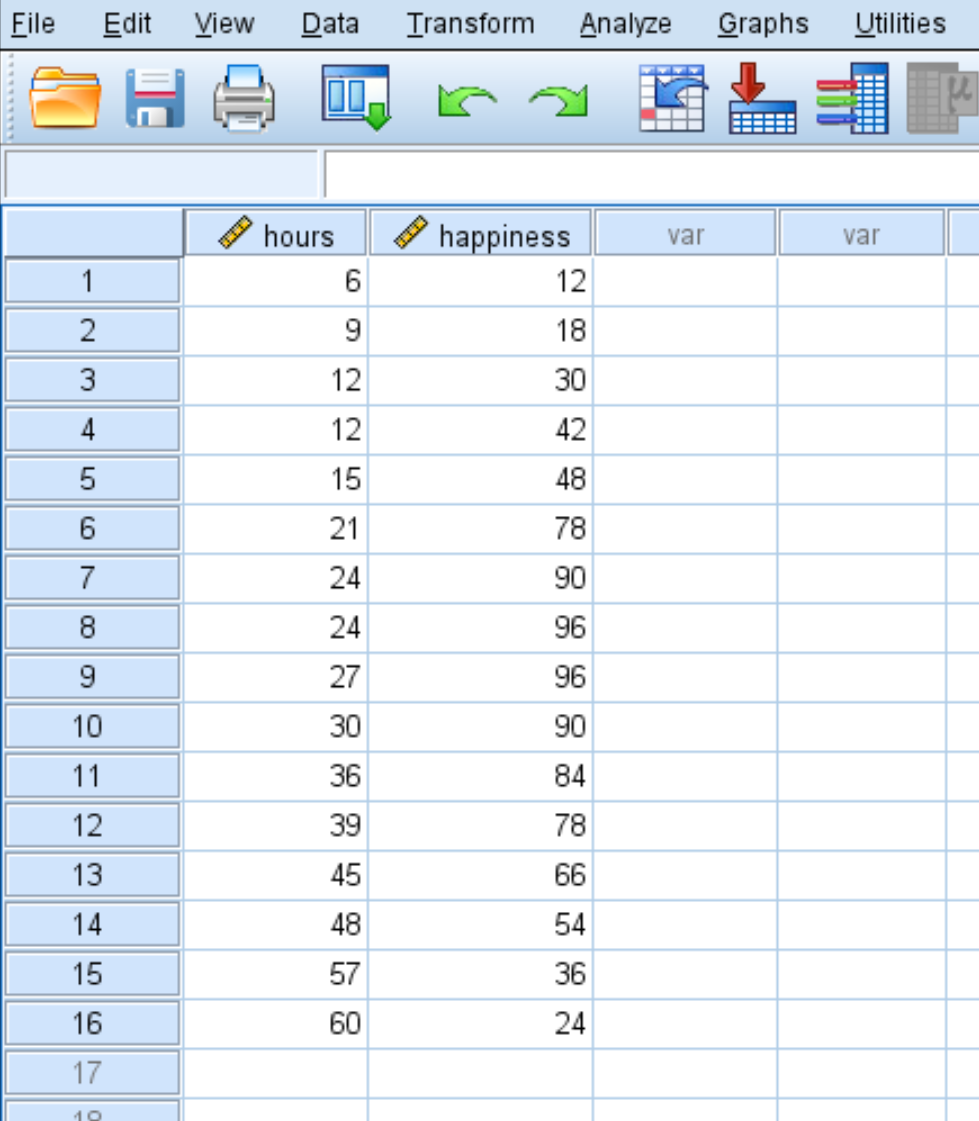
Führen Sie die folgenden Schritte aus, um eine quadratische Regression in SPSS durchzuführen.
Schritt 1: Visualisieren Sie die Daten.
Bevor wir eine quadratische Regression durchführen, erstellen wir ein Streudiagramm, um die Beziehung zwischen geleisteten Arbeitsstunden und Glück zu visualisieren und zu überprüfen, ob zwischen den beiden Variablen tatsächlich eine quadratische Beziehung besteht.
Klicken Sie auf die Registerkarte „Diagramme“ und dann auf „Diagrammersteller“ :
Wählen Sie im neuen Fenster, das angezeigt wird, „Streuung/Punkt“ aus der Liste „Auswählen “ aus. Ziehen Sie dann das Diagramm mit der Bezeichnung „Simple Scatter“ in das Hauptbearbeitungsfenster. Ziehen Sie variable Stunden auf der X-Achse und Glück auf der Y-Achse. Klicken Sie dann auf OK .
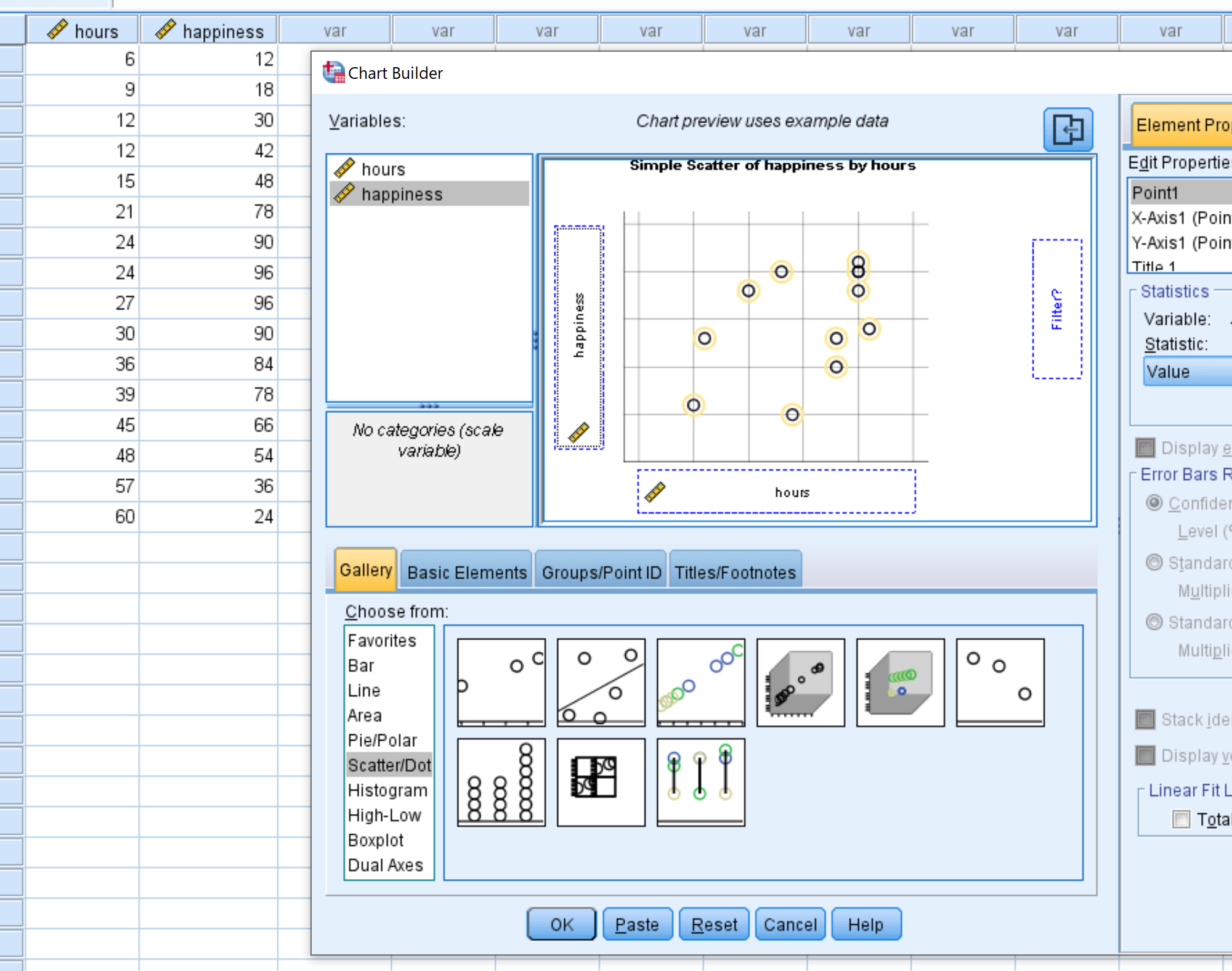
Das folgende Streudiagramm wird angezeigt:
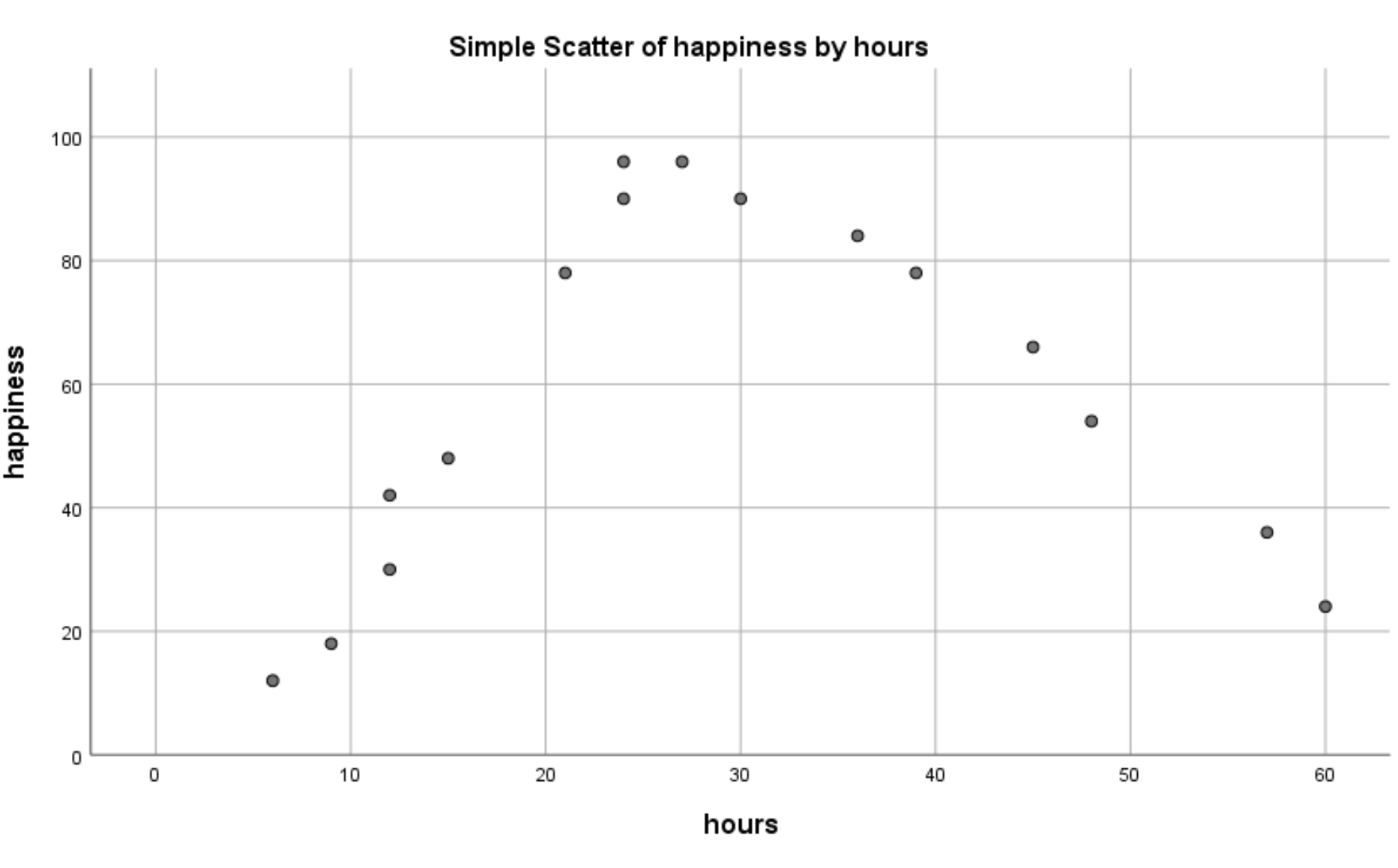
Wir können deutlich erkennen, dass es einen nichtlinearen Zusammenhang zwischen geleisteten Arbeitsstunden und Glück gibt. Dies zeigt uns, dass die quadratische Regression in dieser Situation eine geeignete Technik ist.
Schritt 2: Erstellen Sie eine neue Variable.
Bevor wir eine quadratische Regression durchführen können, müssen wir eine Prädiktorvariable für Stunden 2 erstellen.
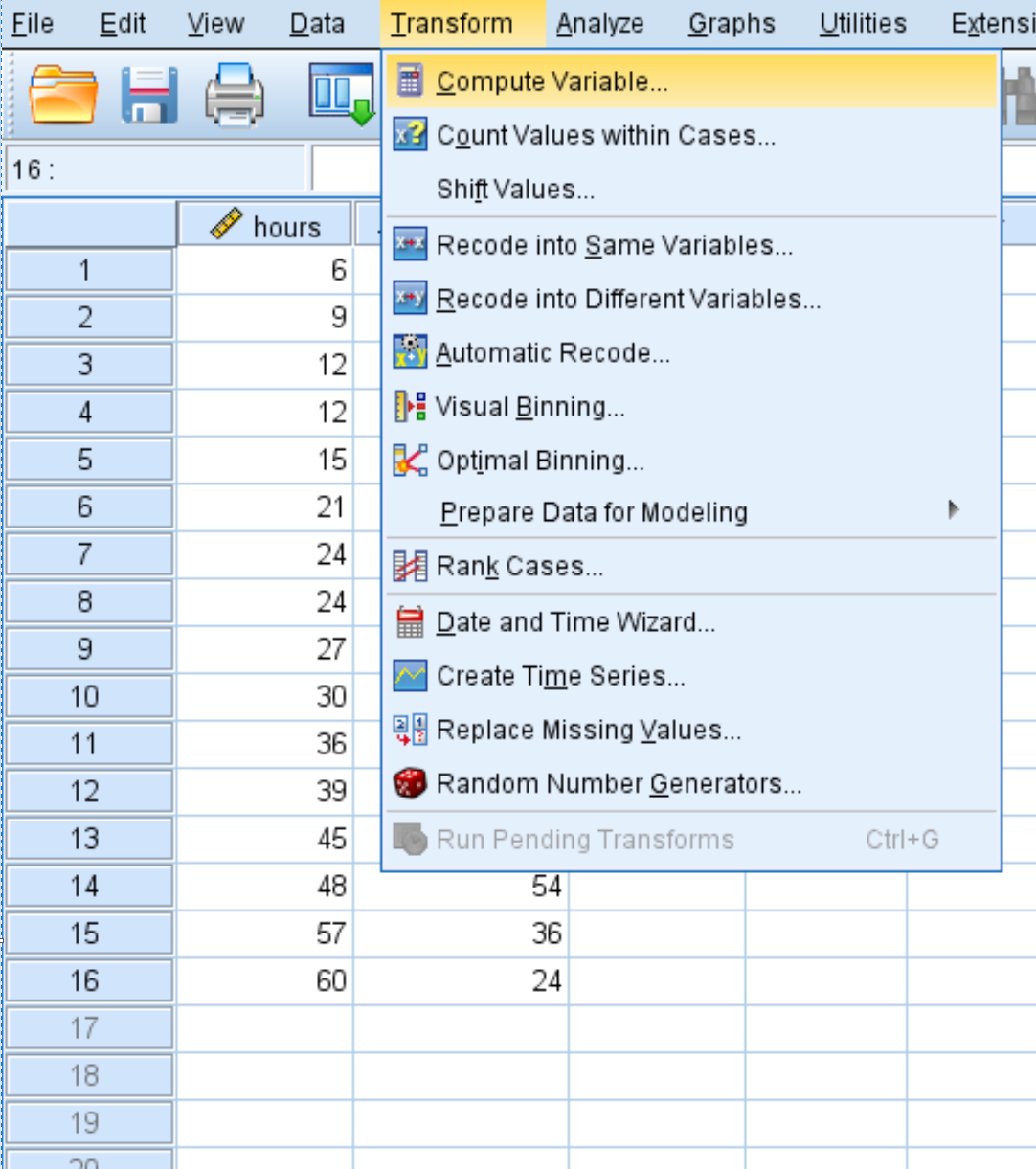
Klicken Sie auf die Registerkarte „Transformation“ und dann auf „Variable berechnen“ :
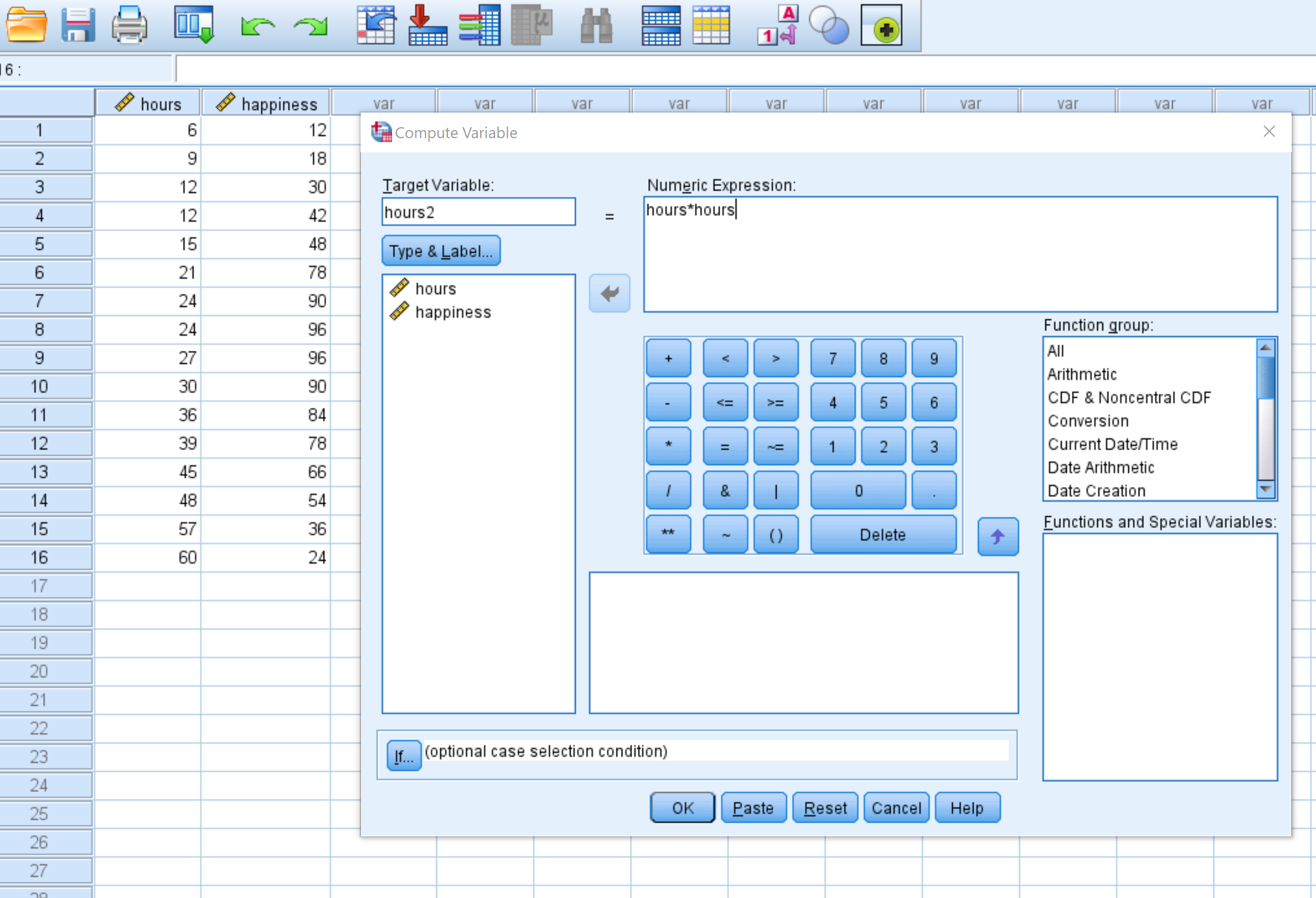
Benennen Sie im neuen Fenster, das erscheint, die Zielvariable „hours2“ und setzen Sie sie auf „hours*hours“ :
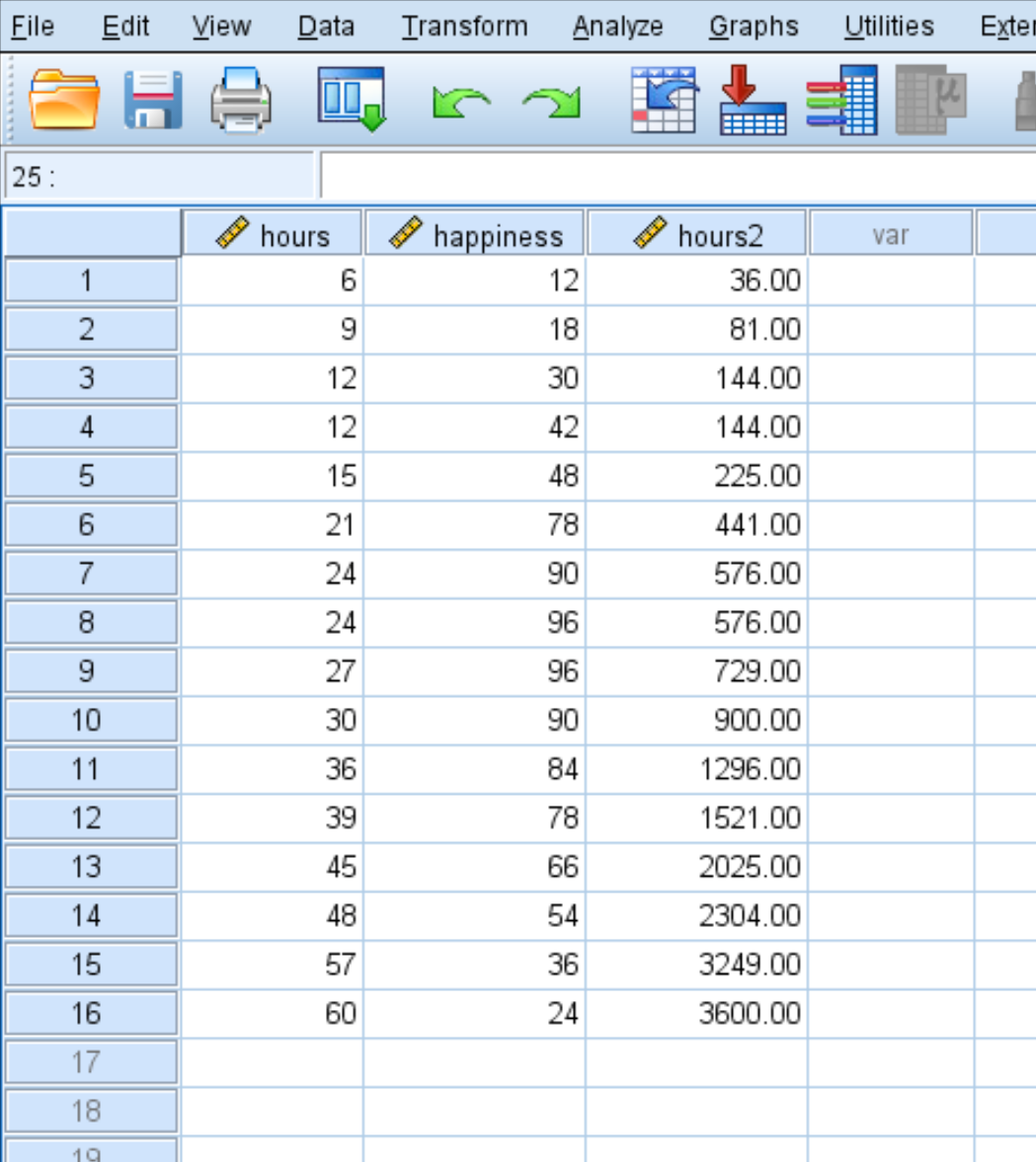
Sobald Sie auf „OK“ klicken, wird die Variable „hours2“ in einer neuen Spalte angezeigt:
Schritt 3: Führen Sie eine quadratische Regression durch.
Als nächstes führen wir eine quadratische Regression durch. Klicken Sie auf die Registerkarte „Analysieren“ , dann auf „Regression“ und dann auf „Linear“ :
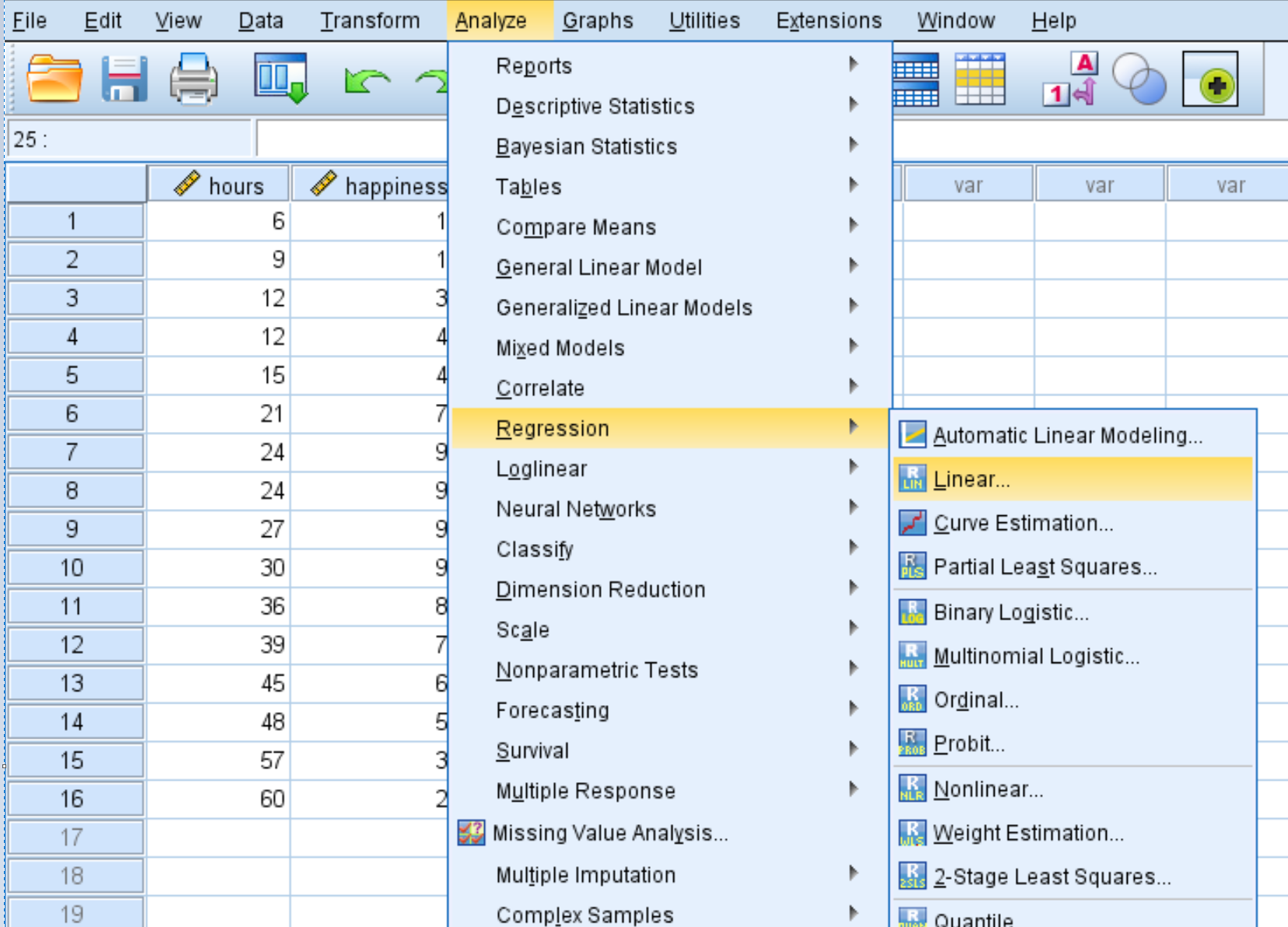
Ziehen Sie im neuen Fenster, das erscheint, das Glück in das Feld mit der Bezeichnung „Abhängig“. Ziehen Sie Hours und Hours2 in das Feld mit der Bezeichnung Independent(s). Klicken Sie dann auf OK .
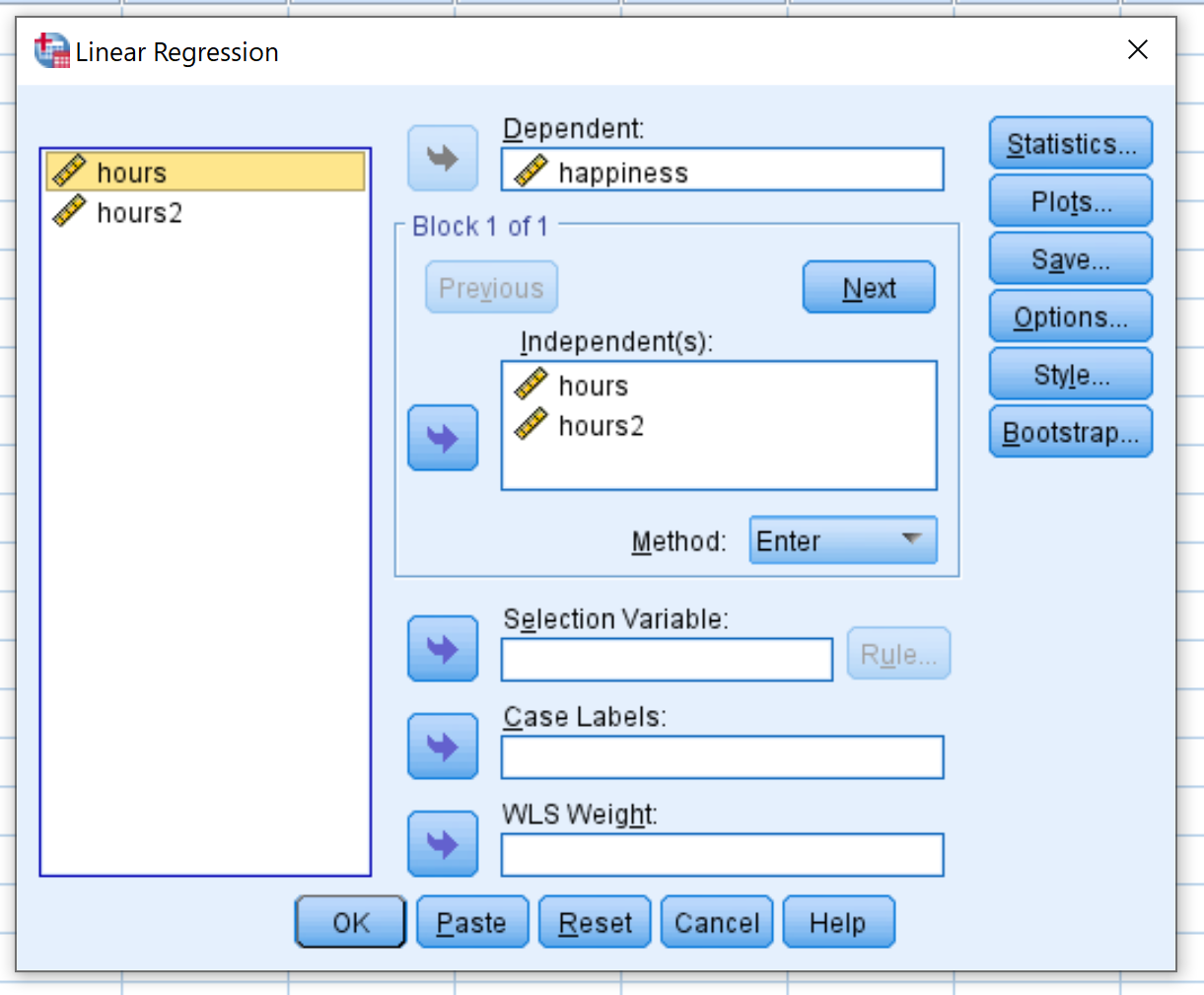
Schritt 4: Interpretieren Sie die Ergebnisse.
Sobald Sie auf OK klicken, werden die Ergebnisse der quadratischen Regression in einem neuen Fenster angezeigt.
Die erste Tabelle, die uns interessiert, heißt Model Summary :

So interpretieren Sie die relevantesten Zahlen in dieser Tabelle:
- R-Quadrat: Dies ist der Anteil der Varianz in der Antwortvariablen, der durch die erklärenden Variablen erklärt werden kann. In diesem Beispiel können 90,9 % der Glücksschwankungen durch die Variablen „ Stunden “ und „Stunden 2“ erklärt werden.
- Standard. Schätzfehler: Der Standardfehler ist der durchschnittliche Abstand zwischen den beobachteten Werten und der Regressionsgeraden. In diesem Beispiel weichen die beobachteten Werte im Durchschnitt um 9.519 Einheiten von der Regressionsgeraden ab.
Die nächste Tabelle, die uns interessiert, heißt ANOVA :
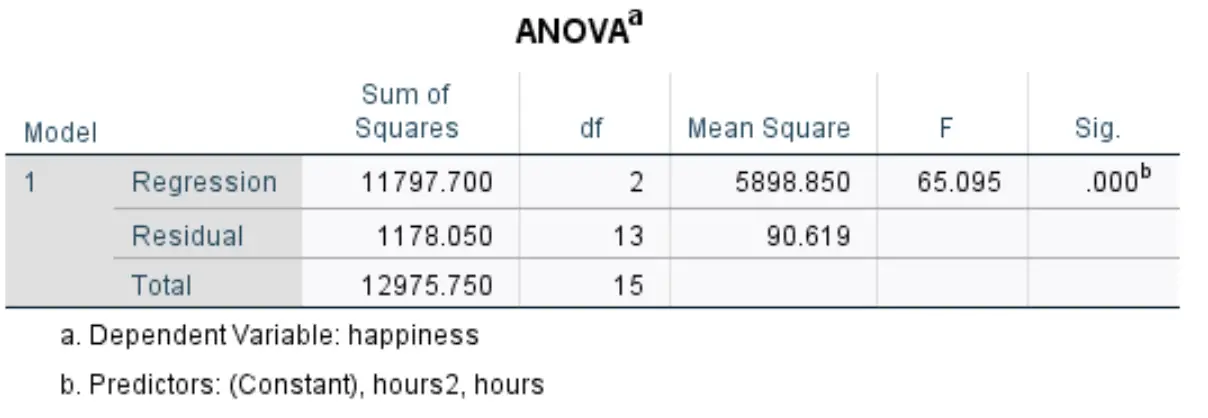
So interpretieren Sie die relevantesten Zahlen in dieser Tabelle:
- F: Dies ist die Gesamt-F-Statistik für das Regressionsmodell, berechnet als mittlere quadratische Regression/mittleres quadratisches Residuum.
- Sig: Dies ist der p-Wert, der der gesamten F-Statistik zugeordnet ist. Dies sagt uns, ob das Regressionsmodell als Ganzes statistisch signifikant ist oder nicht. In diesem Fall beträgt der p-Wert 0,000, was darauf hinweist, dass die erklärenden Variablen Stunden und Stunden 2 zusammen einen statistisch signifikanten Zusammenhang mit dem Prüfungsergebnis haben.
Die folgende Tabelle, die uns interessiert, trägt den Titel Koeffizienten :
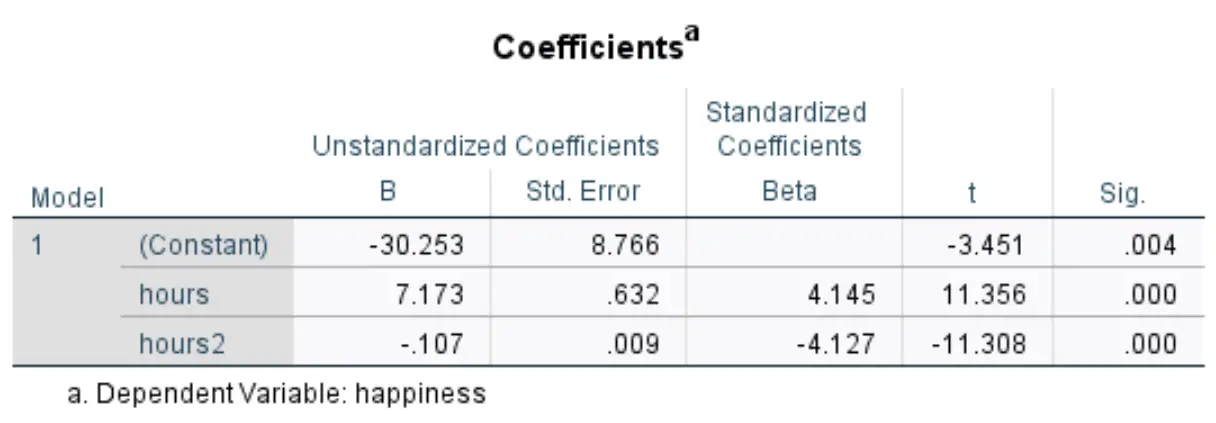
Wir können die Werte in der Spalte „Unstandardisiert B“ verwenden, um die geschätzte Regressionsgleichung für diesen Datensatz zu bilden:
Geschätzter Glücksgrad = -30,253 + 7,173*(Stunden) – 0,107*(Stunden 2 )
Mit dieser Gleichung können wir das geschätzte Glücksniveau einer Person basierend auf der Anzahl der pro Woche geleisteten Arbeitsstunden ermitteln. Beispielsweise sollte eine Person, die 60 Stunden pro Woche arbeitet, einen Glücksgrad von 14,97 haben:
Geschätzter Glücksgrad = -30,253 + 7,173*(60) – 0,107*(60 2 ) = 14,97 .
Umgekehrt sollte eine Person, die 30 Stunden pro Woche arbeitet, einen Glücksgrad von 88,65 haben:
Geschätzter Glücksgrad = -30,253 + 7,173*(30) – 0,107*(30 2 ) = 88,65 .
Schritt 5: Melden Sie die Ergebnisse.
Abschließend möchten wir die Ergebnisse unserer quadratischen Regression berichten. Hier ist ein Beispiel dafür:
Eine quadratische Regression wurde durchgeführt, um die Beziehung zwischen der Anzahl der Arbeitsstunden einer Person und ihrem entsprechenden Zufriedenheitsgrad (gemessen von 0 bis 100) zu quantifizieren. Für die Analyse wurde eine Stichprobe von 16 Personen herangezogen.
Die Ergebnisse zeigten, dass zwischen den erklärenden Variablen Stunden und Stunden 2 und der Antwortvariablen Glück ein statistisch signifikanter Zusammenhang bestand (F(2, 13) = 65,095, p < 0,000).
Zusammen machten diese beiden erklärenden Variablen 90,9 % der Glücksvariabilität aus.
Es stellte sich heraus, dass die Regressionsgleichung lautete:
Geschätzter Glücksgrad = -30,253 + 7,173 (Stunden) – 0,107 ( 2 Stunden)