Ein sanfter leitfaden zur quadratsumme: sst, ssr, sse
Die lineare Regression wird verwendet, um eine Linie zu finden, die am besten zu einem Datensatz passt.
Wir verwenden oft drei verschiedene Quadratsummenwerte, um zu messen, wie gut die Regressionslinie tatsächlich zu den Daten passt:
1. Summe der Gesamtquadrate (SST) – Die Summe der Quadrate der Differenzen zwischen einzelnen Datenpunkten (y i ) und dem Mittelwert der Antwortvariablen ( y ).
- SST = Σ(y i – y ) 2
2. Summe der Quadrate-Regression (SSR) – Die Summe der Quadrate der Differenzen zwischen den vorhergesagten Datenpunkten (ŷ i ) und dem Mittelwert der Antwortvariablen ( y ).
- SSR = Σ(ŷ i – y ) 2
3. Fehlerquadratsumme (SSE) – Die Summe der Quadrate der Differenzen zwischen den vorhergesagten Datenpunkten (ŷ i ) und den beobachteten Datenpunkten (y i ).
- SSE = Σ(ŷ i – y i ) 2
Zwischen diesen drei Maßen besteht folgender Zusammenhang:
SST = SSR + SSE
Wenn wir also zwei dieser Messungen kennen, können wir die dritte mithilfe einfacher Algebra berechnen.
SSR, SST und R-Quadrat
Das R-Quadrat , manchmal auch Bestimmtheitsmaß genannt, ist ein Maß dafür, wie gut ein lineares Regressionsmodell zu einem Datensatz passt. Sie stellt den Anteil der Varianz in der Antwortvariablen dar, der durch die Prädiktorvariable erklärt werden kann.
Der R-Quadrat-Wert kann zwischen 0 und 1 liegen. Ein Wert von 0 gibt an, dass die Antwortvariable überhaupt nicht durch die Prädiktorvariable erklärt werden kann. Ein Wert von 1 gibt an, dass die Antwortvariable perfekt und fehlerfrei durch die Prädiktorvariable erklärt werden kann.
Mit SSR und SST können wir das R-Quadrat wie folgt berechnen:
R im Quadrat = SSR / SST
Wenn beispielsweise der SSR für ein bestimmtes Regressionsmodell 137,5 und der SST 156 beträgt, würden wir das R-Quadrat wie folgt berechnen:
R im Quadrat = 137,5 / 156 = 0,8814
Dies zeigt uns, dass 88,14 % der Variation der Antwortvariablen durch die Prädiktorvariable erklärt werden können.
Berechnen Sie SST, SSR, SSE: Schritt-für-Schritt-Beispiel
Angenommen, wir haben den folgenden Datensatz, der die Anzahl der von sechs verschiedenen Studenten gelernten Stunden zusammen mit ihren Abschlussprüfungsergebnissen zeigt:
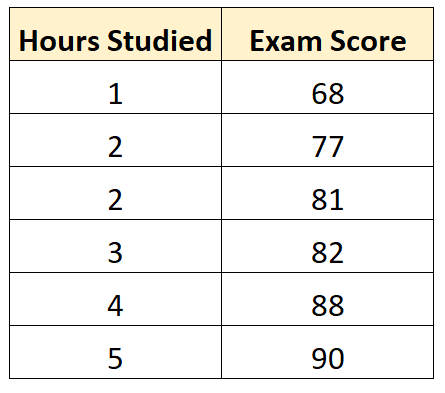
Mit einer Statistiksoftware (wie R , Excel , Python ) oder sogar von Hand können wir sehen, dass die am besten passende Linie ist:
Punktzahl = 66,615 + 5,0769*(Stunden)
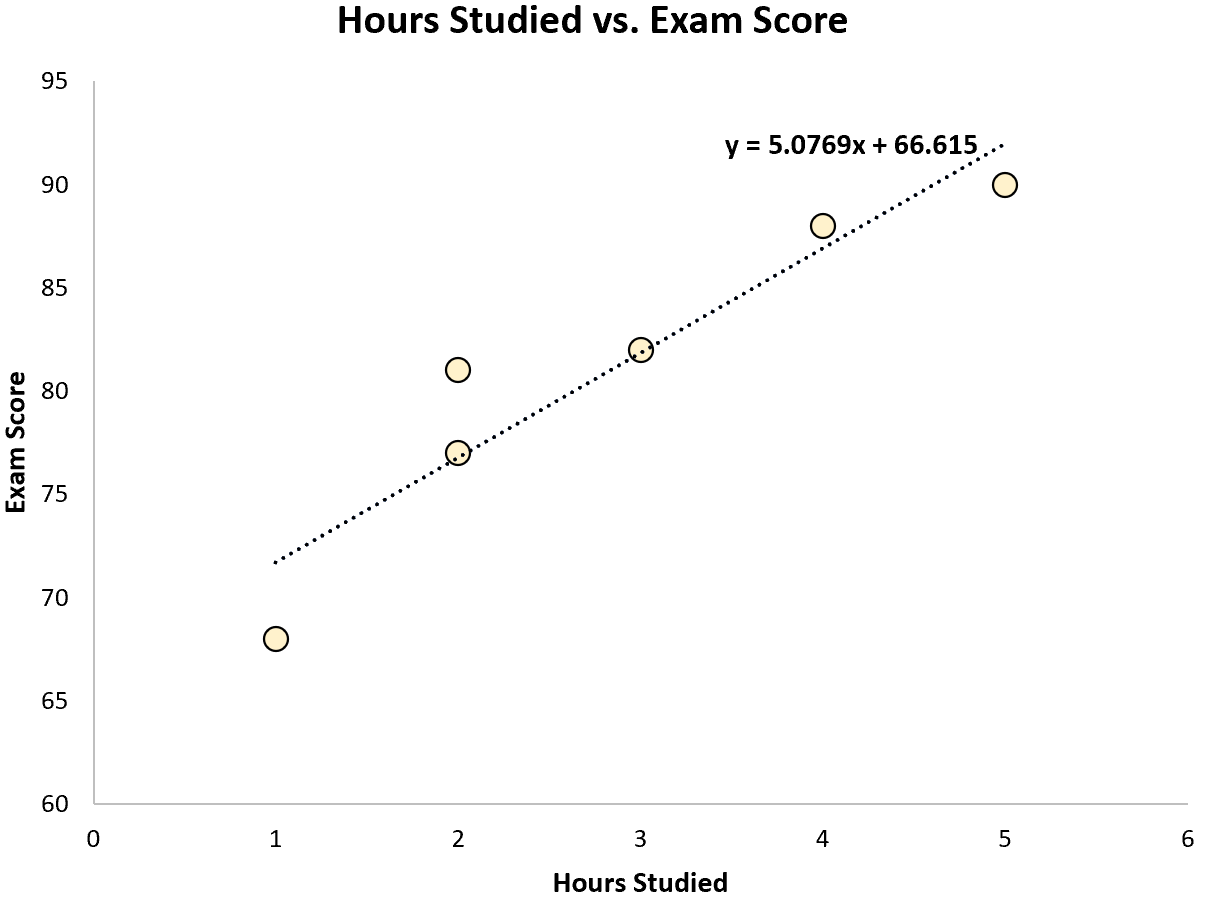
Sobald wir die Linie der am besten passenden Gleichung kennen, können wir die folgenden Schritte verwenden, um SST, SSR und SSE zu berechnen:
Schritt 1: Berechnen Sie den Mittelwert der Antwortvariablen.
Der Mittelwert der Antwortvariablen ( y ) beträgt 81 .
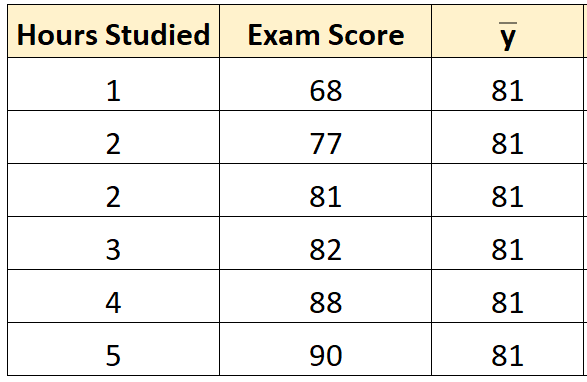
Schritt 2: Berechnen Sie den vorhergesagten Wert für jede Beobachtung.
Dann können wir die Gerade der Best-Fit-Gleichung verwenden, um die vorhergesagte Prüfungspunktzahl () für jeden Schüler zu berechnen.
Die voraussichtliche Prüfungsnote für den Studenten, der eine Stunde gelernt hat, ist beispielsweise:
Punktzahl = 66,615 + 5,0769*(1) = 71,69 .
Wir können den gleichen Ansatz verwenden, um die vorhergesagte Punktzahl für jeden Schüler zu ermitteln:
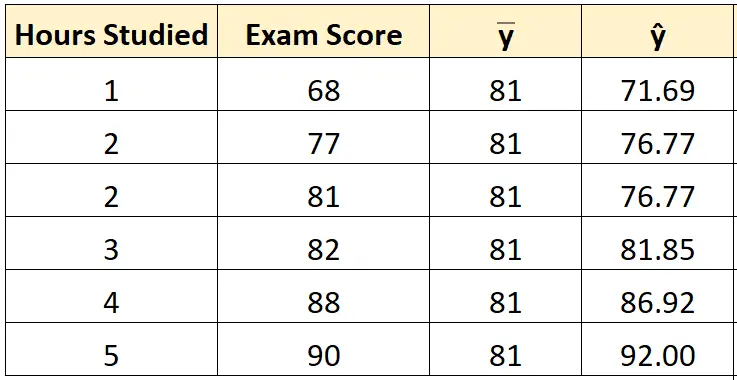
Schritt 3: Berechnen Sie die Gesamtquadratsumme (SST).
Dann können wir die Summe der Quadrate insgesamt berechnen.
Die Gesamtsumme der Quadrate für den ersten Schüler beträgt beispielsweise:
(y i – y ) 2 = (68 – 81) 2 = 169 .
Wir können den gleichen Ansatz verwenden, um die Gesamtsumme der Quadrate für jeden Schüler zu ermitteln:
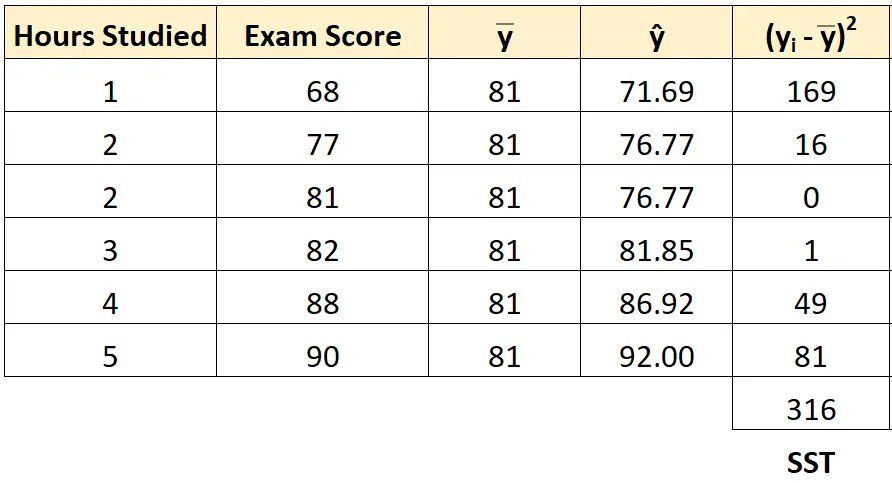
Die Gesamtsumme der Quadrate beträgt 316 .
Schritt 4: Berechnen Sie die Summe der Quadrate-Regression (SSR).
Dann können wir die Summe der Quadrate der Regression berechnen.
Die Summe der Quadrate-Regression für den ersten Schüler lautet beispielsweise:
( ŷi – y ) 2 = (71,69 – 81) 2 = 86,64 .
Wir können denselben Ansatz verwenden, um die Regression der Quadratsumme für jeden Schüler zu ermitteln:
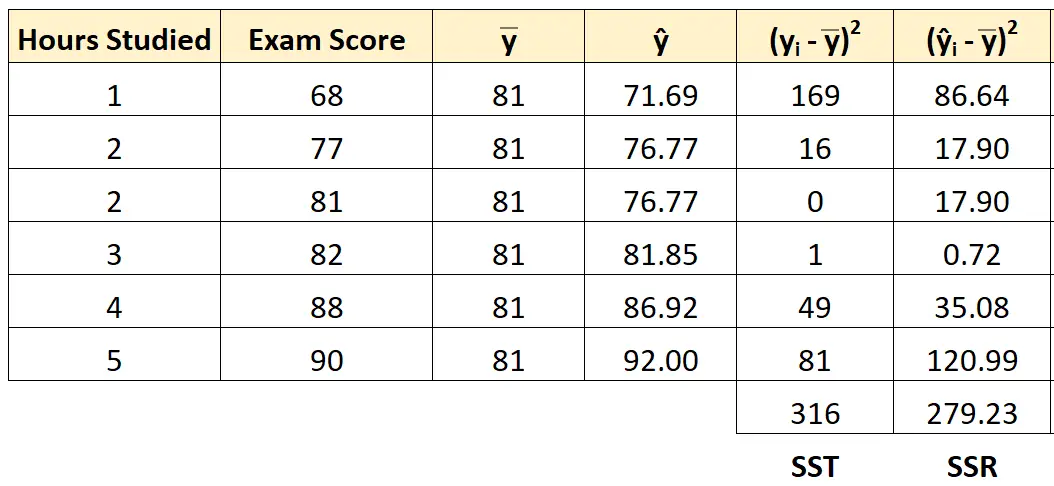
Die Summe der Quadrate der Regression beträgt 279,23 .
Schritt 5: Berechnen Sie die Summe der Fehlerquadrate (SSE).
Dann können wir den Fehler der Quadratsumme berechnen.
Beispielsweise beträgt die Fehlerquadratsumme für den ersten Schüler:
(ŷ i – y i ) 2 = (71,69 – 68) 2 = 13,63 .
Wir können den gleichen Ansatz verwenden, um die Fehlerquadratsumme für jeden Schüler zu ermitteln:
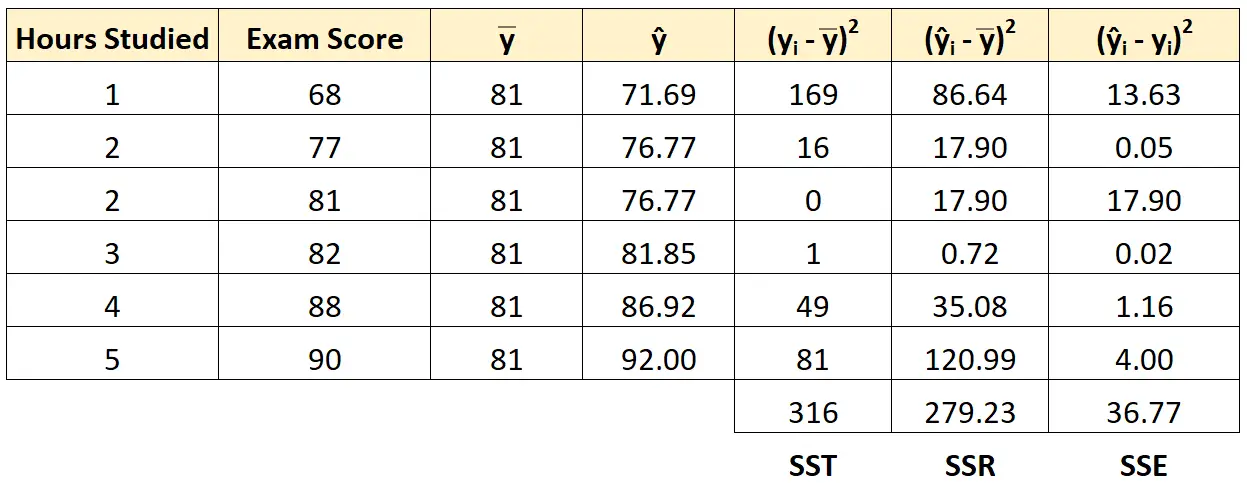
Wir können überprüfen, dass SST = SSR + SSE ist
- SST = SSR + SSE
- 316 = 279,23 + 36,77
Wir können das R-Quadrat des Regressionsmodells auch mithilfe der folgenden Gleichung berechnen:
- R im Quadrat = SSR / SST
- R im Quadrat = 279,23 / 316
- R im Quadrat = 0,8836
Dies zeigt uns, dass 88,36 % der Abweichungen bei den Prüfungsergebnissen durch die Anzahl der gelernten Stunden erklärt werden können.
Zusätzliche Ressourcen
Sie können die folgenden Rechner verwenden, um SST, SSR und SSE für jede einfache lineare Regressionslinie automatisch zu berechnen:
SST-Rechner
RSS-Rechner
ESS-Rechner