So berechnen sie sst, ssr und sse in excel

Wir verwenden oft drei verschiedene Quadratsummenwerte , um zu messen, wie gut eine Regressionslinie tatsächlich zu einem Datensatz passt:

1. Summe der Gesamtquadrate (SST) – Die Summe der Quadrate der Differenzen zwischen einzelnen Datenpunkten (y _i ) und dem Mittelwert der Antwortvariablen ( y ).

• SST = Σ(y _i – y ) ²

2. Summe der Quadrate-Regression (SSR) – Die Summe der Quadrate der Differenzen zwischen den vorhergesagten Datenpunkten (ŷ _i ) und dem Mittelwert der Antwortvariablen ( y ).

• SSR = Σ(ŷ _i – y ) ²

3. Fehlerquadratsumme (SSE) – Die Summe der Quadrate der Differenzen zwischen den vorhergesagten Datenpunkten (ŷ _i ) und den beobachteten Datenpunkten (y _i ).

• SSE = Σ(ŷ _i – y _i ) ²

Das folgende Schritt-für-Schritt-Beispiel zeigt, wie jede dieser Metriken für ein bestimmtes Regressionsmodell in Excel berechnet wird.

Schritt 1: Erstellen Sie die Daten

Erstellen wir zunächst einen Datensatz mit der Anzahl der Lernstunden und den erzielten Prüfungsergebnissen für 20 verschiedene Schüler an einer bestimmten Schule:

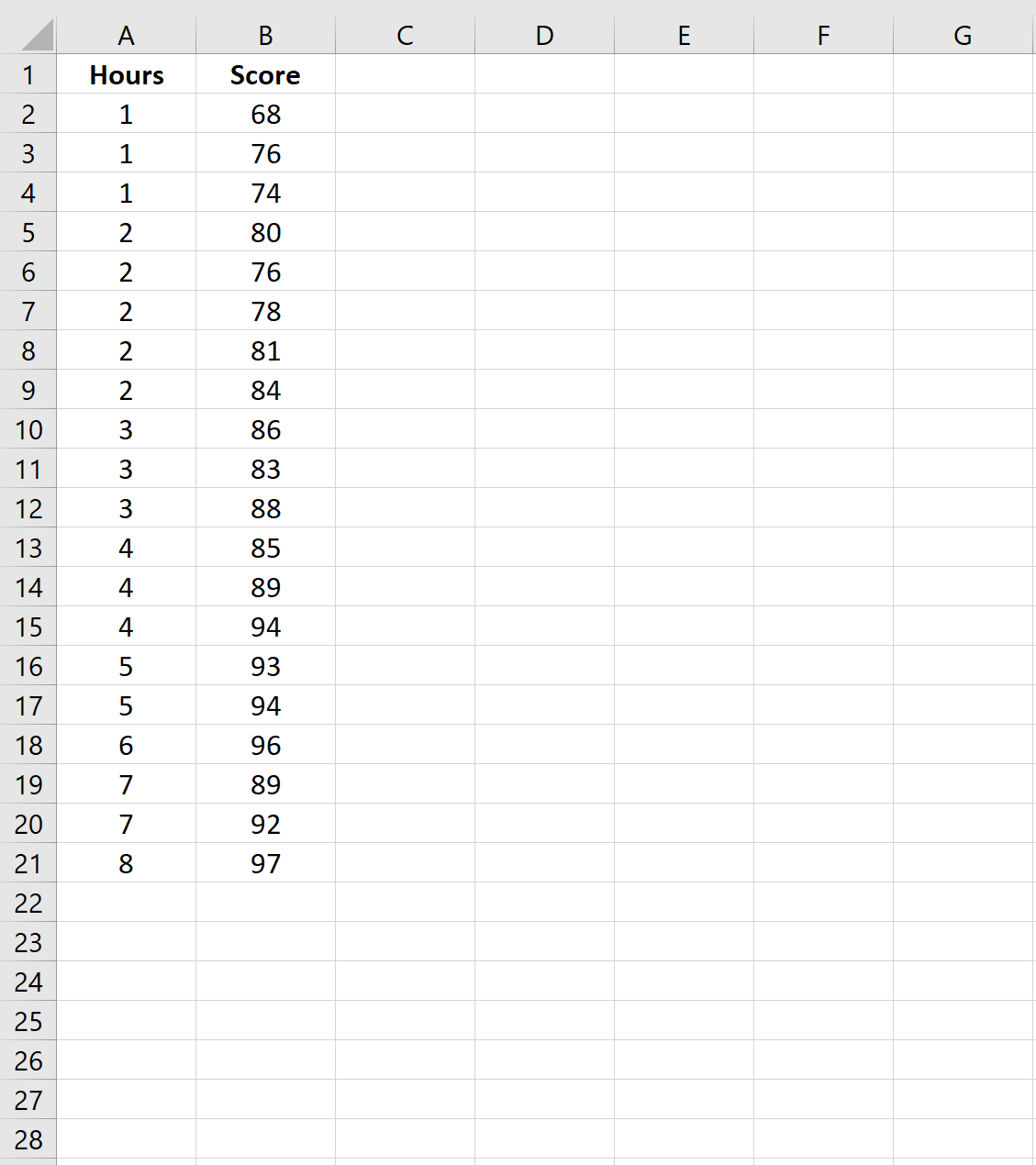
Schritt 2: Passen Sie ein Regressionsmodell an

Klicken Sie im oberen Menüband von Excel auf die Registerkarte „Daten“ und dann auf „Datenanalyse“ . Wenn diese Option nicht angezeigt wird, müssen Sie zunächst die kostenlose Analysis ToolPak-Software installieren .

Sobald Sie auf Datenanalyse klicken, erscheint ein neues Fenster. Wählen Sie Regression und klicken Sie auf OK.

Geben Sie im neuen Fenster, das erscheint, die folgenden Informationen ein:

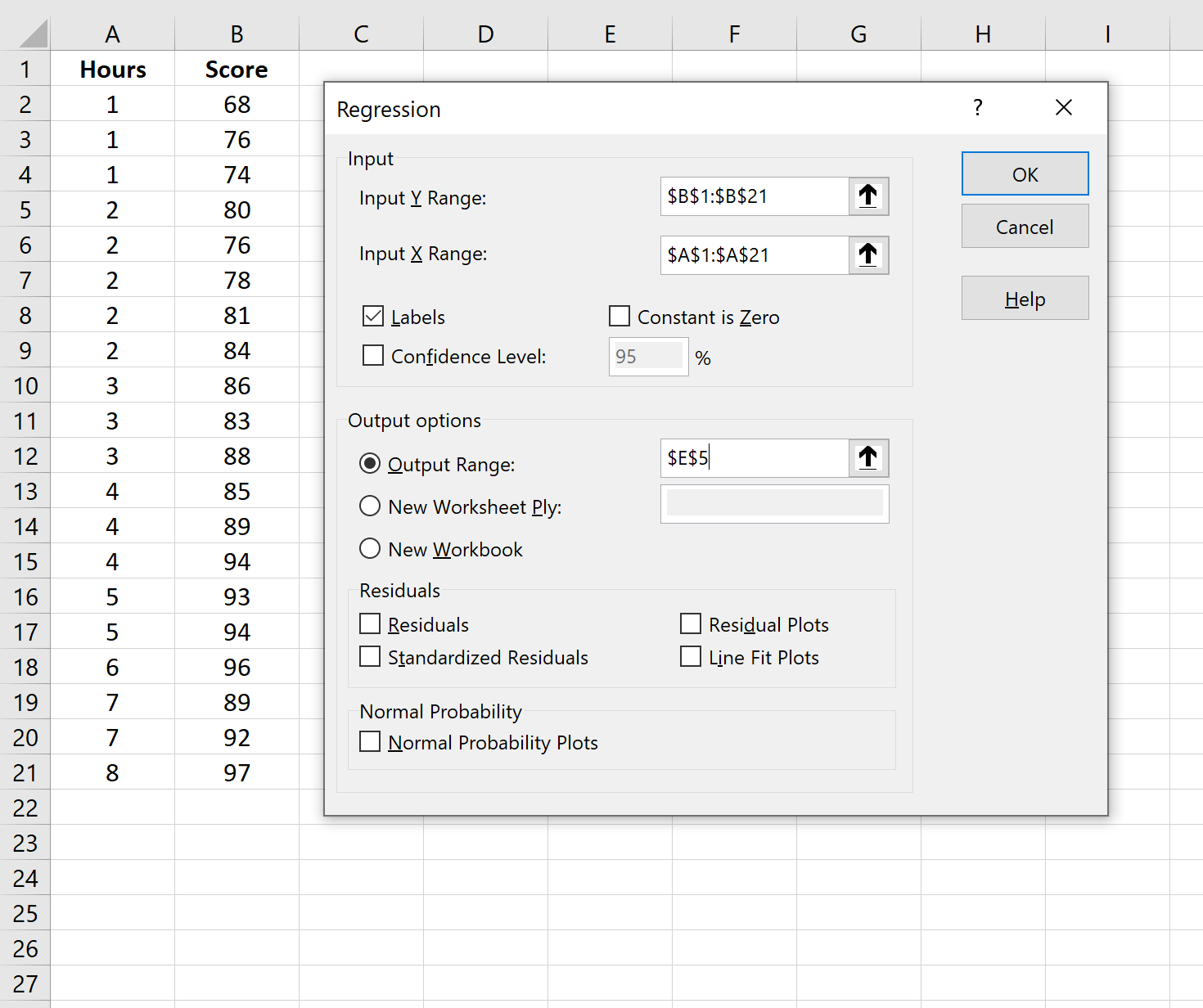
Sobald Sie auf OK klicken, wird die Regressionsausgabe angezeigt.

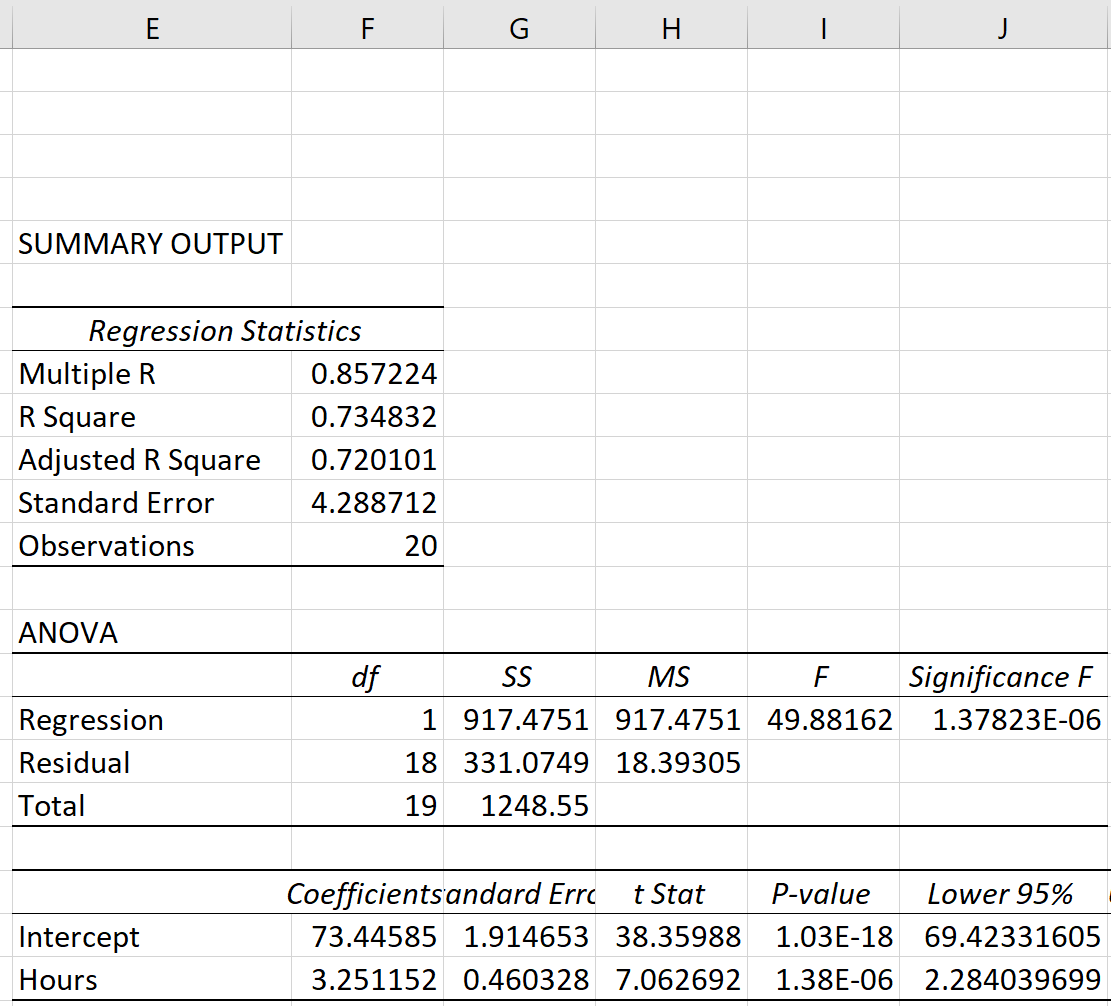
Schritt 3: Analysieren Sie das Ergebnis

Die drei Quadratsummenmetriken – SST, SSR und SSE – sind in der SS- Spalte der ANOVA- Tabelle zu sehen:

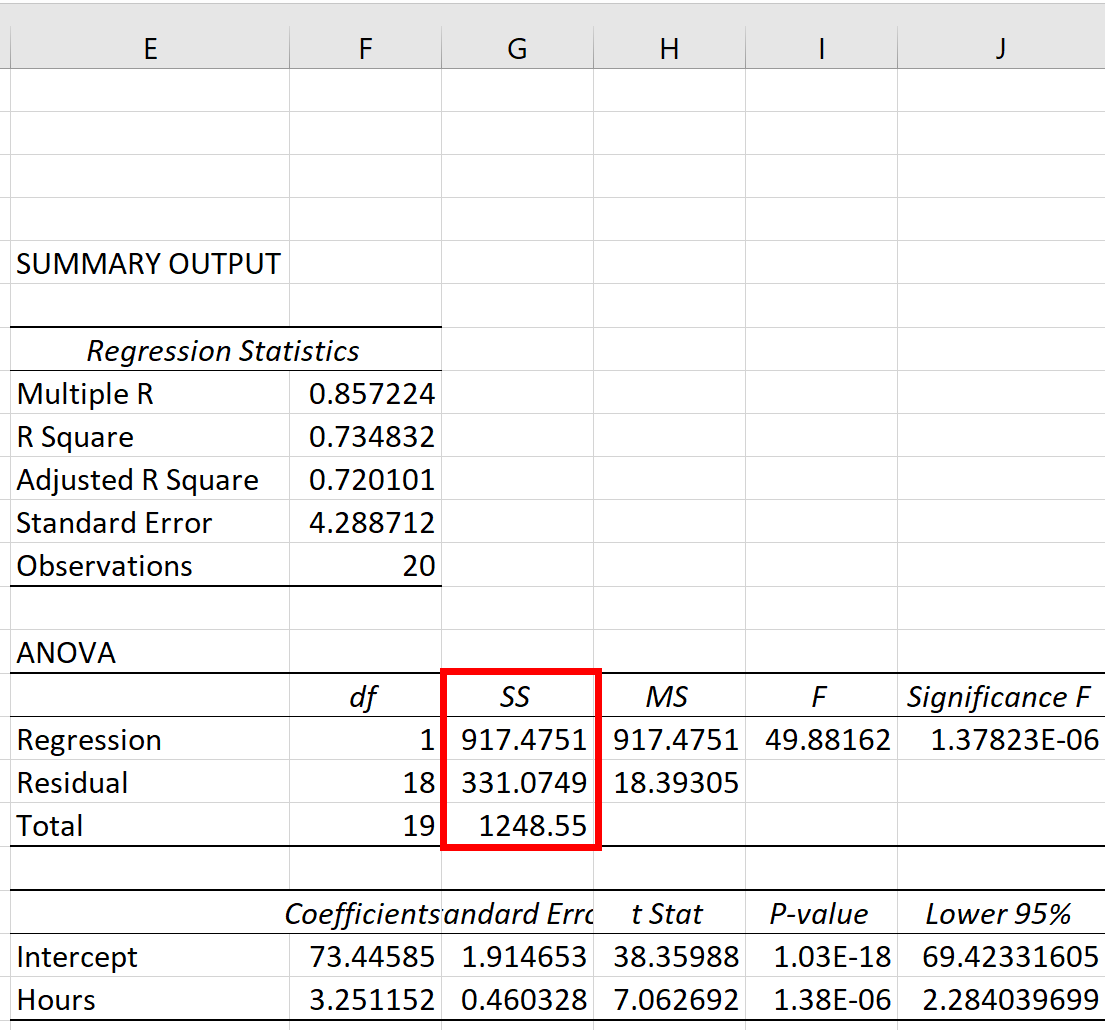
Die Kennzahlen lauten wie folgt:

• Gesamtsumme der Quadrate (SST): 1248,55
• Summe der Quadrate-Regression (SSR): 917,4751
• Fehlerquadratsumme (SSE): 331,0749

Wir können überprüfen, dass SST = SSR + SSE:

• SST = SSR + SSE
• 1248,55 = 917,4751 + 331,0749

Wir können das R-Quadrat des Regressionsmodells auch manuell berechnen:

• R im Quadrat = SSR / SST
• R im Quadrat = 917,4751 / 1248,55
• R im Quadrat = 0,7348

Dies zeigt uns, dass 73,48 % der Abweichungen bei den Prüfungsergebnissen durch die Anzahl der gelernten Stunden erklärt werden können.

Zusätzliche Ressourcen

So führen Sie eine einfache lineare Regression in Excel durch
So führen Sie eine multiple lineare Regression in Excel durch
So führen Sie eine Polynomregression in Excel durch
So führen Sie eine exponentielle Regression in Excel durch