Stamm- und blattdiagramm

In diesem Artikel wird erläutert, was Stamm- und Blattdiagramme in der Statistik sind und wofür sie verwendet werden. Sie erfahren daher, wie Sie ein Stamm-Blatt-Diagramm erstellen, lösen Übungen für diese Art von statistischen Diagrammen und erfahren schließlich, welche Vor- und Nachteile das Stamm-Blatt-Diagramm hat.

Was ist das Stamm-Blatt-Diagramm?

Das Stamm- und Blattdiagramm ist eine Art statistisches Diagramm, in dem eine Reihe quantitativer Daten dargestellt wird.

In einem Stamm-Blatt-Diagramm wird jeder Datenpunkt durch das Blatt (die letzte Ziffer) und den Stamm (die übrigen Ziffern) getrennt. In einem Stängel-Blatt-Diagramm wird also jedes Blatt auf der Linie seines entsprechenden Stängels platziert.

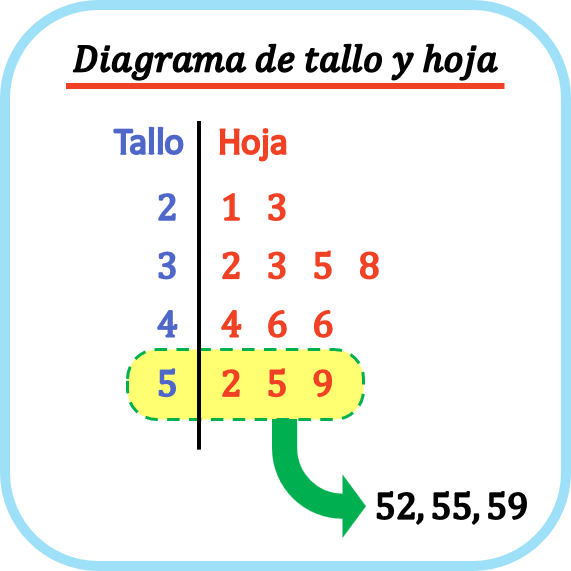
Auf diese Weise helfen Stamm- und Blattdiagramme dabei, einen Satz statistischer Daten grafisch darzustellen und auch die Form der Verteilung zu visualisieren.

Das Stamm-Blatt-Diagramm ist auch als Stamm-Blatt-Diagramm bekannt, ein Name, der aus dem Englischen stammt.

Die Stamm- und Blattdarstellung ist dem Histogramm sehr ähnlich, obwohl diese andere Art von statistischem Diagramm für größere Stichprobengrößen verwendet wird.

So erstellen Sie ein Stamm- und Blattdiagramm

Gehen Sie folgendermaßen vor , um ein Stamm- und Blattdiagramm zu erstellen :

1. Sortieren Sie die Daten vom kleinsten zum größten.
2. Runden Sie ggf. die Zahlen, bis sie die gewünschte Stellenzahl haben.
3. Entscheiden Sie, in welcher Figur der Schnitt zwischen Stängel und Blatt erfolgen soll, d. h. bestimmen Sie die Anzahl der Figuren, die die Blätter haben sollen. Normalerweise ist das Blatt so gestaltet, dass es nur die letzte Ziffer jedes Datenelements enthält.
4. Stellen Sie alle Daten im Stamm- und Blattdiagramm dar. Die Stängel werden in aufsteigender Reihenfolge in der linken Spalte platziert, während die Blätter in der rechten Spalte auf der Höhe ihres entsprechenden Stängels und ebenfalls in aufsteigender Reihenfolge platziert werden.

Beispiel für ein Stamm- und Blattdiagramm

Damit Sie sehen können, wie Sie ein Stamm- und Blattdiagramm erstellen, lösen wir unten zwei Beispiele: eines ohne Dezimalstellen und eines mit Dezimalstellen.

Beispiel 1

• Zeichnen Sie die folgenden Datenreihen in ein Stamm- und Blattdiagramm ein:

In diesem Fall sind die Daten bereits geordnet und gerundet, sodass diese beiden Schritte nicht erforderlich sind. Da Zahlen also zweistellig sind, werden sie so dargestellt, dass die Zeiten den Stamm und die Einsen die Blätter des Graphen bilden.

Wir werden zunächst den Stamm des Diagramms darstellen. Die Zeitform der Daten geht bis 9, also erstellen wir für jede Zehn eine Linie:

Und dann stellen wir die Blätter dar, dazu platzieren wir die Einheit jedes Datenwerts in der entsprechenden Zeile. Zum Beispiel geht die Zahl 57 zur Wurzel 5 und in der rechten Spalte fügen wir eine 7 hinzu.

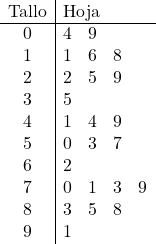
Und auf diese Weise wurden alle Probendaten in einem Stamm- und Blattdiagramm dargestellt.

Beispiel 2

• Vergleichen Sie die folgenden zwei Datenbeispiele mithilfe eines Stamm-Blatt-Diagramms mit Dezimalzahlen.

Wie Sie in dieser Übung sehen werden, kann ein einzelnes Stamm-Blatt-Diagramm zur Darstellung zweier statistischer Stichproben verwendet werden. Daher werden wir beide Datensätze im selben Stamm-Blatt-Diagramm darstellen: einen links und einen rechts. Diese Art von Parzelle wird als doppelstämmige Stamm-Blatt-Parzelle bezeichnet.

In diesem Fall nehmen wir den ganzen Teil der Zahlen als Stamm des Diagramms und die Dezimalstellen hingegen als Blätter des Diagramms. Wir konstruieren daher das Stamm- und Blattlayout, indem wir alle ganzen Teile platzieren:

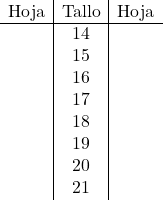
Und jetzt platzieren wir das Blatt aller Daten in dem dazugehörigen Stamm:

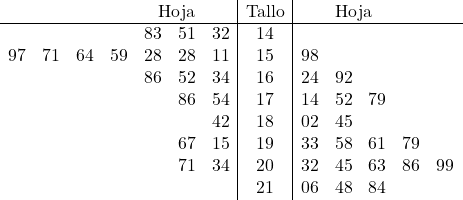
Durch die grafische Darstellung der Daten können wir sie leicht vergleichen. Insbesondere sehen wir, dass die Stichprobendaten auf der rechten Seite etwas größer sind als die Stichproben auf der linken Seite, daher wird auch ihr Durchschnitt größer sein. Abhängig vom Ziel der statistischen Studie werden wir daher daran interessiert sein, diese oder jene Stichprobe auszuwählen.

Bedenken Sie, dass Sie nicht nur wissen müssen, wie man ein Slash-and-Blade-Diagramm erstellt, sondern auch wissen müssen, wie man das Diagramm interpretiert.

Vor- und Nachteile des Stamm- und Blattdiagramms

Aufgrund der Eigenschaften der Stamm- und Blattparzelle haben diese Parzellentypen folgende Vor- und Nachteile:

Vorteil:

• Wenn Sie die Stängel und Blätter verfolgen, können Sie die Form einer Verteilung erkennen.
• Mit dem Doppelstamm-Stamm-Blatt-Diagramm können zwei Verteilungen verglichen werden.
• Damit können Sie Ausreißer in einem Datensatz schnell identifizieren.
• Sie können den Modus der Datenreihe mit dem Auge bestimmen.

Nachteile:

• Das Stamm- und Blattdiagramm wird immer seltener verwendet, da Computersoftware schnell ein komplexeres Diagramm erstellen kann.
• Die darzustellende Stichprobengröße ist begrenzt und liegt im Allgemeinen zwischen 15 und 150 Datenpunkten.
• Es können nur quantitative Daten dargestellt werden.