So erstellen sie ein stamm- und blattdiagramm mit dezimalzahlen

Ein Stamm- und Blattdiagramm ist eine Art Diagramm, das Daten anzeigt, indem jeder Wert in einem Datensatz in einen „Stamm“ und ein „Blatt“ unterteilt wird.

Angenommen, wir haben den folgenden Datensatz:

Datensatz: 12, 14, 18, 22, 22, 23, 25, 25, 28, 45, 47, 48

Wenn wir die erste Ziffer jedes Werts als „Stamm“ und die zweite Ziffer als „Blatt“ definieren, können wir das folgende Stamm- und Blattdiagramm erstellen:

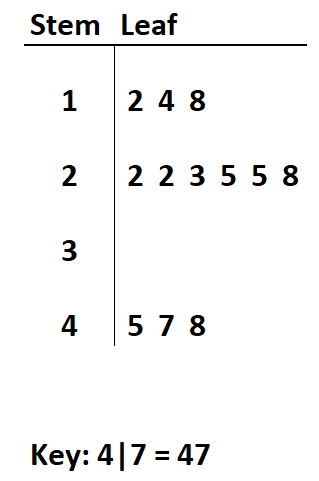
Obwohl Stamm- und Blattdiagramme normalerweise mit ganzzahligen Werten verwendet werden, können sie auch für Werte mit Dezimalstellen verwendet werden.

Die folgenden Beispiele veranschaulichen, wie Stamm- und Blattdiagramme mit Dezimalzahlen erstellt werden.

Beispiel 1: Stamm- und Blattdiagramm mit einer Dezimalstelle

Angenommen, wir haben den folgenden Datensatz:

Datensatz: 11.6, 12.2, 12.5, 12.6, 13.7, 13.8, 14.1, 15.2

Wenn wir die Zahlen vor dem Komma als Stamm und die Zahlen nach dem Komma als Blatt definieren, können wir das folgende Stamm- und Blattdiagramm erstellen:

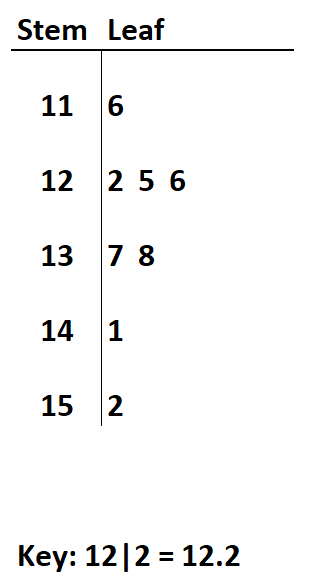
Beim Erstellen dieses Stamm- und Blattdiagramms ist es wichtig, unten einen Schlüssel einzufügen, damit der Leser weiß, wie die Stamm- und Blattwerte zu interpretieren sind.

Beispiel 2: Stamm- und Blattdiagramm mit mehreren Dezimalstellen

Angenommen, wir haben den folgenden Datensatz:

Datensatz: 3,26, 3,28, 3,34, 3,38, 3,41, 3,42, 3,44, 3,59, 3,63

Wenn wir die Ganzzahl und den ersten Wert nach der Dezimalstelle als Stamm und den zweiten Wert nach der Dezimalstelle als Blatt festlegen, können wir das folgende Stamm- und Blattdiagramm erstellen:

Auch hier zeigt uns der Schlüssel am unteren Rand des Diagramms, wie die Diagrammwerte zu interpretieren sind.

Beispiel 3: Interpretation eines Stamm- und Blattdiagramms mit Dezimalzahlen

Angenommen, wir haben das folgende Stamm- und Blattdiagramm mit Dezimalstellen:

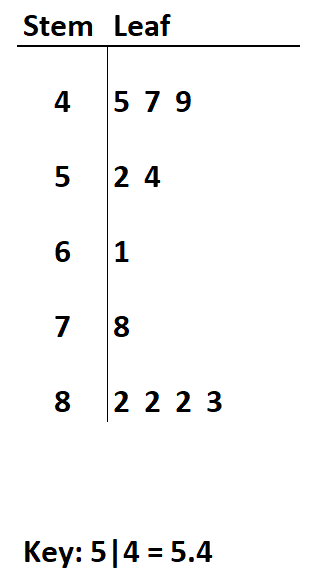
Frage 1: Was ist der Maximalwert im Datensatz?

Der Maximalwert wäre 8,3 .

Frage 2: Welchen Umfang hat der Datensatz?

Der Bereich des Datensatzes ist die Differenz zwischen dem größten und dem kleinsten Wert. Der Bereich wäre also 8,3 – 4,5 = 3,8 .

Frage 3: Welchen Modus hat der Datensatz?

Der Modus ist der Wert, der am häufigsten erscheint. Das wären 8,2 .

Frage 4: Was ist der Median des Datensatzes?

Der Median ist definiert als der „durchschnittliche“ Wert des Datensatzes. Um diesen Wert zu finden, können wir jeden der einzelnen Werte in den Datensatz schreiben und den Medianwert ermitteln:

Datensatz: 4.5, 4.7, 4.9, 5.2, 5.4, 6.1 , 7.8, 8.2, 8.2, 8.2, 8.3

Der Median liegt bei 6,1 .

Zusätzliche Ressourcen

Eine Einführung in Stamm- und Blattdiagramme
Eine Einführung in aufeinanderfolgende Stamm- und Blattdiagramme
Generator für Stamm- und Blattdiagramme
So erstellen Sie ein Stamm- und Blattdiagramm in Excel