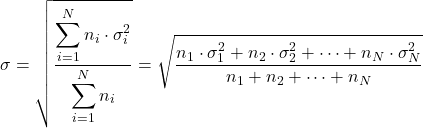Standardabweichung (oder standardabweichung)

Von Dr. Benjamin Anderson August 5, 2023 Statistiken Keine Kommentare

In diesem Artikel wird erklärt, was Standardabweichung, auch Standardabweichung genannt, ist. Sie erfahren, wie Sie die Standardabweichung berechnen, ein praktisches Schritt-für-Schritt-Beispiel und einen Online-Rechner zum Ermitteln der Standardabweichung jeder Datenstichprobe.

Was ist die Standardabweichung (oder Standardabweichung)?

Die Standardabweichung , auch Standardabweichung genannt, ist ein Maß für die statistische Streuung. Mit anderen Worten: Die Standardabweichung ist ein Wert, der die Streuung eines Satzes statistischer Daten angibt.

Daher wird die Standardabweichung (oder Standardabweichung) verwendet, um die Streuung einer Grundgesamtheit oder statistischen Stichprobe zu quantifizieren. Je größer die Standardabweichung einer Datenreihe ist, desto stärker sind die Daten gestreut. Und die Interpretation kann auch in die andere Richtung erfolgen: Wenn die Standardabweichung gering ist, bedeutet dies, dass die Daten im Allgemeinen sehr nahe an ihrem Mittelwert liegen.

Bei der Berechnung der Standard- oder typischen Abweichung über eine Grundgesamtheit ist das Symbol für die Standardabweichung der griechische Buchstabe Sigma (σ). Wenn es jedoch um die Stichprobenstandardabweichung geht, wird der Buchstabe s verwendet, um die statistische Messung darzustellen.

In manchen Statistik- und Wahrscheinlichkeitsbüchern wird die Standardabweichung auch als Standardabweichung bezeichnet.

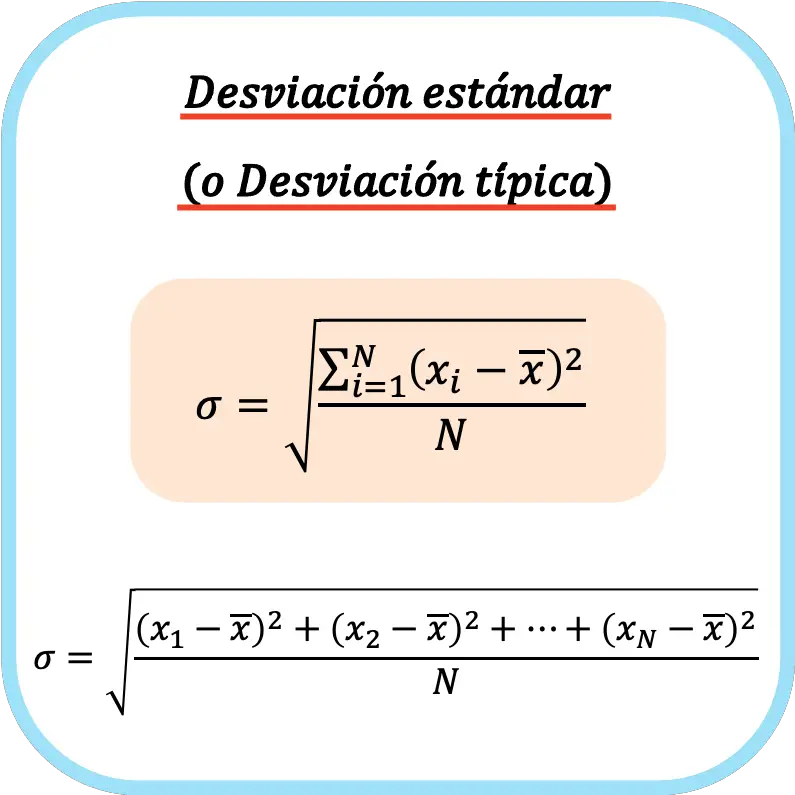
Formel für die Standardabweichung (oder Standardabweichung).

Die Standardabweichung (oder Standardabweichung) ist gleich der Quadratwurzel der Summe der Quadrate der Abweichungen der Datenreihe dividiert durch die Gesamtzahl der Beobachtungen.

Die Formel zur Berechnung der Standardabweichung (bzw. Standardabweichung) lautet daher:

👉 Mit dem Rechner unten können Sie die Standardabweichung eines beliebigen Datensatzes berechnen.

Um die Standardabweichung eines Datensatzes zu ermitteln, müssen Sie abschließend alle Abweichungen berechnen (definiert als die Differenz zwischen einem Datenpunkt und dem arithmetischen Mittel), die Abweichungen auf zwei erhöhen, sie alle addieren und dann durch dividieren gesamt. Anzahl der Daten und ziehen Sie schließlich die Quadratwurzel.

Beispiel für Standardabweichung (oder Standardabweichung)

In Anbetracht der Definition der Standardabweichung (oder typischen Abweichung) finden Sie unten ein Schritt-für-Schritt-Beispiel, damit Sie sehen können, wie die Standardabweichung einer Datenreihe berechnet wird.

Berechnen Sie die Standardabweichung der folgenden Werte: 3, 6, 2, 9, 4.

Als erstes müssen wir den Stichprobenmittelwert bestimmen. Dazu addieren wir alle Daten und dividieren durch die Gesamtzahl der Beobachtungen, also fünf:

$\overline{x}=\cfrac{3+6+2+9+4}{5}=4,8$

Wir verwenden jetzt die Standardabweichungsformel:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N(x_i-\overline{x})^2}{N}}$

Wir setzen die Daten in die Formel ein:

$\displaystyle\sigma =\sqrt{\frac{(3-4,8)^2+(6-4,8)^2+(2-4,8)^2+(9-4,8)^2+(4-4,8)^2}{5}}$

Und schließlich berechnen wir die Standardabweichung:

$\begin{aligned}\displaystyle\sigma & = \sqrt{\frac{(-1,8)^2+1,2^2+(-2,8)^2+4,2^2+(-0,8)^2}{5}}\\[2ex]&=\sqrt{\frac{3,24+1,44+7,84+17,64+0,64}{5}}\\[2ex]&= \sqrt{\frac{30,8}{5}}=\sqrt{6,16}=2,48 \end{aligned}$

Standardabweichungsrechner (oder Standardabweichungsrechner).

Geben Sie einen Satz statistischer Daten in den folgenden Online-Rechner ein, um die Standardabweichung (oder Standardabweichung) zu berechnen. Die Daten müssen durch ein Leerzeichen getrennt und mit dem Punkt als Dezimaltrennzeichen eingegeben werden.

Standardabweichung (oder typische Abweichung) für gruppierte Daten

Um die Standardabweichung (oder Standardabweichung) von in Intervallen gruppierten Daten zu berechnen , müssen die folgenden Schritte befolgt werden:

Ermitteln Sie den Mittelwert der gruppierten Daten.
Berechnen Sie Abweichungen gruppierter Daten.
Füllen Sie jede Lücke aus.
Multiplizieren Sie jedes vorherige Ergebnis mit der Häufigkeit seines Intervalls.
Addieren Sie die Summe aller im vorherigen Schritt erhaltenen Werte.
Teilen Sie durch die Gesamtzahl der Beobachtungen.
Ziehen Sie die Quadratwurzel aus dem vorherigen Wert. Die resultierende Zahl ist die Standardabweichung der gruppierten Daten.

Zusammenfassend lautet die Formel zur Berechnung der Standardabweichung von in Intervallen gruppierten Daten:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N\left(x_i-\overline{x}\right)^2\cdot f_i }{N}}$

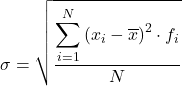
Obwohl normalerweise die obige Formel verwendet wird, kann auch der folgende algebraische Ausdruck verwendet werden, da das gleiche Ergebnis erzielt wird:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^n x_i^2\cdot f_i }{N}-\overline{x}^2}$

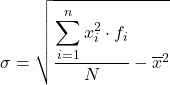
Damit Sie sehen können, wie das geht, finden Sie unten eine Schritt-für-Schritt-Übung zur Standardabweichung von in Intervallen gruppierten Daten. Genauer gesagt wird die Standardabweichung der folgenden statistischen Daten berechnet:

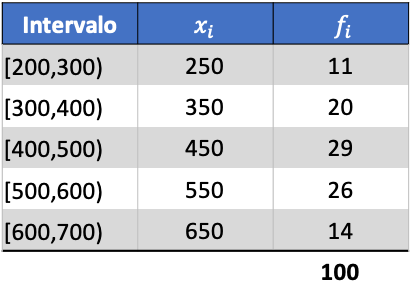
Beispiel für in Intervalle gruppierte Daten

Zunächst multiplizieren wir den Klassenwert jedes Intervalls mit seiner Häufigkeit, um das arithmetische Mittel zu berechnen:

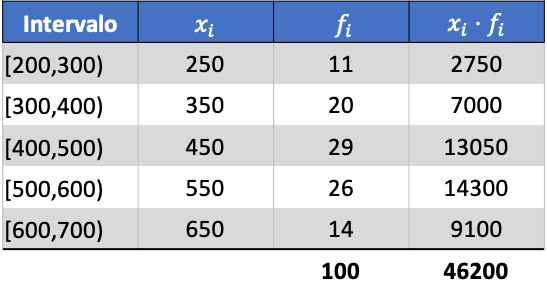
Der Durchschnitt der gruppierten Daten beträgt also:

$\overline{x}=\cfrac{\displaystyle\sum_{i=1}^n x_i\cdot f_i}{N}=\cfrac{46200}{100}=462$

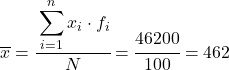
Nachdem wir nun den Wert des Durchschnitts kennen, müssen wir der Datentabelle die folgenden drei Spalten hinzufügen:

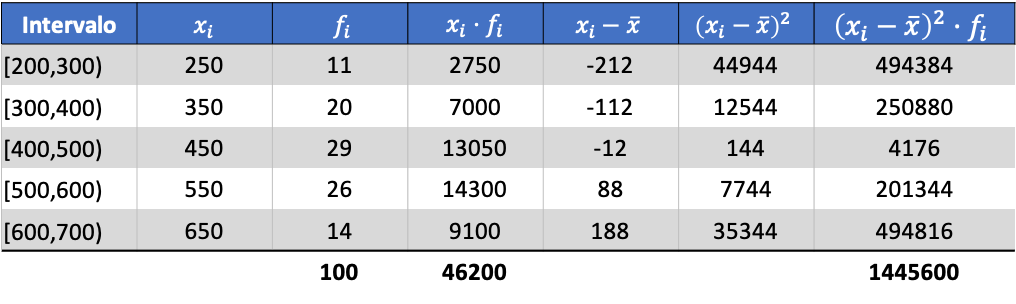
Übung zur Standardabweichung bzw. Standardabweichung für gruppierte Daten gelöst

Dann ist die Standardabweichung der gruppierten Daten das Ergebnis der Quadratwurzel des Gesamtwerts der letzten Spalte dividiert durch die Gesamtzahl der Beobachtungen:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N\left(x_i-\overline{x}\right)^2\cdot f_i }{N}}=\sqrt{\frac{1445600}{100}}=120,23$

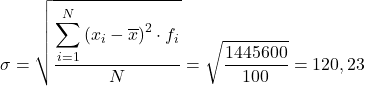
Standardabweichung (oder typische Abweichung) und Varianz

Die Beziehung zwischen Standardabweichung (oder typischer Abweichung) und Varianz besteht darin, dass die Standardabweichung die Quadratwurzel der Varianz ist.

Wenn wir also den Varianzwert eines Datensatzes kennen, können wir die Standardabweichung leicht berechnen, indem wir die Quadratwurzel ziehen. Oder umgekehrt: Wenn wir die Standardabweichung kennen, können wir die Varianz durch Quadrieren des Wertes ermitteln.

$Var(X)=\sigma^2$

Tatsächlich kann die Varianz einfach durch die Verwendung des Quadrats der Standardabweichung dargestellt werden. Daher ist das Symbol für die Populationsvarianz das Sigma-Quadrat (σ ² ) und das Symbol für die Stichprobenvarianz das s-Quadrat (s ² ).

Darüber hinaus werden die Konzepte Standardabweichung und Varianz ähnlich interpretiert, da beide die Streuung einer Reihe statistischer Daten zeigen.

Eigenschaften der Standardabweichung (oder Standardabweichung)

Die Standardabweichung hat folgende Eigenschaften:

Die Standardabweichung einer Datenstichprobe darf nicht negativ sein.

$\sigma \ge 0$

Die Standardabweichung beträgt Null, wenn alle Daten gleich sind.

$\sigma =0$

Wenn allen Daten ein konstanter Term hinzugefügt wird, ändert sich der Standardabweichungswert nicht.

$\sigma (X+k)=\sigma (X)$

Wenn alle Daten mit einer Zahl multipliziert werden, wird die Standardabweichung mit dem Absolutwert dieser Zahl multipliziert.

$\sigma (k\cdot X)=|k|\cdot \sigma (X)$

Die Standardabweichung der Summe zweier Zufallsvariablen ist gleich der Quadratwurzel der Summe der Varianzen der Variablen plus dem Doppelten der Kovarianz zwischen den beiden Variablen.

$\sigma(X+Y)=\sqrt{Var(X)+Var(Y)+2\cdot Cov(X,Y)}$

Wenn wir die Standardabweichungen der verschiedenen Verteilungen (σ _i ) und ihre Datenanzahl (n _i ) kennen, können wir die Gesamtstandardabweichung berechnen, indem wir die folgende Formel anwenden:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle \sum_{i=1}^N n_i\cdot \sigma_i^2}{\displaystyle \sum_{i=1}^N n_i}}=\sqrt{\frac{\displaystyle n_1\cdot \sigma_1^2+n_2\cdot \sigma_2^2+\dots +n_N\cdot \sigma_N^2}{\displaystyle n_1+n_2+\dots+n_N}}$

Über den Autor

Dr. Benjamin Anderson

Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen