So interpretieren sie eine standardabweichung von null
In der Statistik wird die Standardabweichung verwendet, um die Verteilung von Werten in einer Stichprobe zu messen.
Mit der folgenden Formel können wir die Standardabweichung einer bestimmten Stichprobe berechnen:
√ Σ(x i – x bar ) 2 / (n-1)
Gold:
- Σ: Ein Symbol, das „Summe“ bedeutet
- x i : der i-te Wert der Stichprobe
- x bar : Der Stichprobenmittelwert
- n: Die Stichprobengröße
Je höher der Standardabweichungswert ist, desto stärker sind die Werte in einer Stichprobe gestreut.
Je niedriger der Standardabweichungswert ist, desto enger sind die Werte gruppiert.
Wenn die Standardabweichung einer Stichprobe Null ist, bedeutet dies, dass alle Werte in der Stichprobe genau gleich sind.
Mit anderen Worten: Es gibt keine Lücke zwischen den Werten.
Das folgende Beispiel zeigt, wie eine Standardabweichung von Null in der Praxis interpretiert wird.
Beispiel: So interpretieren Sie eine Standardabweichung von Null
Angenommen, wir sammeln eine einfache Zufallsstichprobe von 10 Eidechsen und messen ihre Länge (in Zoll):
Längen : 7, 7, 7, 7, 7, 7, 7, 7, 7, 7
Die durchschnittliche Länge der Eidechsen in der Stichprobe beträgt 7 Zoll.
Mit diesem Wissen können wir die Stichprobenstandardabweichung(en) für diesen Datensatz berechnen:
- s = √ Σ(x i – x bar ) 2 / (n-1)
- s = √ ((7 – 7) 2 + (7 – 7) 2 + (7 – 7) 2 + … + (7 – 7) 2 / (10-1)
- s = √ 0 2 + 0 2 + 0 2 + … + 0 2 / 9
- s = 0
Die Standardabweichung der Stichprobe beträgt 0 .
Da jede Eidechse genau die gleiche Länge hat, ist die Werteverteilung im Datensatz genau Null.
Wird die Standardabweichung in der realen Welt jemals Null sein?
Es ist durchaus möglich, dass ein Datensatz aus der realen Welt eine Standardabweichung von Null aufweist, aber das kommt selten vor.
Das wahrscheinlichste Szenario, in dem Sie auf eine Standardabweichung von Null stoßen könnten, wäre die Sammlung kleiner Stichproben für seltene Ereignisse.
Angenommen, Sie sammeln Daten über die Anzahl der Verkehrsunfälle über einen Zeitraum von einer Woche in einer bestimmten Stadt.
Es ist durchaus möglich, dass Sie folgende Daten erheben:
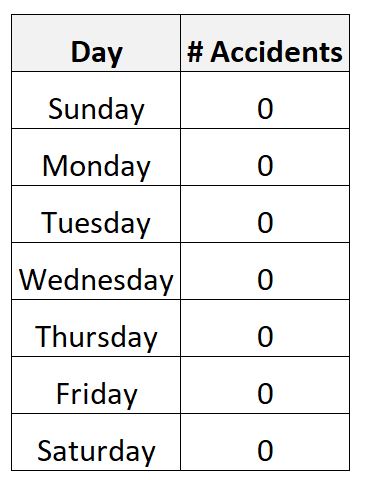
In diesem Szenario wäre die durchschnittliche Zahl der täglichen Unfälle Null und die Standardabweichung wäre ebenfalls Null.
Oder vielleicht erfassen Sie die folgenden Daten über die Anzahl der monatlichen Verkäufe eines teuren Produkts für ein Unternehmen über einen Zeitraum von 6 Monaten:
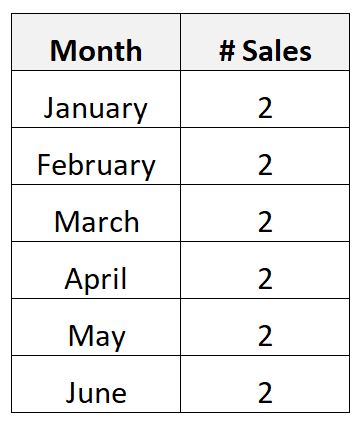
Weil das Produkt so teuer ist, stellt sich heraus, dass das Unternehmen nur genau zwei pro Monat verkauft.
In diesem Szenario beträgt die durchschnittliche Anzahl der monatlich verkauften Produkte zwei und die Standardabweichung der monatlich verkauften Produkte beträgt Null.
Wenn Sie in einem realen Datensatz auf eine Standardabweichung von Null stoßen, wissen Sie einfach, dass dies bedeutet, dass jeder Wert im Datensatz genau gleich ist.
Zusätzliche Ressourcen
Die folgenden Tutorials bieten zusätzliche Informationen zur Standardabweichung in der Statistik:
Warum ist die Standardabweichung wichtig?
Standardabweichung und Standardfehler: Was ist der Unterschied?
Standardabweichung und Interquartilbereich: Was ist der Unterschied?
Über den Autor
Dr. Benjamin Anderson
Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen