Standardabweichung und standardfehler: was ist der unterschied?

Zwei Begriffe, die Studierende in der Statistik häufig verwechseln, sind Standardabweichung und Standardfehler .

Die Standardabweichung misst die Verteilung von Werten in einem Datensatz.

Der Standardfehler ist die Standardabweichung des Mittelwerts wiederholter Stichproben aus einer Grundgesamtheit.

Schauen wir uns ein Beispiel an, um diese Idee klar zu veranschaulichen.

Beispiel: Standardabweichung versus Standardfehler

Angenommen, wir messen das Gewicht von 10 verschiedenen Schildkröten.

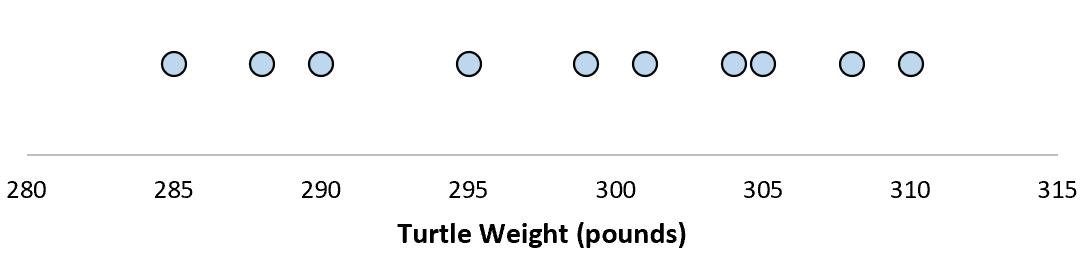
Für diese Stichprobe von 10 Schildkröten können wir den Stichprobenmittelwert und die Stichprobenstandardabweichung berechnen:

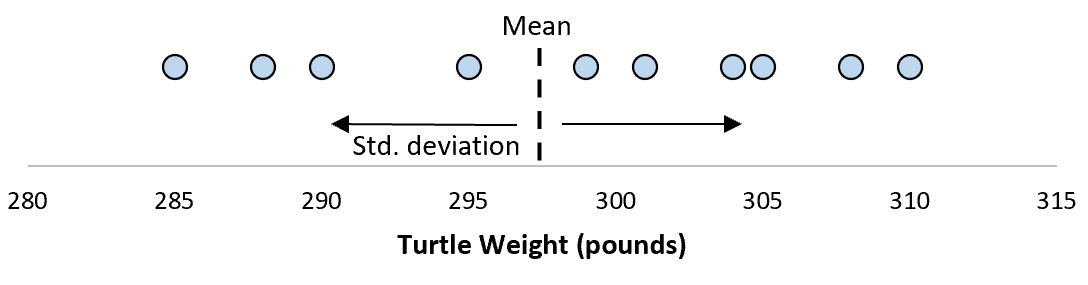
Gehen Sie davon aus, dass die Standardabweichung 8,68 beträgt. Dies gibt uns eine Vorstellung von der Gewichtsverteilung dieser Schildkröten.

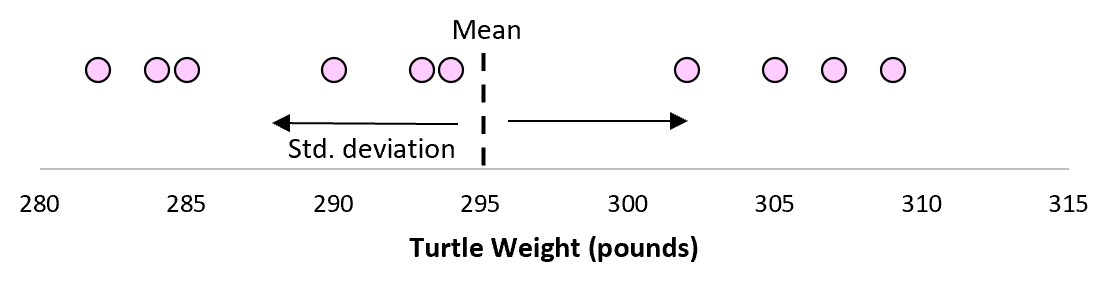
Aber nehmen wir an, wir sammeln eine weitere einfache Zufallsstichprobe von 10 Schildkröten und nehmen auch deren Messungen vor.

Es ist mehr als wahrscheinlich, dass diese Stichprobe von 10 Schildkröten einen leicht unterschiedlichen Mittelwert und eine leicht unterschiedliche Standardabweichung aufweist, obwohl sie aus derselben Population stammen:

Stellen wir uns nun vor, dass wir wiederholt Stichproben aus derselben Grundgesamtheit entnehmen und den Stichprobenmittelwert und die Stichprobenstandardabweichung für jede Stichprobe aufzeichnen:

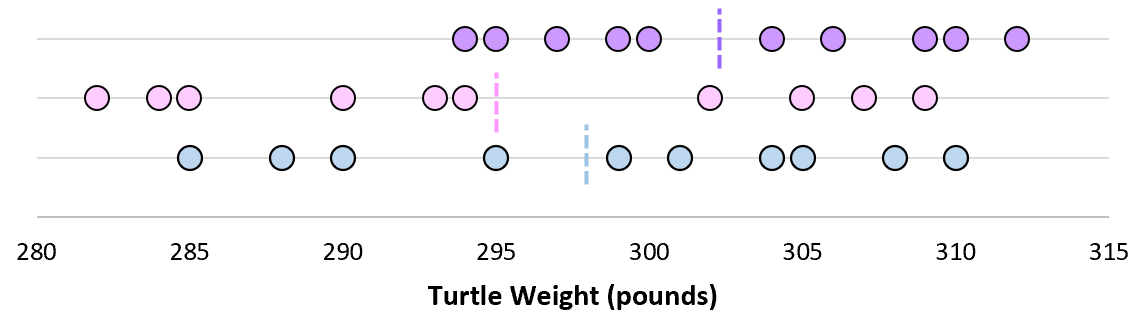
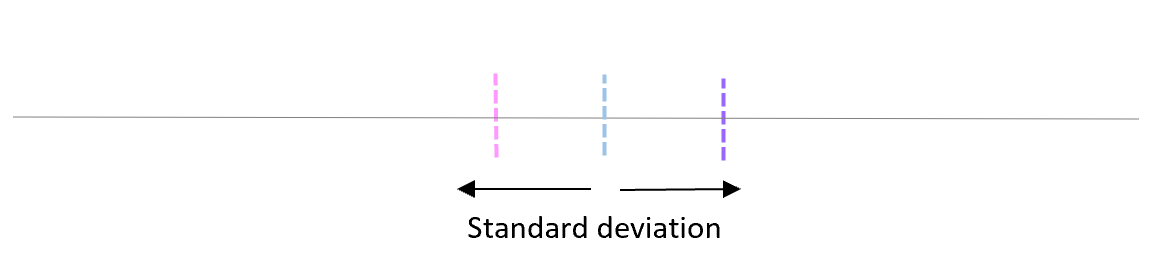
Stellen Sie sich nun vor, dass wir jeden Stichprobenmittelwert auf derselben Linie darstellen:

Die Standardabweichung dieser Mittelwerte wird als Standardfehler bezeichnet.

Die Formel zur tatsächlichen Berechnung des Standardfehlers lautet:

Standardfehler = s/ √ n

Gold:

• s: Stichprobenstandardabweichung
• n: Stichprobengröße

Welchen Sinn hat die Verwendung des Standardfehlers?

Wenn wir den Mittelwert einer bestimmten Stichprobe berechnen, geht es uns eigentlich nicht darum, den Mittelwert dieser bestimmten Stichprobe zu kennen, sondern vielmehr um den Mittelwert der größeren Population, aus der die Stichprobe stammt.

Wir verwenden jedoch Stichproben, da es viel einfacher ist, Daten für sie zu sammeln als für eine gesamte Population.

Und natürlich variiert der Stichprobenmittelwert von Stichprobe zu Stichprobe, daher verwenden wir den Standardfehler des Mittelwerts , um die Präzision unserer Schätzung des Mittelwerts zu messen.

Sie werden in der Formel zur Berechnung des Standardfehlers feststellen, dass mit zunehmender Stichprobengröße (n) der Standardfehler abnimmt:

Standardfehler = s/ √ n

Dies sollte sinnvoll sein, da größere Stichproben die Variabilität verringern und die Wahrscheinlichkeit erhöhen, dass unser Stichprobenmittelwert näher am wahren Bevölkerungsmittelwert liegt.

Wann ist die Standardabweichung gegenüber dem Standardfehler zu verwenden?

Wenn wir lediglich die Verteilung von Werten in einem Datensatz messen möchten, können wir die Standardabweichung verwenden.

Wenn wir jedoch die Unsicherheit rund um eine Schätzung des Mittelwerts quantifizieren möchten, können wir den Standardfehler des Mittelwerts verwenden.

Abhängig von Ihrem spezifischen Szenario und dem, was Sie erreichen möchten, können Sie sich für die Verwendung der Standardabweichung oder des Standardfehlers entscheiden.