So berechnen sie den standardfehler der regression in excel

Wir passen ein lineares Regressionsmodell an. Das Modell hat die folgende Form:

Y = β ₀ + β ₁ X + … + β _i

wobei ϵ ein von X unabhängiger Fehlerterm ist.

Unabhängig davon, wie X verwendet werden kann, um die Werte von Y vorherzusagen, wird es immer zufällige Fehler im Modell geben.

Eine Möglichkeit, die Streuung dieses Zufallsfehlers zu messen, besteht darin, den Standardfehler des Regressionsmodells zu verwenden, mit dem sich die Standardabweichung der Residuen ϵ messen lässt.

Dieses Tutorial bietet ein schrittweises Beispiel für die Berechnung des Standardfehlers eines Regressionsmodells in Excel.

Schritt 1: Erstellen Sie die Daten

Für dieses Beispiel erstellen wir einen Datensatz, der die folgenden Variablen für 12 verschiedene Schüler enthält:

• Prüfungsergebnis
• Stundenlang mit Lernen verbracht
• Aktuelle Klasse

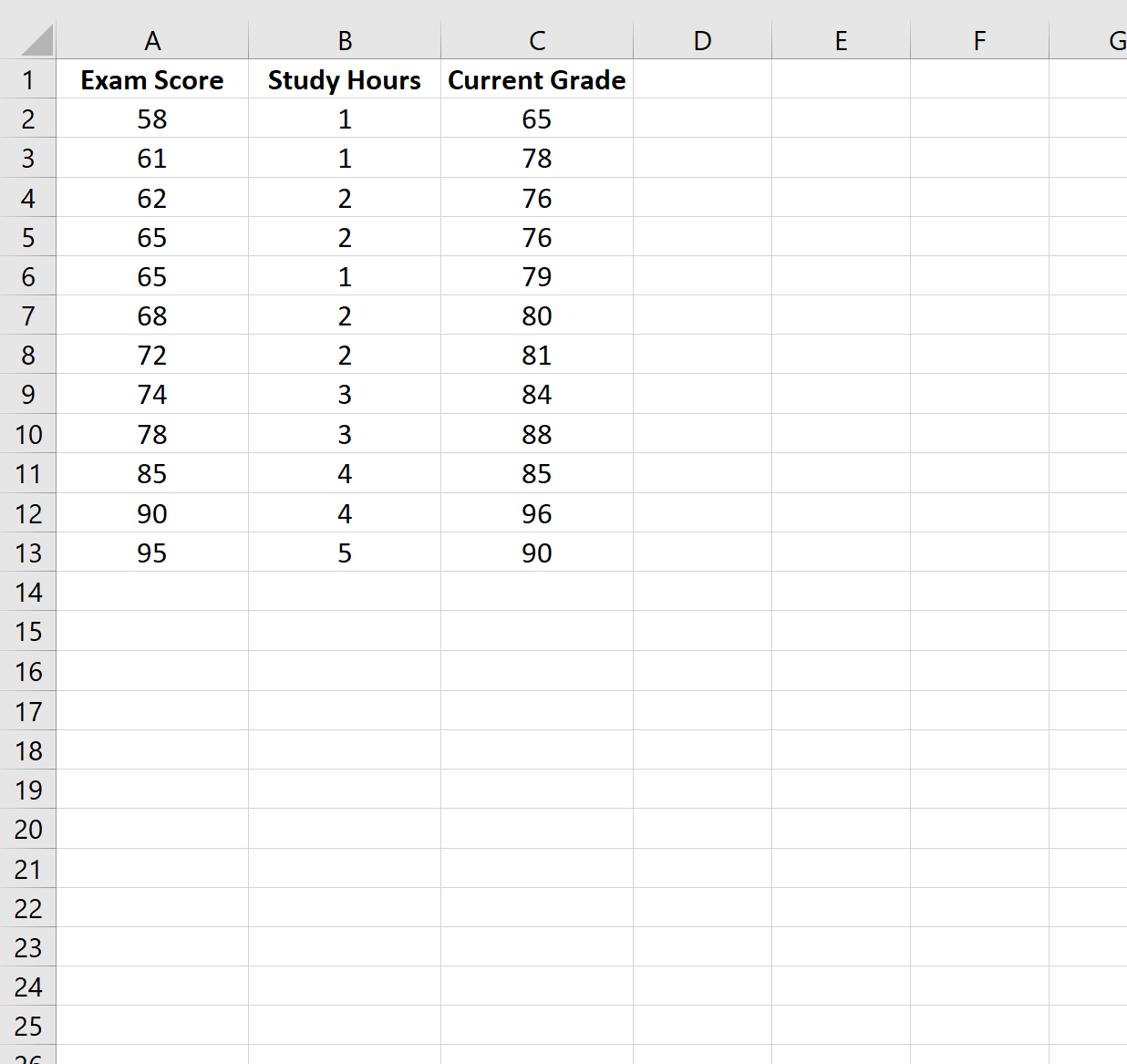
Schritt 2: Passen Sie das Regressionsmodell an

Als Nächstes passen wir ein multiples lineares Regressionsmodell an, wobei wir das Prüfungsergebnis als Antwortvariable und die Lernstunden und die aktuelle Note als Prädiktorvariablen verwenden.

Klicken Sie dazu im oberen Menüband auf die Registerkarte „Daten“ und dann auf „Datenanalyse“ :

Wenn diese Option nicht verfügbar ist, müssen Sie zuerst das Data Analysis ToolPak laden .

Wählen Sie im angezeigten Fenster Regression aus. Geben Sie im neuen Fenster, das erscheint, die folgenden Informationen ein:

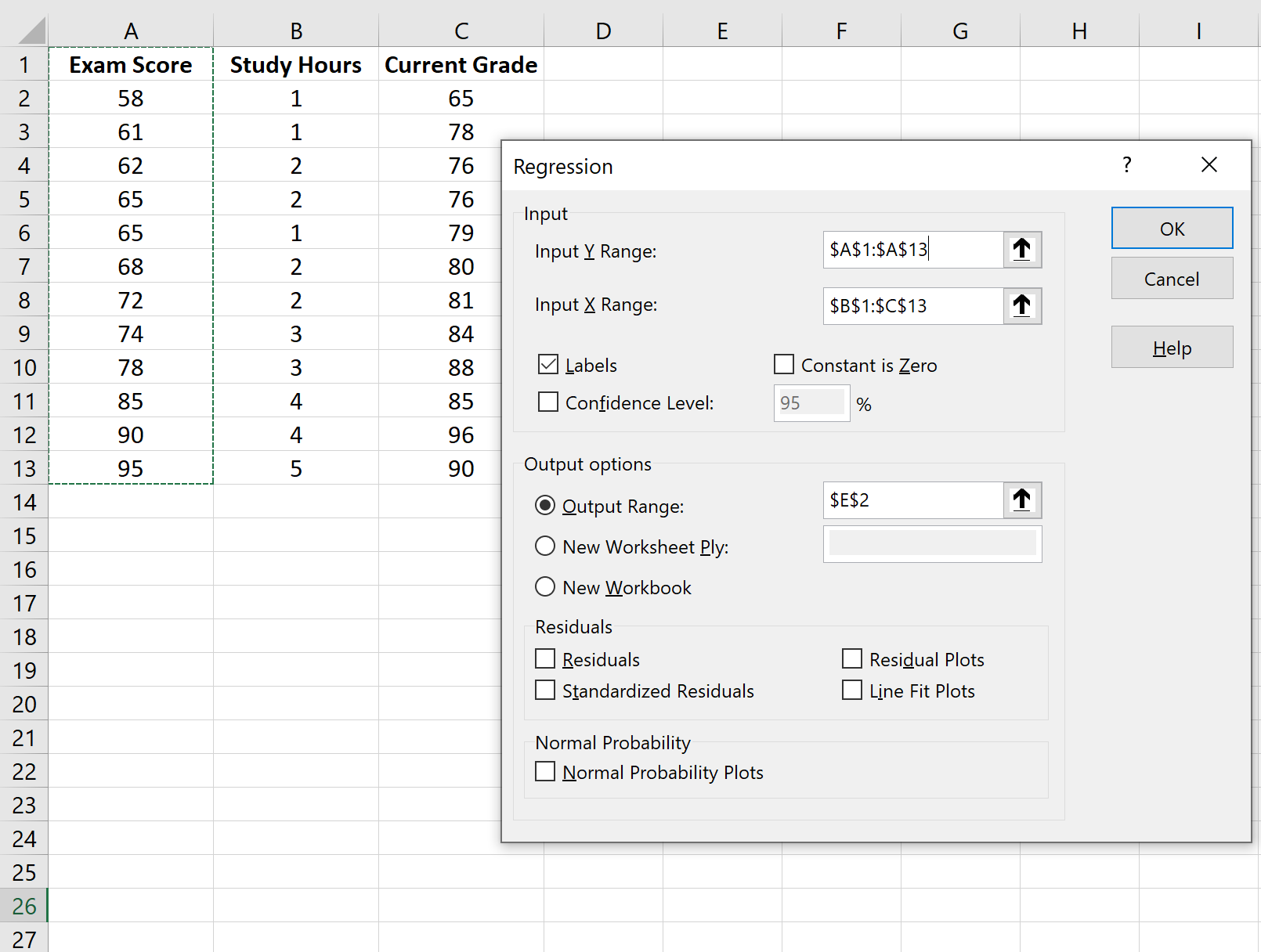
Sobald Sie auf OK klicken, wird die Ausgabe des Regressionsmodells angezeigt:

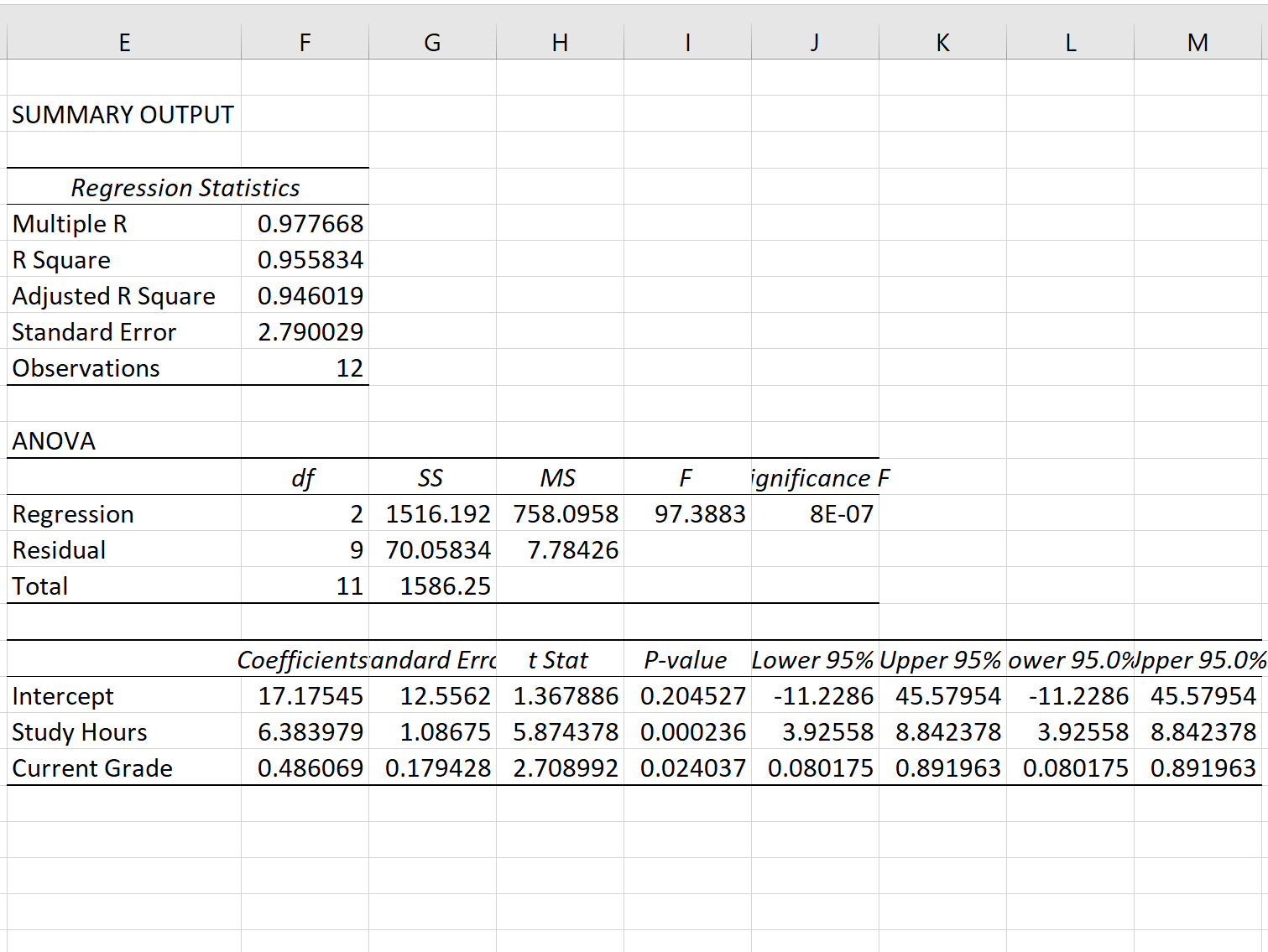
Schritt 3: Interpretieren Sie den Regressionsstandardfehler

Der Standardfehler des Regressionsmodells ist die Zahl neben dem Standardfehler :

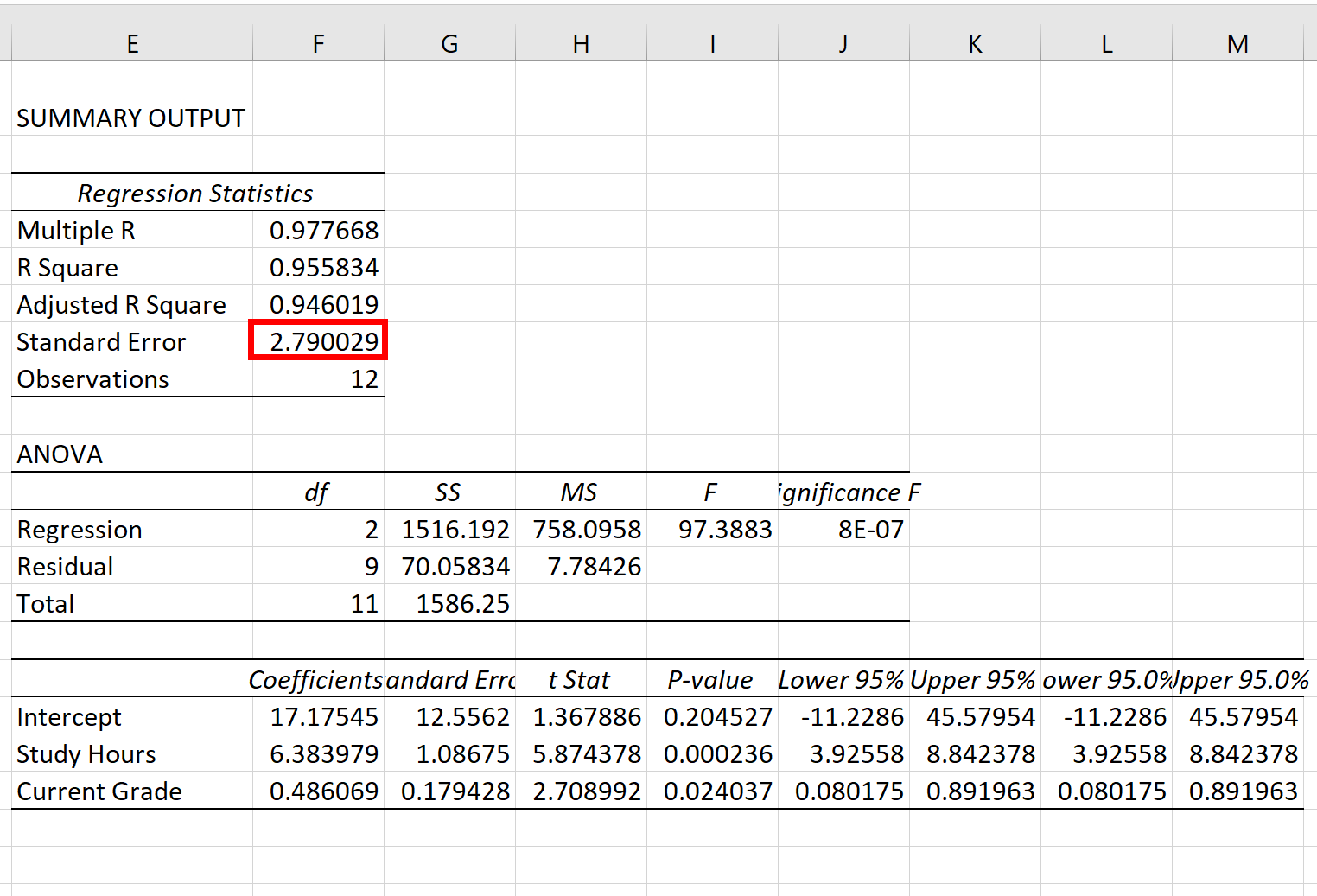
Der Standardfehler dieses speziellen Regressionsmodells beträgt 2,790029 .

Diese Zahl stellt den durchschnittlichen Abstand zwischen den tatsächlichen Prüfungsergebnissen und den vom Modell vorhergesagten Prüfungsergebnissen dar.

Beachten Sie, dass einige Prüfungsergebnisse mehr als 2,79 Einheiten von der vorhergesagten Punktzahl abweichen, während andere näher beieinander liegen. Aber im Durchschnitt beträgt der Abstand zwischen den tatsächlichen Prüfungsergebnissen und den vorhergesagten Ergebnissen 2,790029 .

Beachten Sie außerdem, dass ein kleinerer Standardfehler der Regression darauf hinweist, dass ein Regressionsmodell besser zu einem Datensatz passt.

Wenn wir also ein neues Regressionsmodell an den Datensatz anpassen und einen Standardfehler von beispielsweise 4,53 erhalten, wäre dieses neue Modell bei der Vorhersage von Prüfungsergebnissen weniger effektiv als das vorherige Modell.

Zusätzliche Ressourcen

Eine weitere gängige Methode zur Messung der Genauigkeit eines Regressionsmodells ist die Verwendung des R-Quadrats. In diesem Artikel finden Sie eine schöne Erklärung der Vorteile der Verwendung des Standardfehlers der Regression zur Messung der Genauigkeit im Vergleich zum R-Quadrat.