Den standardfehler einer regressionssteigung verstehen
Der Standardfehler einer Regressionssteigung ist eine Möglichkeit, die „Unsicherheit“ bei der Schätzung einer Regressionssteigung zu messen.
Es wird wie folgt berechnet:
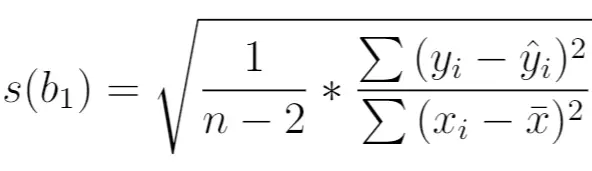
Gold:
- n : Gesamtstichprobengröße
- y i : realer Wert der Antwortvariablen
- ŷ i : vorhergesagter Wert der Antwortvariablen
- x i : realer Wert der Vorhersagevariablen
- x̄ : Durchschnittswert der Vorhersagevariablen
Je kleiner der Standardfehler ist, desto geringer ist die Variabilität um die Koeffizientenschätzung für die Regressionssteigung.
Der Standardfehler der Regressionssteigung wird in der Spalte „Standardfehler“ in der Regressionsausgabe der meisten Statistiksoftware angezeigt:
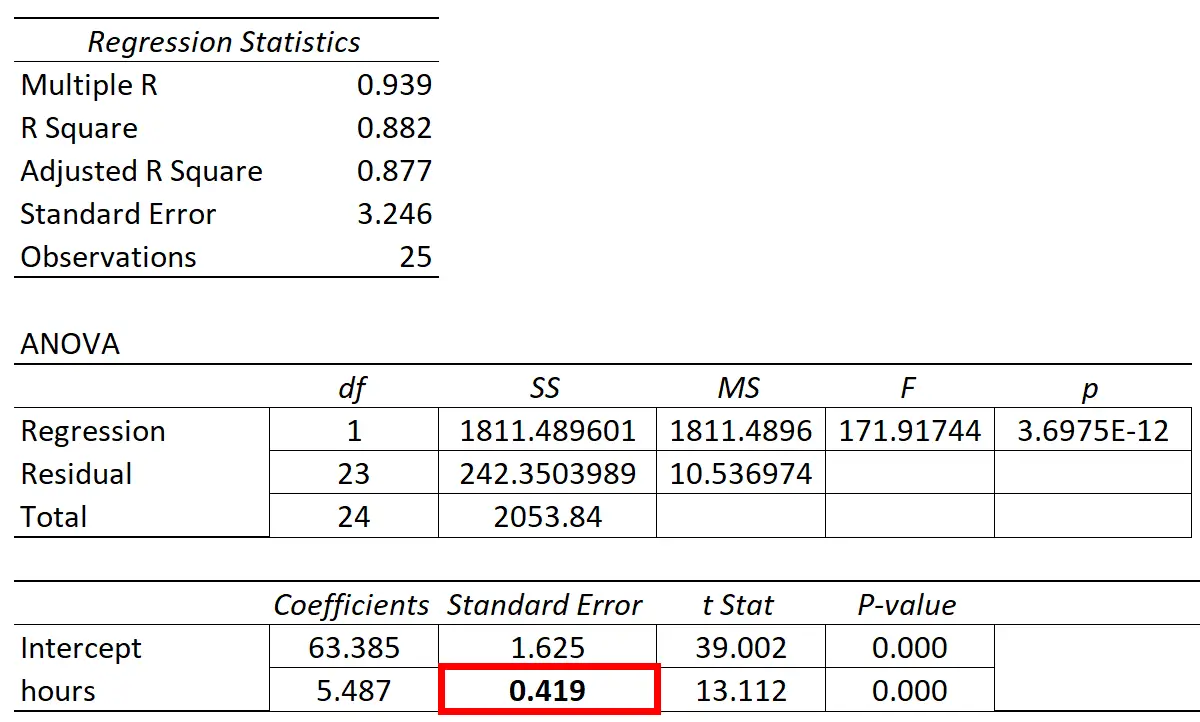
Die folgenden Beispiele zeigen, wie der Standardfehler einer Regressionssteigung in zwei verschiedenen Szenarien interpretiert wird.
Beispiel 1: Interpretation eines kleinen Standardfehlers einer Regressionssteigung
Angenommen, ein Professor möchte den Zusammenhang zwischen der Anzahl der gelernten Stunden und der Abschlussprüfungsnote der Studenten seiner Klasse verstehen.
Es sammelt Daten für 25 Schüler und erstellt das folgende Streudiagramm:
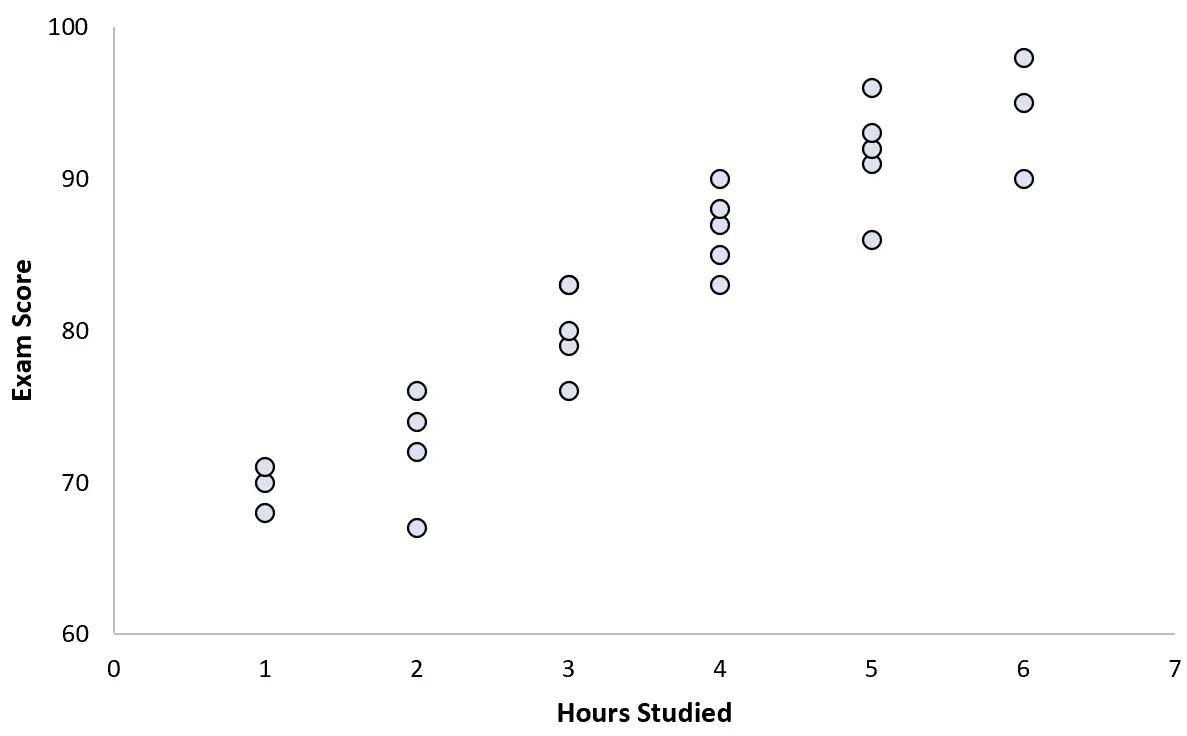
Es besteht ein eindeutig positiver Zusammenhang zwischen den beiden Variablen. Mit zunehmender Anzahl gelernter Stunden erhöht sich die Prüfungspunktzahl in einem ziemlich vorhersehbaren Tempo.
Anschließend passte er ein einfaches lineares Regressionsmodell an, wobei er die untersuchten Stunden als Prädiktorvariable und die Abschlussprüfungsnote als Antwortvariable verwendete.
Die folgende Tabelle zeigt die Regressionsergebnisse:
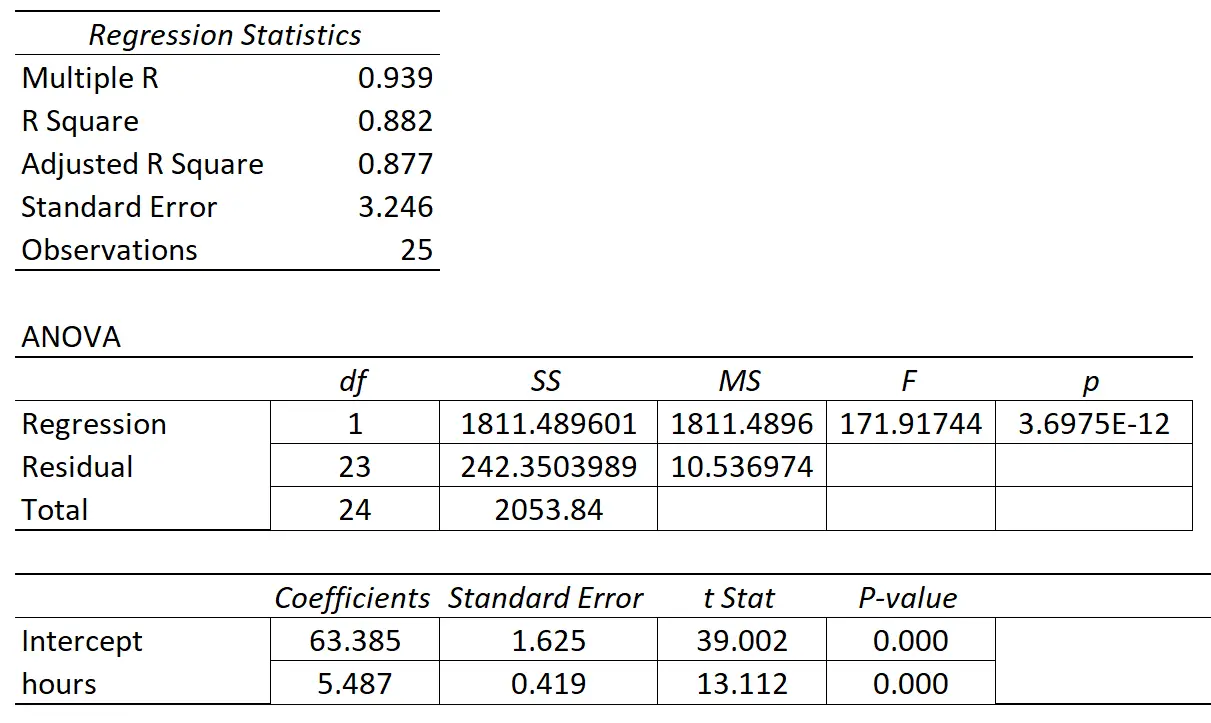
Der Koeffizient der Prädiktorvariablen „Studienstunden“ beträgt 5,487. Dies zeigt uns, dass jede zusätzliche gelernte Stunde mit einer durchschnittlichen Steigerung der Prüfungspunktzahl um 5.487 verbunden ist.
Der Standardfehler beträgt 0,419 und stellt ein Maß für die Variabilität um diese Schätzung für die Regressionssteigung dar.
Mit diesem Wert können wir die t-Statistik für die Prädiktorvariable „Studienstunden“ berechnen:
- t-Statistik = Koeffizientenschätzung / Standardfehler
- t-Statistik = 5,487 / 0,419
- t-Statistik = 13,112
Der p-Wert, der dieser Teststatistik entspricht, beträgt 0,000, was darauf hinweist, dass „gelernte Stunden“ einen statistisch signifikanten Zusammenhang mit der Abschlussnote der Prüfung haben.
Da der Standardfehler der Regressionssteigung im Vergleich zur Koeffizientenschätzung der Regressionssteigung klein war, war die Prädiktorvariable statistisch signifikant.
Beispiel 2: Interpretation eines großen Standardfehlers einer Regressionssteigung
Angenommen, ein anderer Professor möchte den Zusammenhang zwischen der Anzahl der gelernten Stunden und der Abschlussprüfungsnote der Studenten seiner Klasse verstehen.
Sie sammelt Daten für 25 Schüler und erstellt das folgende Streudiagramm:
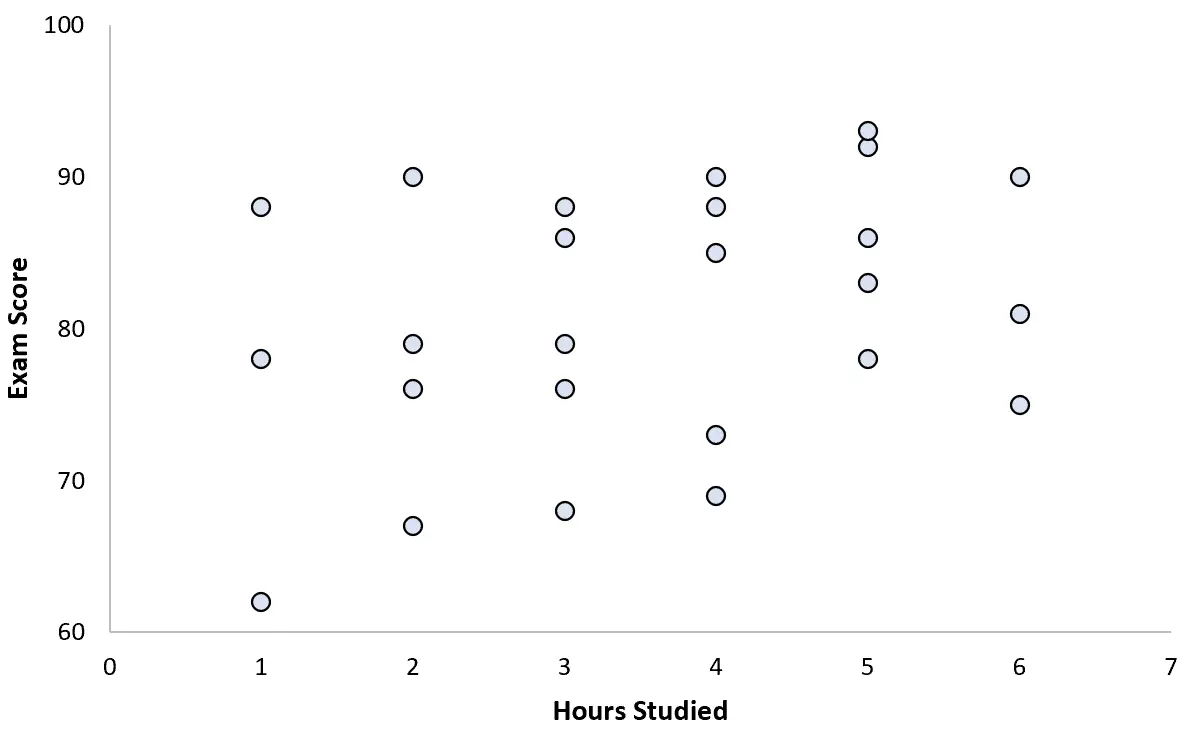
Es scheint ein leicht positiver Zusammenhang zwischen den beiden Variablen zu bestehen. Mit zunehmender Anzahl der Lernstunden erhöht sich im Allgemeinen die Prüfungspunktzahl, jedoch nicht in vorhersehbarem Tempo.
Nehmen wir an, der Professor passt dann ein einfaches lineares Regressionsmodell an, wobei er die untersuchten Stunden als Prädiktorvariable und die Abschlussprüfungsnote als Antwortvariable verwendet.
Die folgende Tabelle zeigt die Regressionsergebnisse:
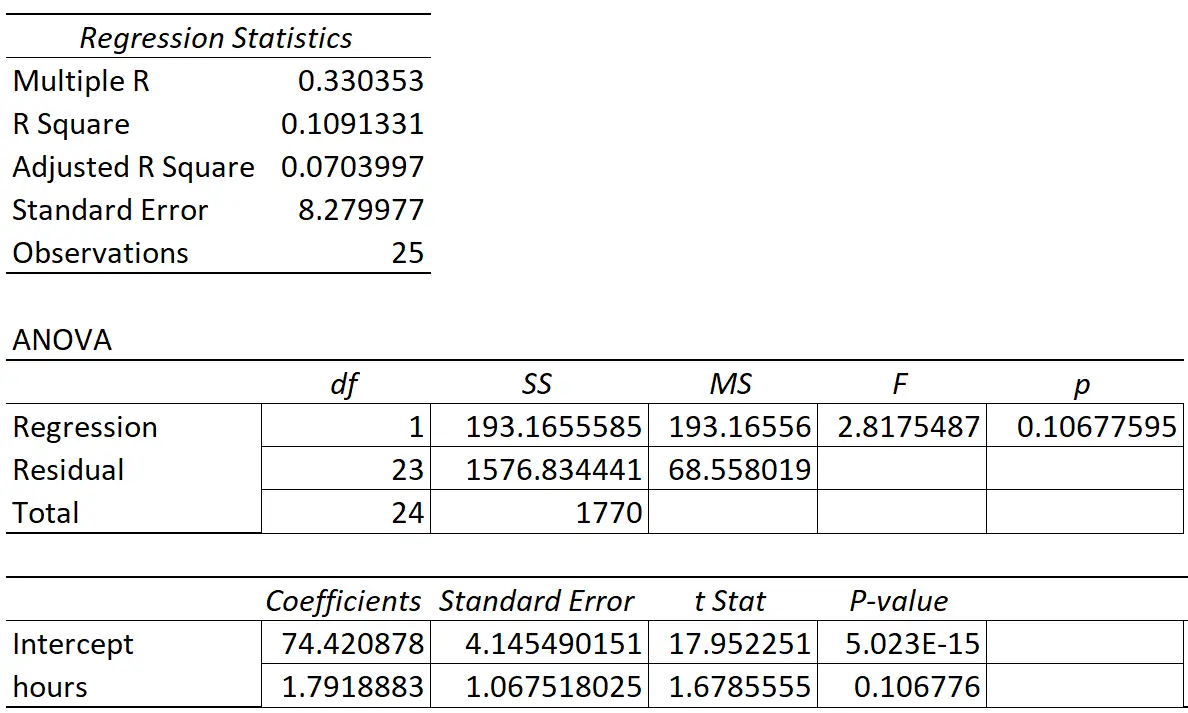
Der Koeffizient der Prädiktorvariablen „Studienstunden“ beträgt 1,7919. Dies zeigt uns, dass jede zusätzliche gelernte Stunde mit einer durchschnittlichen Steigerung der Prüfungspunktzahl um 1,7919 verbunden ist.
Der Standardfehler beträgt 1,0675 und ist ein Maß für die Variabilität um diese Schätzung für die Regressionssteigung.
Mit diesem Wert können wir die t-Statistik für die Prädiktorvariable „Studienstunden“ berechnen:
- t-Statistik = Koeffizientenschätzung / Standardfehler
- t-Statistik = 1,7919 / 1,0675
- t-Statistik = 1,678
Der p-Wert, der dieser Teststatistik entspricht, beträgt 0,107. Da dieser p-Wert nicht weniger als 0,05 beträgt, weist dies darauf hin, dass die Zahl der gelernten Stunden keinen statistisch signifikanten Zusammenhang mit der Note der Abschlussprüfung hat.
Da der Standardfehler der Regressionssteigung im Vergleich zur Koeffizientenschätzung der Regressionssteigung groß war, war die Prädiktorvariable statistisch nicht signifikant.
Zusätzliche Ressourcen
Einführung in die einfache lineare Regression
Einführung in die multiple lineare Regression
So lesen und interpretieren Sie eine Regressionstabelle