Was ist der standardfehler der schätzung? (definition & #038; beispiel)

Der Standardfehler der Schätzung ist eine Möglichkeit, die Genauigkeit der Vorhersagen eines Regressionsmodells zu messen.

Der oft als σ _est bezeichnete Wert wird wie folgt berechnet:

σ _ist = √ Σ(y – ŷ) ² /n

Gold:

• y: Der beobachtete Wert
• ŷ: Der vorhergesagte Wert
• n: Die Gesamtzahl der Beobachtungen

Der Standardfehler der Schätzung gibt uns eine Vorstellung davon, wie gut ein Regressionsmodell zu einem Datensatz passt. Besonders:

• Je kleiner der Wert, desto besser ist die Anpassung.
• Je größer der Wert, desto schlechter ist die Anpassung.

Bei einem Regressionsmodell mit einem kleinen Standardfehler der Schätzung werden die Datenpunkte eng um die geschätzte Regressionslinie gruppiert:

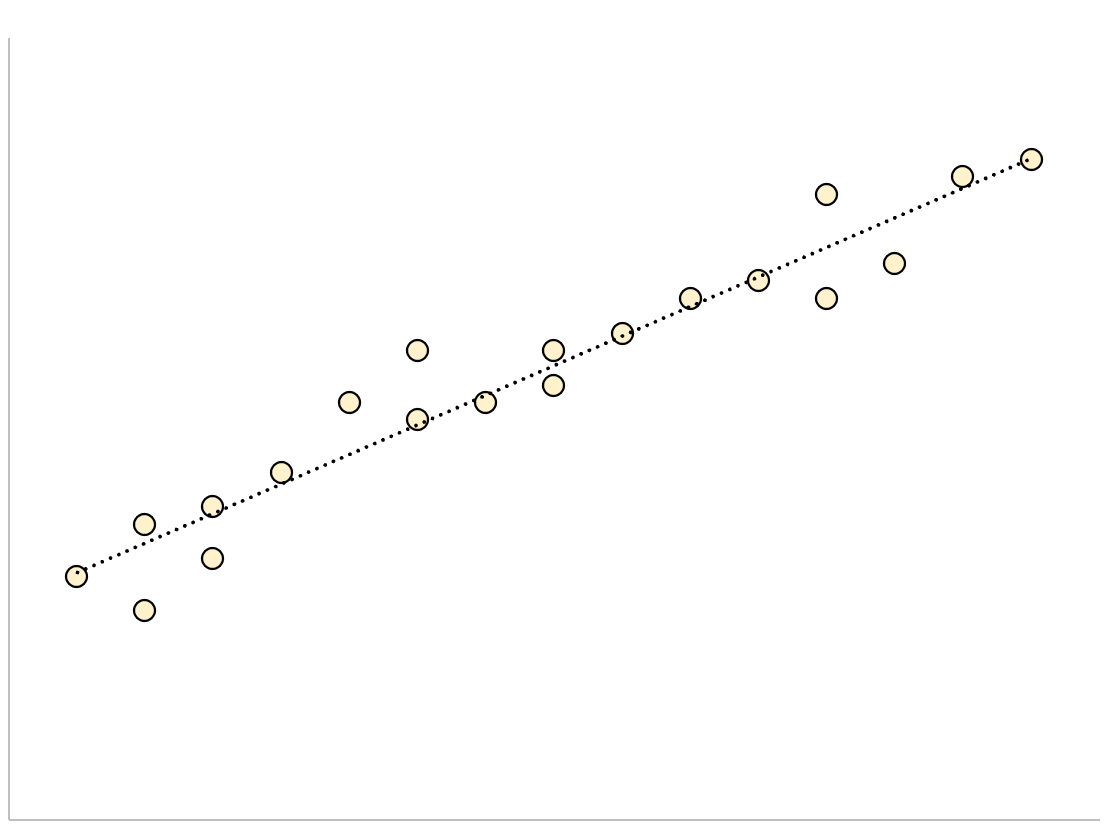
Umgekehrt sind bei einem Regressionsmodell mit einem großen Standardschätzfehler die Datenpunkte lockerer um die Regressionslinie verteilt:

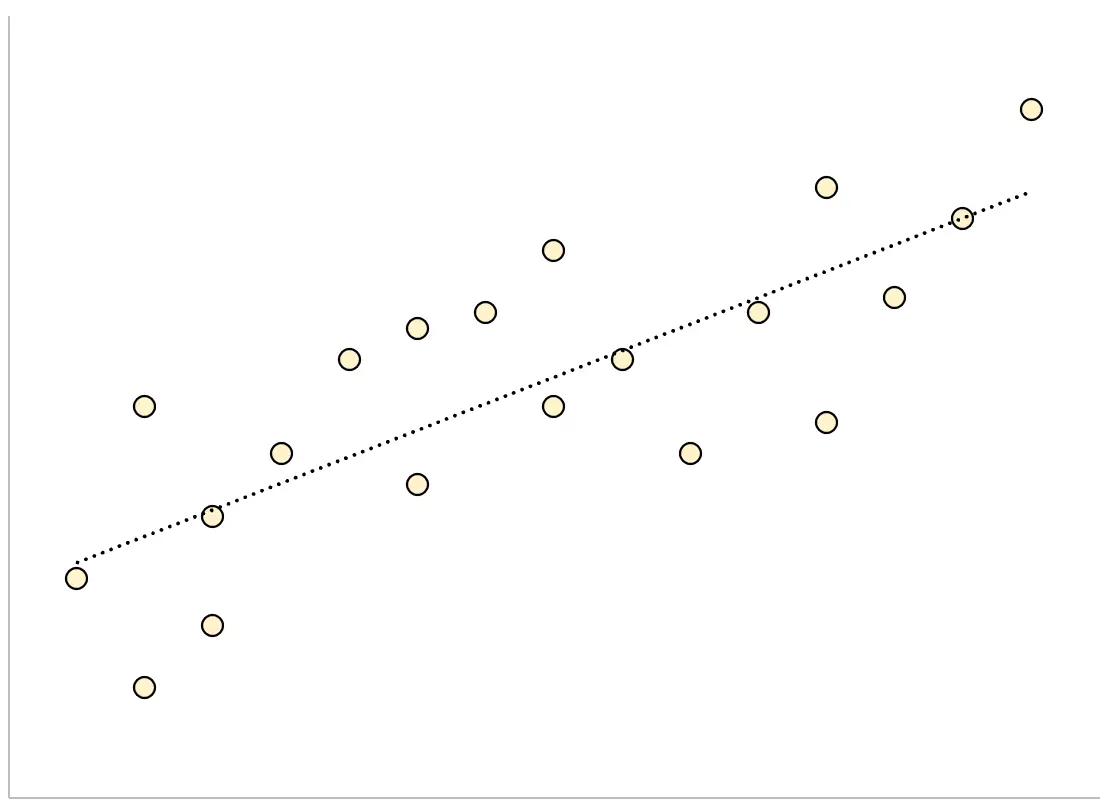
Das folgende Beispiel zeigt, wie der Standardfehler der Schätzung für ein Regressionsmodell in Excel berechnet und interpretiert wird.

Beispiel: Standardfehler der Schätzung in Excel

Führen Sie die folgenden Schritte aus, um den Standardfehler der Schätzung für ein Regressionsmodell in Excel zu berechnen.

Schritt 1: Geben Sie die Daten ein

Geben Sie zunächst die Datensatzwerte ein:

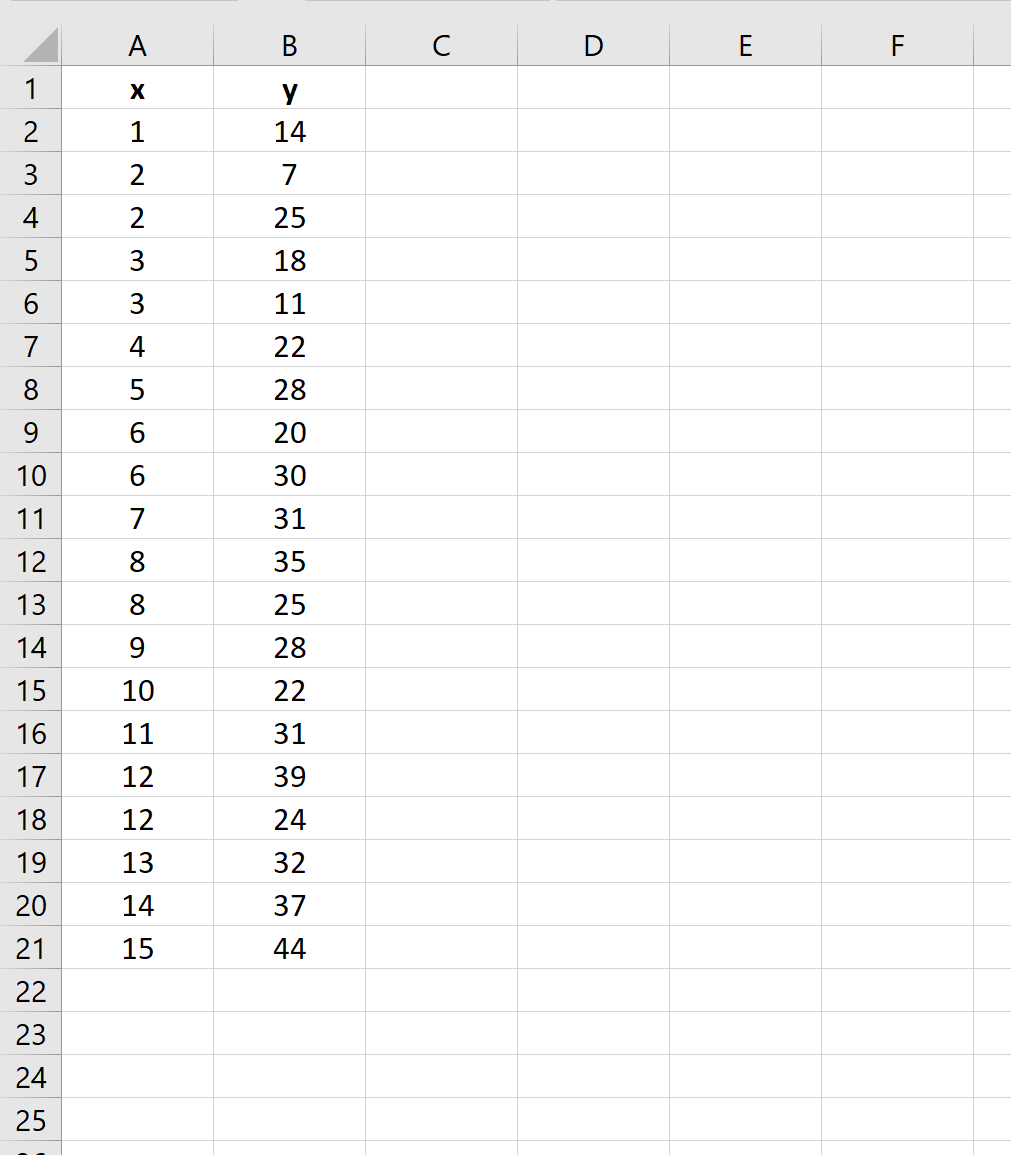
Schritt 2: Führen Sie eine lineare Regression durch

Klicken Sie anschließend im oberen Menüband auf die Registerkarte „Daten“ . Klicken Sie dann in der Gruppe „Analysieren“ auf die Option „Datenanalyse“ .

Wenn diese Option nicht angezeigt wird, müssen Sie zuerst Analysis ToolPak laden .

Klicken Sie im neuen Fenster, das angezeigt wird, auf Regression und dann auf OK .

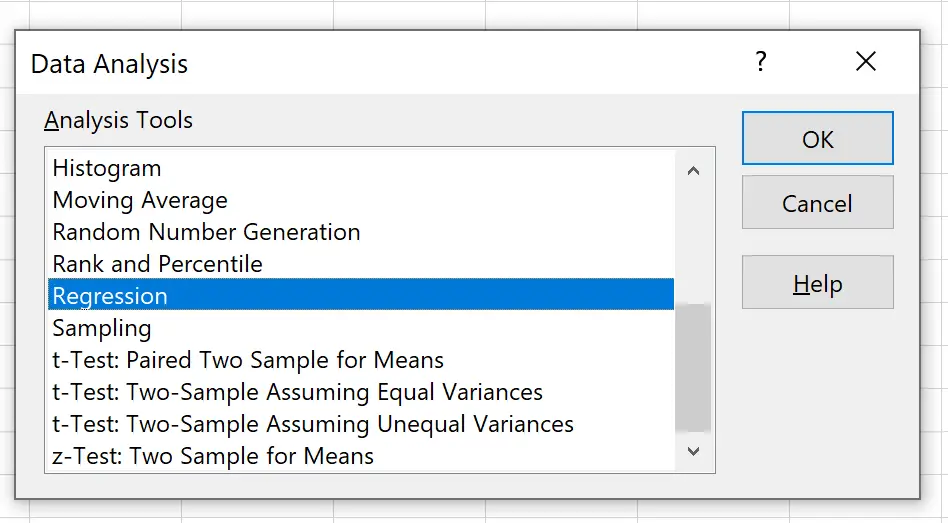
Geben Sie im neuen Fenster, das erscheint, die folgenden Informationen ein:

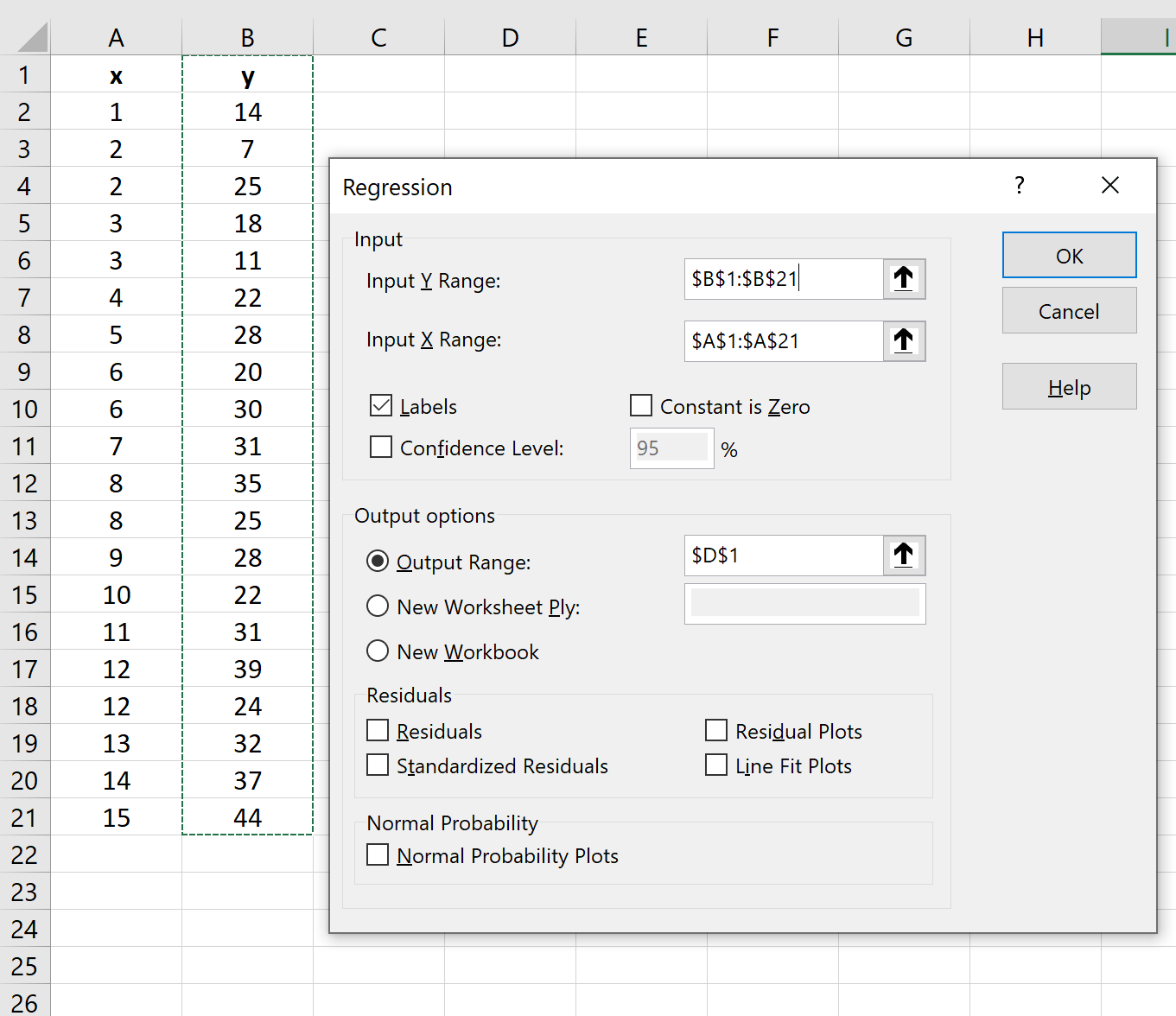
Sobald Sie auf OK klicken, wird das Regressionsergebnis angezeigt:

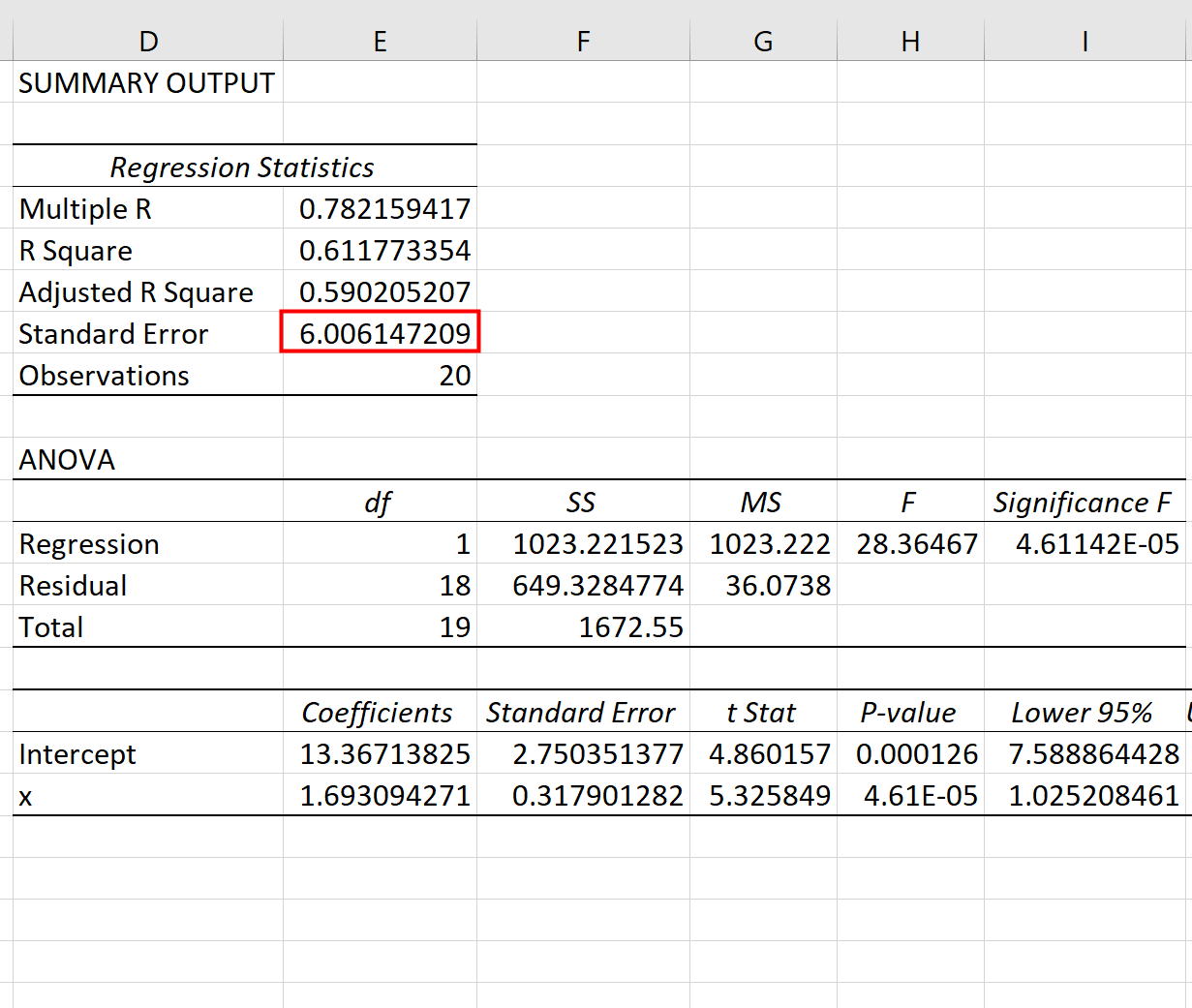
Wir können die Koeffizienten aus der Regressionstabelle verwenden, um die geschätzte Regressionsgleichung zu erstellen:

ŷ = 13,367 + 1,693(x)

Und wir können sehen, dass der Standardfehler der Schätzung für dieses Regressionsmodell 6,006 beträgt. Vereinfacht ausgedrückt bedeutet dies, dass der durchschnittliche Datenpunkt 6,006 Einheiten von der Regressionslinie entfernt ist.

Wir können die geschätzte Regressionsgleichung und den Standardfehler der Schätzung verwenden, um ein 95 %-Konfidenzintervall für den vorhergesagten Wert eines bestimmten Datenpunkts zu erstellen.

Nehmen wir zum Beispiel an, dass x gleich 10 ist. Mithilfe der geschätzten Regressionsgleichung würden wir vorhersagen, dass y gleich wäre:

ŷ = 13,367 + 1,693*(10) = 30,297

Und wir können das 95 %-Konfidenzintervall für diese Schätzung mithilfe der folgenden Formel ermitteln:

• 95 %-KI = [ŷ – 1,96*σ _ist , ŷ + 1,96*σ _ist ]

Für unser Beispiel würde das 95 %-Konfidenzintervall wie folgt berechnet:

• 95 %-KI = [ŷ – 1,96*σ _ist , ŷ + 1,96*σ _ist ]
• 95 % KI = [30,297 – 1,96*6,006, 30,297 + 1,96*6,006]
• 95 %-KI = [18.525, 42.069]

Zusätzliche Ressourcen

So führen Sie eine einfache lineare Regression in Excel durch
So führen Sie eine multiple lineare Regression in Excel durch
So erstellen Sie ein Residuendiagramm in Excel