Was sind standardisierte residuen?

Ein Residuum ist die Differenz zwischen einem beobachteten Wert und einem vorhergesagten Wert in einemRegressionsmodell .

Es wird wie folgt berechnet:

Residuum = Beobachteter Wert – Vorhergesagter Wert

Wenn wir die beobachteten Werte grafisch darstellen und die angepasste Regressionslinie überlagern, wären die Residuen für jede Beobachtung der vertikale Abstand zwischen der Beobachtung und der Regressionslinie:

Eine Art von Residuen, die wir häufig verwenden, um Ausreißer in einem Regressionsmodell zu identifizieren, wird als standardisiertes Residuum bezeichnet.

Es wird wie folgt berechnet:

r _i = e _i / s(e _i ) = e _i / RSE√ 1-h _ii

Gold:

• e _i : Der i- ^te Rest
• RSE: der verbleibende Standardfehler des Modells
• h _ii : Der Aufstieg der ^i-ten Beobachtung

In der Praxis betrachten wir häufig jedes standardisierte Residuum, dessen absoluter Wert größer als 3 ist, als Ausreißer.

Das bedeutet nicht unbedingt, dass wir diese Beobachtungen aus dem Modell entfernen, aber wir sollten sie zumindest weiter untersuchen, um sicherzustellen, dass sie nicht das Ergebnis eines Dateneingabefehlers oder eines anderen seltsamen Ereignisses sind.

Hinweis: Manchmal werden standardisierte Rückstände auch als „intern untersuchte Rückstände“ bezeichnet.

Beispiel: So berechnen Sie standardisierte Residuen

Angenommen, wir haben den folgenden Datensatz mit insgesamt 12 Beobachtungen:

Wenn wir Statistiksoftware (wie R , Excel , Python , Stata usw.) verwenden, um eine lineare Regressionslinie an diesen Datensatz anzupassen, werden wir feststellen, dass die Linie mit der besten Anpassung wie folgt aussieht:

y = 29,63 + 0,7553x

Mithilfe dieser Linie können wir den vorhergesagten Wert für jeden Y-Wert basierend auf dem Wert von X berechnen. Der vorhergesagte Wert der ersten Beobachtung wäre beispielsweise:

y = 29,63 + 0,7553*(8) = 35,67

Wir können dann das Residuum für diese Beobachtung wie folgt berechnen:

Residuum = Beobachteter Wert – Vorhergesagter Wert = 41 – 35,67 = 5,33

Wir können diesen Vorgang wiederholen, um das Residuum für jede Beobachtung zu ermitteln:

Wir können auch statistische Software verwenden, um herauszufinden, dass der verbleibende Standardfehler des Modells 4,44 beträgt.

Und obwohl dies den Rahmen dieses Tutorials sprengen würde, können wir Software verwenden, um die Leverage-Statistik (h _ii ) für jede Beobachtung zu ermitteln:

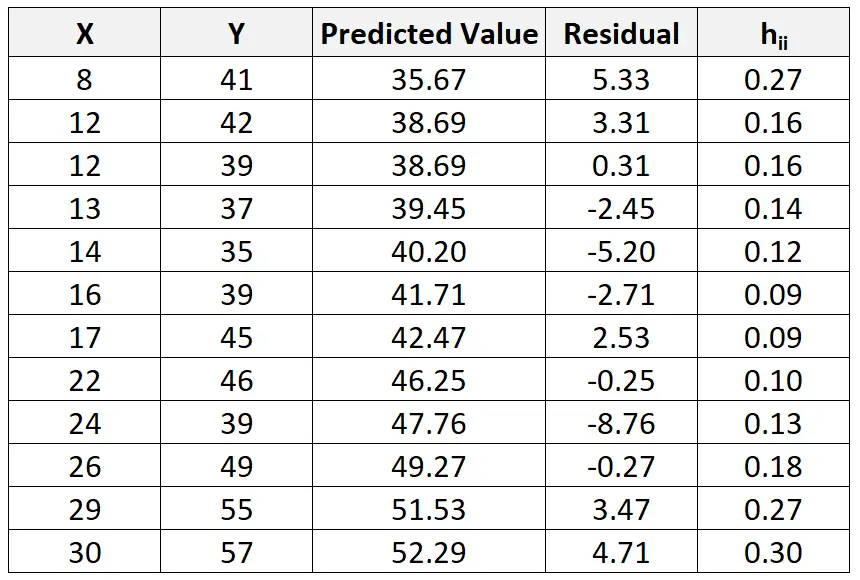
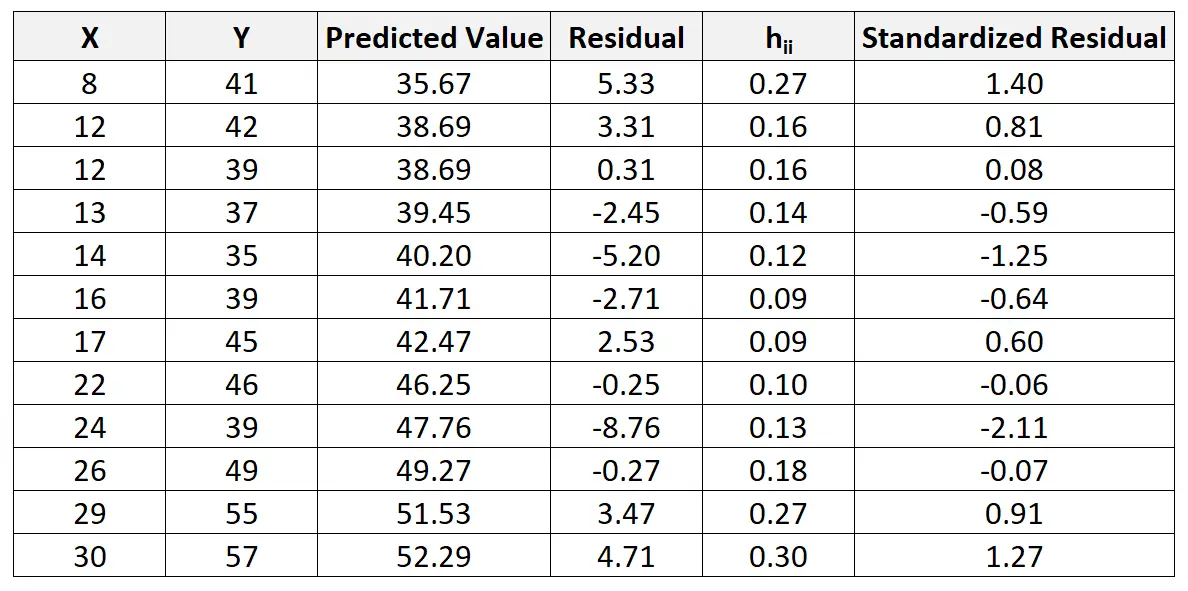
Anschließend können wir die folgende Formel verwenden, um das standardisierte Residuum für jede Beobachtung zu berechnen:

r _i = e _i / RSE√ 1-h _ii

Das standardisierte Residuum für die erste Beobachtung wird beispielsweise wie folgt berechnet:

r _i = 5,33 / 4,44√ 1-0,27 = 1,404

Wir können diesen Vorgang wiederholen, um das standardisierte Residuum für jede Beobachtung zu finden:

Anschließend können wir ein schnelles Streudiagramm der Vorhersagewerte gegenüber den standardisierten Residuen erstellen, um visuell zu sehen, ob einer der standardisierten Residuen einen Absolutwertschwellenwert von 3 überschreitet:

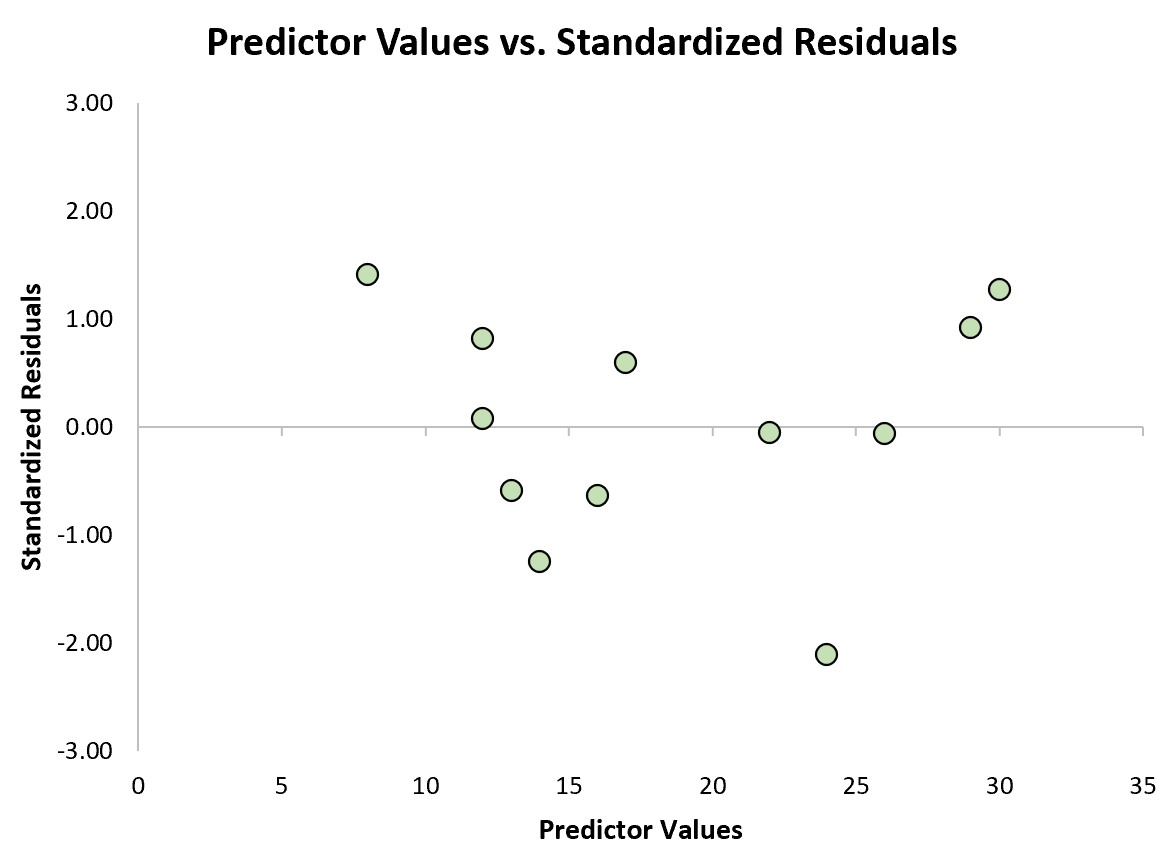
Aus der Grafik können wir ersehen, dass keines der standardisierten Residuen einen absoluten Wert von 3 überschreitet. Somit scheint keine der Beobachtungen Ausreißer zu sein.

Es ist zu beachten, dass Forscher in manchen Fällen Beobachtungen, deren standardisierte Residuen einen absoluten Wert von 2 überschreiten, als Ausreißer betrachten.

Abhängig von dem Fachgebiet, in dem Sie arbeiten, und dem spezifischen Problem, an dem Sie arbeiten, liegt es an Ihnen, ob Sie einen absoluten Wert von 2 oder 3 als Schwellenwert für Ausreißer verwenden möchten.

Zusätzliche Ressourcen

Die folgenden Tutorials bieten zusätzliche Informationen zu standardisierten Residuen:

Was sind Residuen in der Statistik?
So berechnen Sie standardisierte Residuen in Excel
So berechnen Sie standardisierte Residuen in R
So berechnen Sie standardisierte Residuen in Python