Was ist eine standardisierte teststatistik?
Eine statistische Hypothese ist eine Annahme über einen Populationsparameter . Wir können beispielsweise davon ausgehen, dass die durchschnittliche Größe eines Mannes in den Vereinigten Staaten 70 Zoll beträgt. Die Hypothese bezüglich der Körpergröße ist die statistische Hypothese und die wahre Durchschnittsgröße eines Mannes in den Vereinigten Staaten ist der Bevölkerungsparameter .
Ein Hypothesentest ist ein formaler statistischer Test, den wir verwenden, um eine statistische Hypothese abzulehnen oder nicht abzulehnen.
Der grundlegende Prozess zur Durchführung von Hypothesentests ist wie folgt:
1. Sammeln Sie Beispieldaten.
2. Berechnen Sie die standardisierte Teststatistik für die Beispieldaten.
3. Vergleichen Sie die standardisierte Teststatistik mit einem kritischen Wert. Wenn sie extremer als der kritische Wert ist, lehnen Sie die Nullhypothese ab. Andernfalls lehnen Sie den Nullhypothesetest nicht ab.
Die Formel, die wir zur Berechnung der standardisierten Teststatistik verwenden, hängt von der Art des Hypothesentests ab, den wir durchführen.
Die folgende Tabelle zeigt die Formel zur Berechnung der standardisierten Teststatistik für jeden der vier Haupttypen des Hypothesentests:
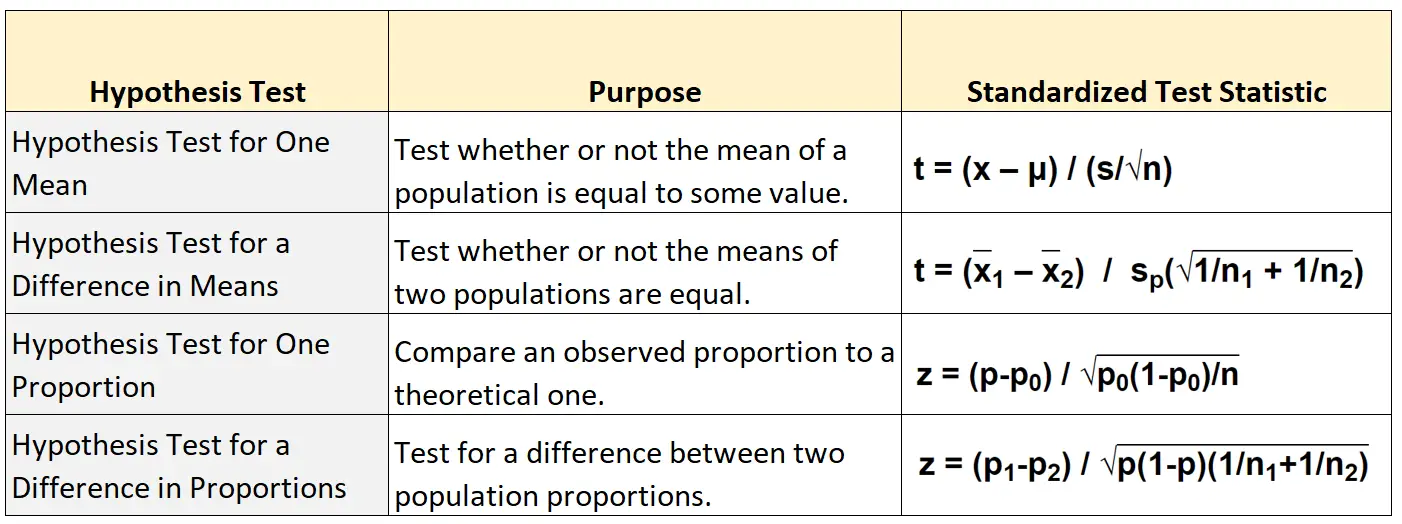
Hypothesentest für einen Durchschnitt
Ein T-Test bei einer Stichprobe wird verwendet, um zu testen, ob der Mittelwert einer Grundgesamtheit einem bestimmten Wert entspricht oder nicht.
Die standardisierte Teststatistik für diese Art von Test wird wie folgt berechnet:
t = ( X – μ) / (s/√n)
Gold:
- x: Stichprobenmittelwert
- μ 0 : hypothetischer Bevölkerungsdurchschnitt
- s: Stichprobenstandardabweichung
- n: Stichprobengröße
In diesem Tutorial finden Sie ein Beispiel für die Berechnung dieser standardisierten Teststatistik.
Hypothesentest auf Mittelwertunterschiede
Ein T-Test mit zwei Stichproben wird verwendet, um zu testen, ob die Mittelwerte zweier Grundgesamtheiten gleich sind oder nicht.
Die standardisierte Teststatistik für diese Art von Test wird wie folgt berechnet:
t = ( X 1 – X 2 ) / s p (√ 1/n 1 + 1/n 2 )
wobei x 1 und x 2 die Stichprobenmittelwerte sind, n 1 und n 2 die Stichprobengrößen sind und wobei sp wie folgt berechnet wird:
s p = √ (n 1 -1)s 1 2 + (n 2 -1)s 2 2 / (n 1 +n 2 -2)
wobei s 1 2 und s 2 2 die Stichprobenvarianzen sind.
In diesem Tutorial finden Sie ein Beispiel für die Berechnung dieser standardisierten Teststatistik.
Hypothesentest für einen Anteil
Ein One-Proportion-Z-Test wird verwendet, um einen beobachteten Anteil mit einem theoretischen Anteil zu vergleichen.
Die standardisierte Teststatistik für diese Art von Test wird wie folgt berechnet:
z = (pp 0 ) / √ p 0 (1-p 0 )/n
Gold:
- p: beobachteter Probenanteil
- p 0 : hypothetischer Anteil der Bevölkerung
- n: Stichprobengröße
In diesem Tutorial finden Sie ein Beispiel für die Berechnung dieser standardisierten Teststatistik.
Hypothesentest für einen Unterschied in den Proportionen
Ein Zwei-Proportionen-Z-Test wird verwendet, um einen Unterschied zwischen zwei Bevölkerungsanteilen zu testen.
Die standardisierte Teststatistik für diese Art von Test wird wie folgt berechnet:
z = (p 1 -p 2 ) / √ p(1-p)(1/n 1 +1/n 2 )
Dabei sind p 1 und p 2 die Stichprobenanteile, n 1 und n 2 die Stichprobengrößen und p der gesamte gepoolte Anteil, der wie folgt berechnet wird:
p = (p 1 n 1 + p 2 n 2 )/(n 1 + n 2 )
In diesem Tutorial finden Sie ein Beispiel für die Berechnung dieser standardisierten Teststatistik.
Über den Autor
Dr. Benjamin Anderson
Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen