Standardisierung oder normalisierung: was ist der unterschied?

Standardisierung und Normalisierung sind zwei Möglichkeiten, die Größe von Daten zu ändern.

Durch die Normalisierung wird ein Datensatz so skaliert, dass er einen Mittelwert von 0 und eine Standardabweichung von 1 aufweist. Dazu wird die folgende Formel verwendet:

x _neu = (x _i – x ) / s

Gold:

• x _i : der ^i-te Wert des Datensatzes
• x : Das Stichprobenmittel
• s : die Standardabweichung der Stichprobe

Durch die Normalisierung wird die Größe eines Datensatzes so geändert, dass jeder Wert zwischen 0 und 1 liegt. Dies geschieht mithilfe der folgenden Formel:

x _neu = (x _i – x _min ) / (x _max – x _min )

Gold:

• x _i : der ^i-te Wert des Datensatzes
• x _min : Der Mindestwert im Datensatz
• x _max : Der Maximalwert im Datensatz

Die folgenden Beispiele zeigen, wie man einen Datensatz in der Praxis standardisiert und normalisiert.

Beispiel: So standardisieren Sie Daten

Angenommen, wir haben den folgenden Datensatz:

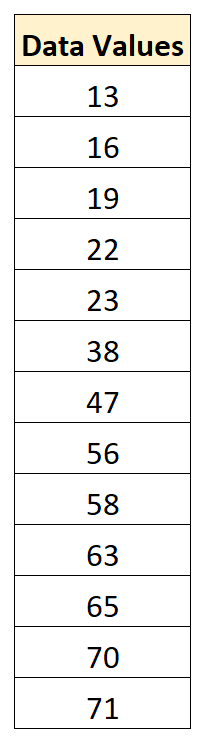
Der Durchschnittswert im Datensatz beträgt 43,15 und die Standardabweichung beträgt 22,13.

Um den ersten Wert von 13 zu normalisieren, würden wir die zuvor geteilte Formel anwenden:

• x _neu = (x _i – x ) / s = (13 – 43,15) / 22,13 = -1,36

Um den zweiten Wert von 16 zu normalisieren, würden wir dieselbe Formel verwenden:

• x _neu = (x _i – x ) / s = (16 – 43,15) / 22,13 = -1,23

Um den dritten Wert von 19 zu normalisieren, würden wir dieselbe Formel verwenden:

• x _neu = (x _i – x ) / s = (19 – 43,15) / 22,13 = -1,09

Wir können genau dieselbe Formel verwenden, um jeden Wert im Originaldatensatz zu standardisieren:

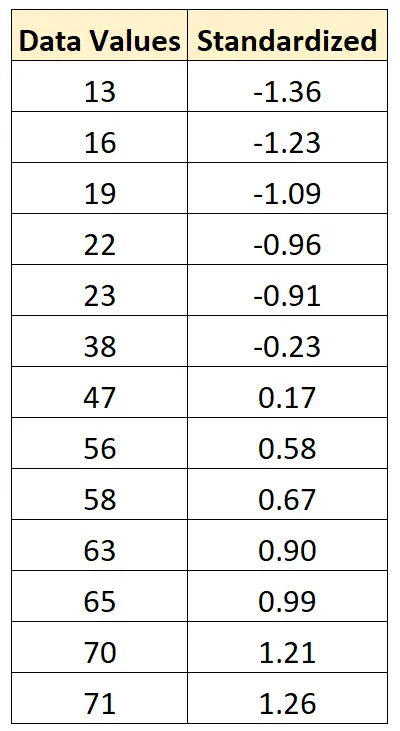
Beispiel: So normalisieren Sie Daten

Nehmen wir erneut an, dass wir den folgenden Datensatz haben:

Der Mindestwert im Datensatz beträgt 13 und der Höchstwert 71.

Um den ersten Wert von 13 zu normalisieren, würden wir die zuvor geteilte Formel anwenden:

• x _neu = (x _i – x _min ) / (x _max – x _min ) = (13 – 13) / (71 – 13) = 0

Um den zweiten Wert von 16 zu normalisieren, würden wir dieselbe Formel verwenden:

• x _neu = (x _i – x _min ) / (x _max – x _min ) = (16 – 13) / (71 – 13) = 0,0517

Um den dritten Wert von 19 zu normalisieren, würden wir dieselbe Formel verwenden:

• x _neu = (x _i – x _min ) / (x _max – x _min ) = (19 – 13) / (71 – 13) = 0,1034

Wir können genau dieselbe Formel verwenden, um jeden Wert im Originaldatensatz zwischen 0 und 1 zu normalisieren:

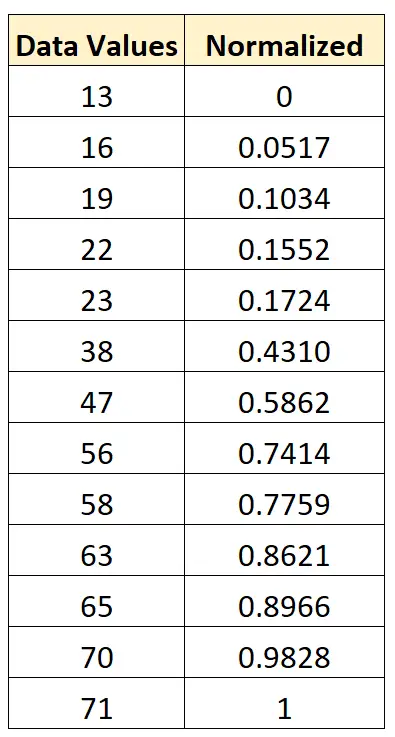
Standardisierung oder Normalisierung: Wann sollten sie verwendet werden?

Typischerweise normalisieren wir Daten, wenn wir eine Art Analyse durchführen, bei der wir mehrere Variablen in unterschiedlichen Maßstäben messen und möchten, dass jede der Variablen denselben Bereich hat.

Dies verhindert, dass eine Variable einen unzulässigen Einfluss hat, insbesondere wenn sie in unterschiedlichen Einheiten gemessen wird (z. B. wenn eine Variable in Zoll und eine andere in Yards gemessen wird).

Andererseits normalisieren wir Daten normalerweise, wenn wir wissen möchten, wie viele Standardabweichungen jeder Wert in einem Datensatz vom Mittelwert hat.

Beispielsweise verfügen wir möglicherweise über eine Liste der Prüfungsergebnisse von 500 Schülern einer bestimmten Schule und möchten wissen, um wie viele Standardabweichungen jedes Prüfungsergebnis vom Durchschnittsergebnis abweicht.

In diesem Fall könnten wir die Rohdaten normalisieren, um diese Informationen zu kennen. Dann würde uns eine standardisierte Punktzahl von 1,26 sagen, dass die Prüfungspunktzahl dieses bestimmten Schülers 1,26 Standardabweichungen über der durchschnittlichen Prüfungspunktzahl liegt.

Unabhängig davon, ob Sie sich für die Normalisierung oder Standardisierung Ihrer Daten entscheiden, beachten Sie die folgenden Punkte:

• Ein normalisierter Datensatz wird immer Werte zwischen 0 und 1 haben.
• Ein standardisierter Datensatz hat einen Mittelwert von 0 und eine Standardabweichung von 1, es gibt jedoch keine spezifische Ober- oder Untergrenze für die Maximal- und Minimalwerte.

Abhängig von Ihrem speziellen Szenario kann es sinnvoller sein, die Daten zu normalisieren oder zu standardisieren.

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie Sie Daten in verschiedenen Statistikprogrammen standardisieren und normalisieren:

So normalisieren Sie Daten in R
So normalisieren Sie Daten in Excel
So normalisieren Sie Daten in Python
So standardisieren Sie Daten in R