So interpretieren sie ein maßstabs- und standortdiagramm: mit beispielen

Ein skaliertes Standortdiagramm ist eine Art Diagramm, das die angepassten Werte eines Regressionsmodells entlang der x-Achse und die Quadratwurzel der standardisierten Residuen entlang der y-Achse anzeigt.

Wenn wir uns diese Grafik ansehen, überprüfen wir zwei Dinge:

1. Stellen Sie sicher, dass die rote Linie im Diagramm ungefähr horizontal verläuft. Wenn dies der Fall ist, ist die Annahme der Homoskedastizität für ein bestimmtes Regressionsmodell wahrscheinlich erfüllt. Das heißt, die Verteilung der Residuen ist für alle angepassten Werte ungefähr gleich.

2. Stellen Sie sicher, dass es keinen klaren Trend zwischen den Residuen gibt. Mit anderen Worten: Die Residuen sollten zufällig um die rote Linie verteilt sein und für alle angepassten Werte ungefähr die gleiche Variabilität aufweisen.

Maßstabs- und Standortdarstellung in R

Wir können den folgenden Code verwenden, um ein einfaches lineares Regressionsmodell in R anzupassen und ein Maßstabs- und Standortdiagramm für das resultierende Modell zu erstellen:

 #fit simple linear regression model
model <- lm(Ozone ~ Temp, data = airquality)

#produce scale-location plot
plot(model)

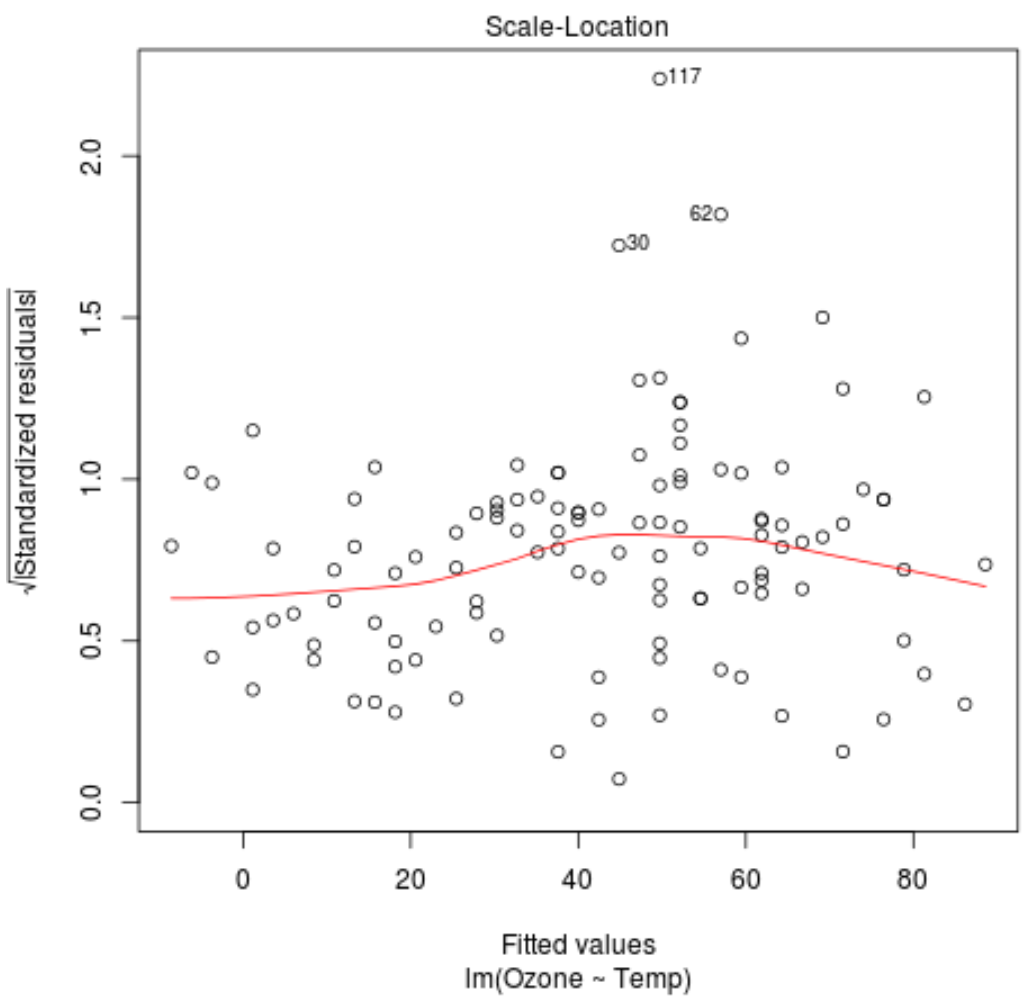
Aus dem Skalen-Ort-Diagramm dieses Regressionsmodells können wir die folgenden zwei Dinge beobachten.

1. Die rote Linie verläuft im Diagramm ungefähr horizontal. Wenn dies der Fall ist, dann ist die Annahme der Homoskedastizität für ein gegebenes Regressionsmodell erfüllt. Das heißt, die Verteilung der Residuen ist für alle angepassten Werte ungefähr gleich.

2. Stellen Sie sicher, dass es keinen klaren Trend zwischen den Residuen gibt. Mit anderen Worten: Die Residuen sollten zufällig um die rote Linie verteilt sein und für alle angepassten Werte ungefähr die gleiche Variabilität aufweisen.

Technische Hinweise

Die drei Beobachtungen aus dem Datensatz mit den höchsten standardisierten Residuen sind in der Grafik gekennzeichnet.

Wir können sehen, dass die Beobachtungen in den Zeilen 30, 62 und 117 die höchsten standardisierten Residuen aufweisen.

Dies bedeutet nicht zwangsläufig, dass es sich bei diesen Beobachtungen um Ausreißer handelt. Möglicherweise möchten Sie sich jedoch die Originaldaten ansehen, um diese Beobachtungen genauer zu untersuchen.

Obwohl wir sehen können, dass die rote Linie im Skalenstandortdiagramm ungefähr horizontal verläuft, dient dies nur als visuelle Möglichkeit, um zu sehen, ob die Annahme der Homoskedastizität erfüllt ist.

Ein formaler statistischer Test, mit dem wir prüfen können, ob die Annahme der Homoskedastizität erfüllt ist, ist derBreusch-Pagan-Test .

Breusch-Pagan-Test in R

Der folgende Code zeigt, wie Sie die Funktion bptest() des Pakets lmtest verwenden, um einen Breusch-Pagan-Test in R durchzuführen:

 #load lmtest package
library(lmtest)

#perform Breusch-Pagan Test
bptest(model)

	studentized Breusch-Pagan test

data: model
BP = 1.4798, df = 1, p-value = 0.2238

Ein Breusch-Pagan-Test verwendet die folgenden Null- und Alternativhypothesen:

• Nullhypothese (H ₀ ): Die Residuen sind homoskedastisch (d. h. gleichmäßig verteilt)
• Alternativhypothese ( _HA ): Die Residuen sind heteroskedastisch (d. h. nicht gleichmäßig verteilt)

Aus dem Ergebnis können wir ersehen, dass der p-Wert des Tests 0,2238 beträgt. Da dieser p-Wert nicht kleiner als 0,05 ist, können wir die Nullhypothese nicht ablehnen. Wir haben keine ausreichenden Beweise, um zu behaupten, dass Heteroskedastizität im Regressionsmodell vorhanden ist.

Dieses Ergebnis stimmt mit unserer visuellen Inspektion der roten Linie im Maßstab-Standort-Diagramm überein.

Zusätzliche Ressourcen

Heteroskedastizität in der Regressionsanalyse verstehen
So erstellen Sie ein Residuendiagramm in R
So führen Sie einen Breusch-Pagan-Test in R durch