Mode (statistik)
In diesem Artikel wird erläutert, um welchen Modus es sich in der Statistik handelt. Sie erfahren, wie Sie den Statistikmodus für gruppierte und nicht gruppierte Daten finden, welche verschiedenen Modustypen es gibt und wie Sie mehrere Beispiele für dieses statistische Maß finden.
Was ist der Modus in der Statistik?
In der Statistik ist der Modus der Wert im Datensatz, der die höchste absolute Häufigkeit aufweist, d. h. der Modus ist der am häufigsten wiederholte Wert in einem Datensatz.
Um den Modus eines statistischen Datensatzes zu berechnen, zählen Sie daher einfach, wie oft jedes Datenelement in der Stichprobe vorkommt. Die am häufigsten wiederholten Daten ergeben den Modus.
Der Modus wird zum Definieren einer statistischen Verteilung verwendet, da der am häufigsten wiederholte Wert normalerweise in der Mitte der Verteilung liegt.
Der Modus kann auch als statistischer Modus oder Modalwert bezeichnet werden. Wenn Daten in Intervalle gruppiert werden, ist das am häufigsten wiederholte Intervall das Modalintervall oder die Modalklasse .
Im Allgemeinen wird der Begriff Mo als Symbol für den statistischen Modus verwendet, beispielsweise ist der Verteilungsmodus X Mo(X).
Bedenken Sie, dass der Modus ein statistisches Maß für die Mittelposition sowie für Median und Mittelwert ist. Im Folgenden werden wir sehen, was jedes dieser statistischen Maße bedeutet.
Modustypen in der Statistik
In der Statistik gibt es verschiedene Arten von Modi, die nach der Anzahl der am häufigsten wiederholten Werte klassifiziert werden:
- Unimodaler Modus : Es gibt nur einen Wert mit der maximalen Anzahl an Wiederholungen. Zum Beispiel [1, 4, 2, 4, 5, 3].
- Bimodaler Modus : Die maximale Anzahl an Wiederholungen erfolgt bei zwei unterschiedlichen Werten, und beide Werte werden gleich oft wiederholt. Zum Beispiel [2, 6, 7, 2, 3, 6, 9].
- Multimodaler Modus : Drei oder mehr Werte haben die gleiche maximale Wiederholungszahl. Zum Beispiel [3, 3, 4, 1, 3, 4, 2, 1, 4, 5, 2, 1].
So finden Sie den Statistikmodus
Um den statistischen Modus eines Datensatzes zu ermitteln, müssen Sie die folgenden Schritte ausführen:
- Ordnen Sie die Daten. Dieser Schritt ist nicht zwingend erforderlich, erleichtert aber das Zählen von Zahlen.
- Zählen Sie, wie oft jede Zahl vorkommt.
- Die Zahl, die am häufigsten erscheint, ist der Statistikmodus.
Beispiele für den Statistikmodus
In Anbetracht der Definition von Mode in der Statistik sehen Sie unten ein Beispiel für jede Art von Mode, damit Sie das Konzept besser verstehen können.
Beispiel für einen unimodalen Modus
- Welchen Modus hat der folgende Datensatz?
![]()
Die Nummern sind nicht geordnet, daher werden wir sie zuerst ordnen, um das Auffinden des Modus zu erleichtern.
![]()
Die Zahlen 2 und 9 erscheinen zweimal, aber die Zahl 5 wird dreimal wiederholt. Daher ist der Modus der Datenreihe Nummer 5.
![]()
Beispiel für einen bimodalen Modus
- Berechnen Sie den Modus des folgenden Datensatzes:
![]()
![]()
Zuerst bringen wir die Zahlen in die richtige Reihenfolge:
![]()
![]()
Wie Sie sehen, kommen die Zahl 6 und die Zahl 8 insgesamt viermal vor, was der maximalen Wiederholungszahl entspricht. Daher handelt es sich in diesem Fall um einen bimodalen Modus und die beiden Zahlen sind der Modus des Datensatzes:
![]()
Beispiel für einen multimodalen Modus
- Suchen Sie den folgenden Datensatzmodus:
![]()
![]()
![]()
Da es viele Daten gibt, sortieren wir sie zunächst in aufsteigender Reihenfolge, um das Zählen zu erleichtern:
![]()
![]()
![]()
Die am häufigsten wiederholten Zahlen sind 20, 27 und 31, alle drei Zahlen werden fünfmal wiederholt. Der Modus dieses Beispiels ist daher multimodal.
![]()
Moderechner
Geben Sie Daten aus einer beliebigen statistischen Stichprobe in den folgenden Online-Rechner ein, um deren Modus zu berechnen. Die Daten müssen durch ein Leerzeichen getrennt und mit dem Punkt als Dezimaltrennzeichen eingegeben werden.
Modus für gruppierte Daten
Wenn wir Daten in Form von Intervallen gruppiert haben, wissen wir nicht wirklich, wie oft jedes Datenelement wiederholt wird, wir kennen nur die Häufigkeit jedes Intervalls.
Um den Modus der in Intervallen gruppierten Daten zu berechnen, müssen wir daher die folgende Formel verwenden :
![]()
Gold:
- L i ist die untere Grenze des Modalintervalls (höchstes absolutes Frequenzintervall).
- f i ist die absolute Häufigkeit des Modalintervalls.
- f i-1 ist die absolute Häufigkeit des Intervalls vor dem Modal.
- f i+1 ist die absolute Häufigkeit des Intervalls nach dem Modal.
- A i ist die Breite des Modalintervalls.
Als Beispiel haben Sie unten eine Übung gelöst, in der der Modus der in Intervallen gruppierten Daten berechnet wird:
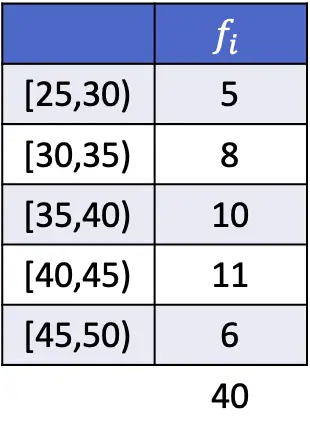
In diesem Fall beträgt das Modalintervall [40,45), da es das Intervall mit der größten absoluten Häufigkeit ist. Daher sind die Parameter der Modusformel für gruppierte Daten:
![Rendered by QuickLaTeX.com \begin{array}{c}L_i=40\\[2ex]f_i=11\\[2ex]f_{i-1}=10\\[2ex]f_{i+1}=6\\[2ex]A_i=5\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-85aef7092d3e0c7769ad17b96aae294c_l3.png)
Wir wenden daher die Formel an, um den Modus der in Intervallen gruppierten Daten zu bestimmen, und führen die Berechnung durch:
![Rendered by QuickLaTeX.com \begin{aligned}Mo & =L_i+ \cfrac{f_i-f_{i-1}}{(f_i-f_{i-1})+(f_i-f_{i+1})}\cdot A_i\\[2ex]& =40+ \cfrac{11-10}{(11-10)+(11-6)}\cdot 5\\[2ex]&=40,83\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-3ee33fdb43267fdcfc6d222ed6798fca_l3.png)
Unterschied zwischen Modus, Mittelwert und Median
In diesem letzten Abschnitt werden wir sehen, was der Unterschied zwischen dem Modus, dem Mittelwert und dem Median ist. Da es sich bei allen dreien um statistische Maße der zentralen Position handelt, ist ihre Bedeutung unterschiedlich.
Wie im gesamten Artikel erläutert, ist der Modus in der Mathematik der am häufigsten wiederholte Wert in einem Datensatz.
Zweitens ist der Mittelwert der Durchschnittswert aller statistischen Daten. Um den Durchschnitt bestimmter Daten zu erhalten, müssen Sie daher alle Daten addieren und dann das Ergebnis durch die Anzahl der Beobachtungen dividieren.
Und schließlich ist der Median der Wert, der bei der Sortierung der Daten die zentrale Position einnimmt.
Somit helfen die drei statistischen Maße dabei, eine Wahrscheinlichkeitsverteilung zu definieren, da sie eine Vorstellung von ihren zentralen Werten liefern. Bedenken Sie jedoch, dass es keine Maßnahme gibt, die besser ist als die andere, es handelt sich lediglich um unterschiedliche Konzepte.
Modeimmobilien
Die Modeeigenschaften sind:
- Der Modus kann sowohl in quantitativen als auch in qualitativen Variablen gefunden werden.
- Wenn wir eine lineare Transformation auf eine Zufallsvariable anwenden, ändert sich der Mittelwert abhängig von den angewendeten Operationen.
- Im Allgemeinen ist der Modus unempfindlich gegenüber Ausreißern.
- Wenn alle Werte die gleiche Häufigkeit haben, gibt es keinen Modus.
![]()