Socs: ein nützliches akronym zur beschreibung von verteilungen

In der Statistik wollen wir oft verstehen, wie ein Datensatz verteilt ist. Es gibt insbesondere vier Dinge, die man über eine Distribution wissen sollte:

1 . Form

• Ist die Verteilung symmetrisch oder einseitig schief?
• Ist die Verteilung unimodal (ein Peak) oder bimodal (zwei Peaks)?

2. Ausreißer

• Sind in der Verteilung Ausreißer vorhanden?

3. Mitte

• Was ist Mittelwert, Median und Verteilungsart?

4.Verteilen

• Was sind Bereich, Interquartilbereich, Standardabweichung und Varianz der Verteilung?

SOCS ist ein nützliches Akronym, mit dem wir uns an diese vier Dinge erinnern können. Es bedeutet „Form, Ausreißer, Zentrum, Ausbreitung“.

Lassen Sie uns ein einfaches Beispiel für die Verwendung von SOCS zur Beschreibung einer Verteilung durchgehen.

Beispiel: So verwenden Sie SOCS zur Beschreibung einer Verteilung

Nehmen wir an, wir haben den folgenden Datensatz, der die Höhe einer Stichprobe von 20 verschiedenen Pflanzen zeigt.

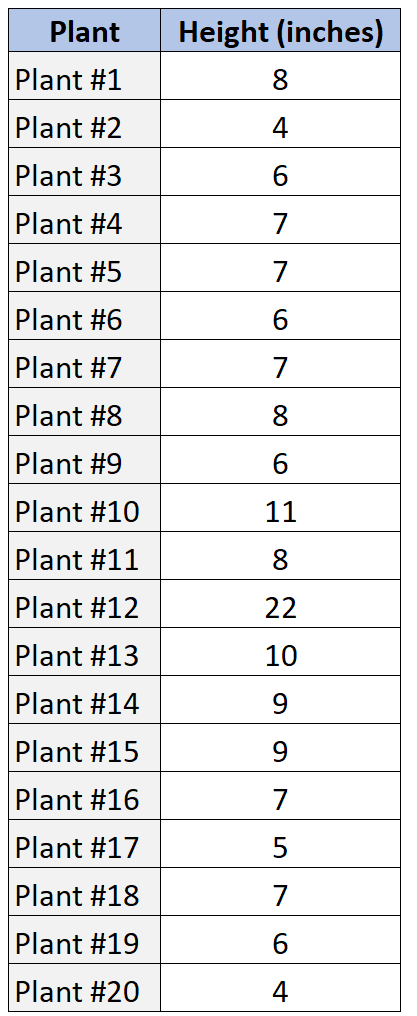
So können wir SOCS verwenden, um diese Verteilung von Datenwerten zu beschreiben.

Form

Zunächst wollen wir die Form der Verteilung beschreiben.

Eine nützliche Möglichkeit, die Form der Verteilung zu visualisieren, besteht darin, ein Histogramm zu erstellen, das die Häufigkeiten jedes Werts im Datensatz anzeigt:

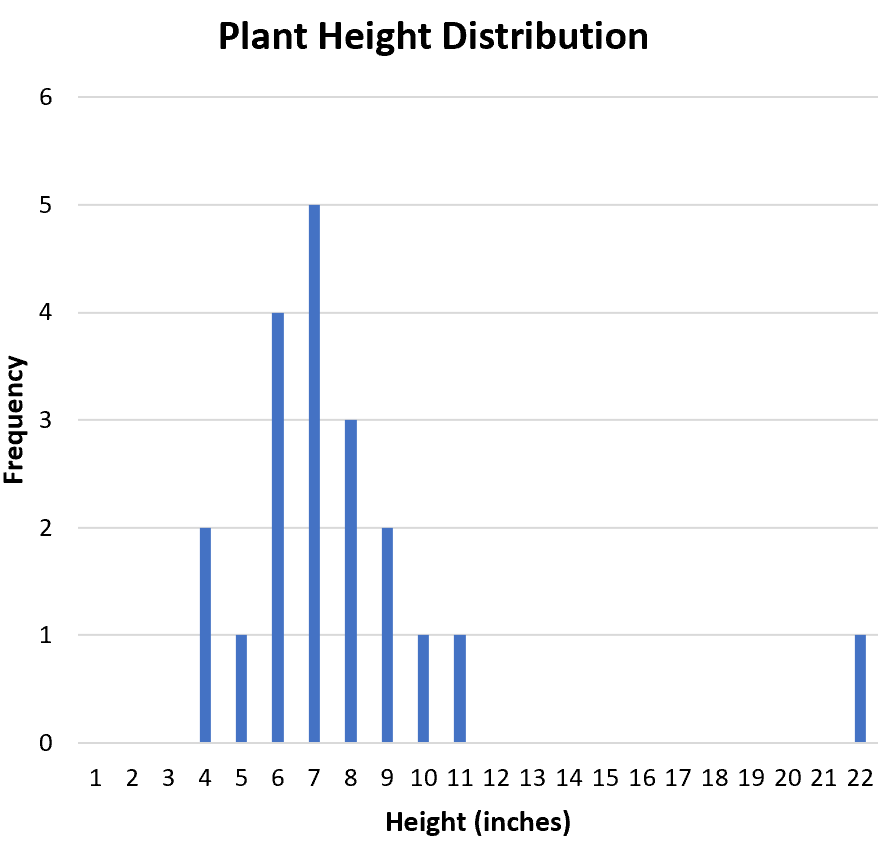
Ist die Verteilung symmetrisch oder einseitig schief?   Aus dem Histogramm können wir erkennen, dass die Verteilung annähernd symmetrisch ist. Mit anderen Worten: Die Werte sind weder in die eine noch in die andere Richtung verzerrt.

Ist die Verteilung unimodal (ein Peak) oder bimodal (zwei Peaks)? Die Verteilung ist unimodal. Es hat einen Höhepunkt beim Wert „7“.

Ausreißer

Als nächstes möchten wir feststellen, ob der Datensatz Ausreißer enthält. Anhand des Histogramms können wir die Verteilung visuell überprüfen und erkennen, dass 22 möglicherweise ein Ausreißer ist:

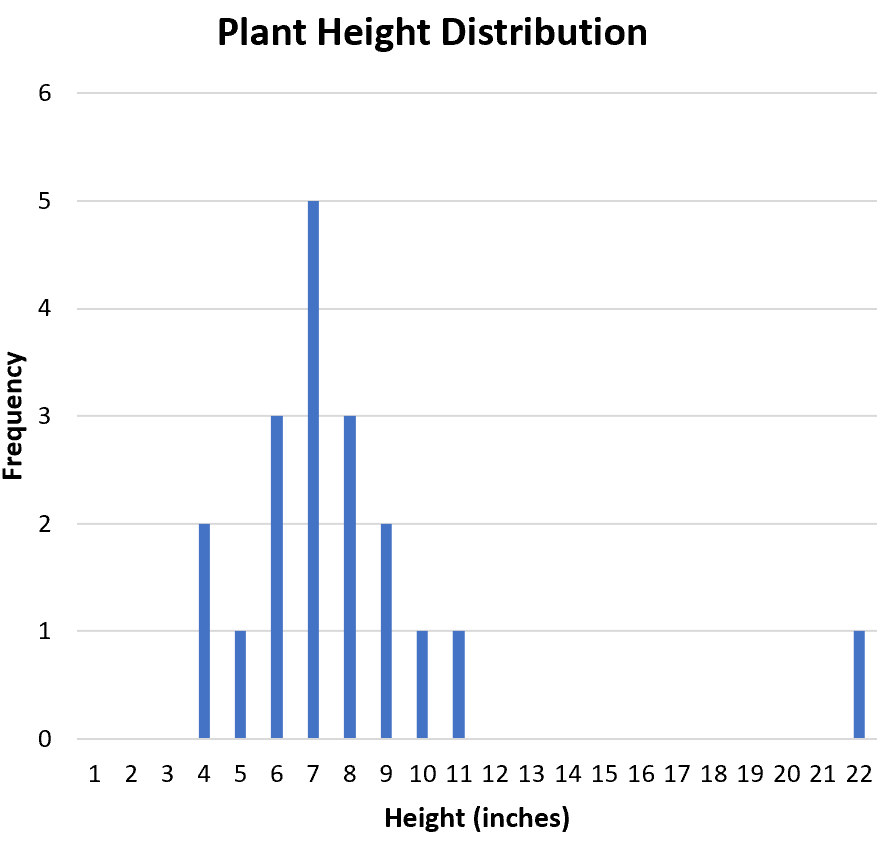
Eine gängige Methode zur formalen Definition eines Ausreißers ist jeder Wert, der das 1,5-fache des Interquartilbereichs über dem dritten Quartil oder unter dem ersten Quartil beträgt.

Mit dem Interquartilbereichsrechner können wir die 20 Rohdatenwerte eingeben und sehen, dass das dritte Quartil 9 ist, der Interquartilbereich 3 ist und daher jeder Wert größer als 9 + (1,5*3) = 13,5 ein Ausreißer ist. per Definition.

Da 22 größer als 13,5 ist, können wir 22 als Ausreißer deklarieren.

Center

Anschließend wollen wir beschreiben, wo das Zentrum der Verteilung liegt. Drei gängige Maßeinheiten für die zentrale Tendenz , die wir verwenden können, sind Mittelwert, Median und Modus.

Mittelwert: Dies ist der Durchschnittswert der Verteilung. Das finden wir, indem wir alle Einzelwerte addieren und dann durch die Gesamtzahl der Werte dividieren:

Durchschnitt = (8+4+6+7+7+6+7+8+6+11+8+22+10+9+9+7+5+7+6+4) / 20 = 7,85

Median: Dies ist der „durchschnittliche“ Wert der Verteilung. Wir finden dies, indem wir alle Werte vom kleinsten zum größten ordnen und dann den Medianwert ermitteln. Es stellt sich heraus, dass es 7 ist.

4, 4, 5, 6, 6, 6, 6, 7, 7, 7, 7 , 7, 8 , 8, 8, 9, 9, 10, 11, 22

Modus: Dies ist der Wert, der am häufigsten erscheint. Es stellt sich heraus, dass es 7 ist.

Verbreiten

Als nächstes wollen wir die Verteilung der Werte in der Verteilung beschreiben. Vier gängige Streuungsmaße, die wir verwenden können, sind Reichweite, Interquarilbereich, Standardabweichung und Varianz.

Bereich: Dies ist die Differenz zwischen dem größten und kleinsten Wert im Datensatz. Das ergibt 22 – 4 = 18 .

Interquartilbereich: Misst die Breite der mittleren 50 % der Datenwerte. Wenn wir die 20 Rohdatenwerte in den Interquartilbereichsrechner eingeben, können wir sehen, dass dies gleich 3 ist.

Standardabweichung: Dies ist ein Maß für die durchschnittliche Verteilung von Datenwerten. Wenn wir die 20 Rohdatenwerte in den Varianz- und Standardabweichungsrechner eingeben, können wir sehen, dass die Standardabweichung 3,69 beträgt.

Varianz: Dies ist einfach die quadratische Standardabweichung. Dies entspricht 3,69 ² = 13,63 .

Abschluss

Mithilfe von SOCS konnten wir die Pflanzenhöhenverteilung wie folgt beschreiben:

• Die Verteilung war unimodal und symmetrisch, das heißt, sie hatte nur einen Peak und war weder zur einen noch zur anderen Seite verzerrt.
• Die Verteilung hatte einen Ausreißer: 22.
• Die Verteilung hatte einen Mittelwert von 7,85, einen Median von 7 und einen Modus von 7.
• Die Verteilung hatte einen Bereich von 18, einen Interquartilbereich von 3, eine Standardabweichung von 3,69 und eine Varianz von 13,63.

Beachten Sie, dass wir SOCS verwenden können, um jede Verteilung zu beschreiben. Dies ist eine nützliche Möglichkeit für uns, die Form einer Verteilung vollständig zu verstehen, ob sie Ausreißer hat, wo sich ungefähr der Mittelpunkt befindet und wie die Datenwerte verteilt werden. Sind.