Statistische formeln

Von Dr. Benjamin Anderson August 1, 2023 Statistiken Keine Kommentare

Hier finden Sie die wichtigsten statistischen Formeln. Wir hinterlassen Ihnen auch Links zu unseren Artikeln, in denen Sie Anwendungsbeispiele für jede statistische Formel sehen können. Darüber hinaus können Sie einen Online-Rechner verwenden, um die Berechnungen nicht durchführen zu müssen und das Ergebnis der Formel direkt zu erfahren.

Formeln für statistische Maße der zentralen Tendenz

Halb

Um den Durchschnitt zu berechnen, addieren Sie alle Werte und teilen Sie sie dann durch die Gesamtzahl der Daten. Die Formel für den Durchschnitt lautet daher wie folgt:

$\displaystyle\overline{x}=\frac{\displaystyle\sum_{i=1}^n x_i}{n}$

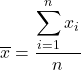
In der Statistik wird der Mittelwert auch als arithmetisches Mittel oder Durchschnitt bezeichnet.

➤ Siehe: Rechner für arithmetische Mittel

Median

Der Median ist der Mittelwert aller Daten, geordnet vom kleinsten zum größten. Mit anderen Worten: Der Median teilt den geordneten Datensatz in zwei gleiche Teile.

Die Berechnung des Medians hängt davon ab, ob die Gesamtzahl der Daten gerade oder ungerade ist:

Wenn die Gesamtzahl der Daten ungerade ist, ist der Median der Wert, der genau in der Mitte der Daten liegt. Das heißt der Wert, der an Position (n+1)/2 der sortierten Daten steht.

$Me=x_{\frac{n+1}{2}$

Wenn die Gesamtzahl der Datenpunkte gerade ist, ist der Median der Durchschnitt der beiden Datenpunkte in der Mitte. Das heißt das arithmetische Mittel der Werte, die an den Positionen n/2 und n/2+1 der geordneten Daten gefunden werden.

$Me=\cfrac{x_{\frac{n}{2}}+x_{\frac{n}{2}+1}}{2}$

Gold

$n$

ist die Gesamtzahl der Daten in der Stichprobe und das Symbol Me gibt den Median an.

➤ Siehe: Medianrechner

Mode

In der Statistik ist der Modus der Wert im Datensatz, der die höchste absolute Häufigkeit aufweist, d. h. der Modus ist der am häufigsten wiederholte Wert in einem Datensatz.

Daher gibt es keine spezifische Formel für den Modus. Um jedoch den Modus eines statistischen Datensatzes zu berechnen, zählen Sie einfach, wie oft jedes Datenelement in der Stichprobe vorkommt, und die am häufigsten wiederholten Daten sind der Modus.

Der Modus kann auch als statistischer Modus oder Modalwert bezeichnet werden.

➤ Siehe: Moderechner

Formeln für statistische Streuungsmaße

Standardabweichung

Die Standardabweichung, auch Standardabweichung genannt, ist gleich der Quadratwurzel der Summe der Quadrate der Abweichungen der Datenreihe dividiert durch die Gesamtzahl der Beobachtungen.

Daher lautet die Formel für die Standardabweichung :

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^n(x_i-\overline{x})^2}{n}}$

➤ Siehe: Standardabweichungsrechner

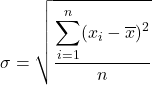
Varianz

Die Varianz entspricht der Summe der Quadrate der Residuen über die Gesamtzahl der Beobachtungen. Die Formel für diese statistische Metrik lautet daher wie folgt:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{x}\right)^2}{n}$

Gold:

$X$

ist die Zufallsvariable, für die Sie die Varianz berechnen möchten.
$x_i$

ist der Datenwert

$i$

.
$n$

ist die Gesamtzahl der Beobachtungen.
$\overline{X}$

ist der Mittelwert der Zufallsvariablen

$X$

.

➤ Siehe: Lückenrechner

Variationskoeffizient

In der Statistik ist der Variationskoeffizient ein Streuungsmaß, mit dem die Streuung eines Datensatzes relativ zu seinem Mittelwert bestimmt wird. Der Variationskoeffizient wird berechnet, indem die Standardabweichung der Daten durch ihren Mittelwert dividiert und dann mit 100 multipliziert wird, um den Wert als Prozentsatz auszudrücken.

$CV=\cfrac{\sigma}{\overline{x}}\cdot 100$

➤ Siehe: Variationskoeffizientenrechner

Ordentlich

Der statistische Bereich ist ein Maß für die Streuung, das die Differenz zwischen dem Maximalwert und dem Minimalwert der Daten in einer Stichprobe angibt. Um den Umfang einer Grundgesamtheit oder statistischen Stichprobe zu berechnen, muss daher der Maximalwert vom Minimalwert abgezogen werden.

$R=\text{M\'ax}-\text{M\'in}$

➤ Siehe: Beispiel für statistische Reichweite

Interquartilbereich

Der Interquartilabstand , auch Interquartilabstand genannt, ist ein Maß für die statistische Streuung, das den Unterschied zwischen dem dritten und dem ersten Quartil angibt.

Um den Interquartilbereich eines statistischen Datensatzes zu berechnen, müssen Sie daher zunächst das dritte und erste Quartil ermitteln und diese dann subtrahieren.

$IQR=Q_3-Q_1$

➤ Siehe: Interquartilbereichsrechner

mittlerer Unterschied

Die mittlere Abweichung , auch mittlere absolute Abweichung genannt, ist der Durchschnitt der absoluten Abweichungen. Die durchschnittliche Abweichung ist daher gleich der Summe der Abweichungen jedes Datenelements vom arithmetischen Mittel geteilt durch die Gesamtzahl der Datenelemente.

$D_{\overline{x}}=\cfrac{\sum_{i=1}^n|x_i-\overline{x}|}{n}$

➤ Siehe: Durchschnittliche Abweichungsrechner

Formeln für statistische Positionsmessungen

Quartile

In der Statistik sind Quartile die drei Werte, die einen Satz geordneter Daten in vier gleiche Teile teilen. Somit machen das erste, zweite und dritte Quartil jeweils 25 %, 50 % und 75 % aller statistischen Daten aus.

Quartile werden durch ein großes Q und den Quartilindex dargestellt, also ist das erste Quartil Q ₁ , das zweite Quartil Q ₂ und das dritte Quartil Q ₃ .

Die Quartilformel lautet:

$\cfrac{k\cdot (n+1)}{4} \qquad k=1, 2, 3$

Bitte beachten Sie: Diese Formel gibt uns die Position des Quartils an, nicht den Wert des Quartils. Das Quartil sind die Daten, die sich an der durch die Formel ermittelten Position befinden.

Manchmal liefert uns das Ergebnis dieser Formel jedoch eine Dezimalzahl. Wir müssen also zwei Fälle unterscheiden, je nachdem, ob das Ergebnis eine Dezimalzahl ist oder nicht:

Wenn das Ergebnis der Formel eine Zahl ohne Dezimalteil ist, ist das Quartil die Daten, die sich an der durch die obige Formel bereitgestellten Position befinden.
Wenn das Formelergebnis eine Zahl mit einem Dezimalteil ist, wird der Quartilwert anhand der folgenden Formel berechnet:

$Q=x_i+d\cdot (x_{i+1}-x_i)$

Dabei sind x _i und x _i+1 die Zahlen der Positionen, zwischen denen sich die durch die erste Formel erhaltene Zahl befindet, und d ist der Dezimalteil der durch die erste Formel erhaltenen Zahl.

➤ Siehe: Quartilrechner

Dezile

In der Statistik sind Dezile die neun Werte, die einen Satz geordneter Daten in zehn gleiche Teile unterteilen. Das erste, zweite, dritte, … Dezil repräsentiert also 10 %, 20 %, 30 %, … der Stichprobe oder Grundgesamtheit.

Dezile werden durch den Großbuchstaben D und den Dezilindex dargestellt, d. h. das erste Dezil ist D ₁ , das zweite Dezil ist D ₂ , das dritte Dezil ist D ₃ usw.

Die Dezilformel lautet wie folgt:

$\cfrac{k\cdot (n+1)}{10} \qquad k=1, 2, 3,4,5,6,7,8,9$

Bitte beachten Sie: Diese Formel sagt uns die Position des Dezils, nicht den Wert des Dezils. Das Dezil sind die Daten, die sich an der durch die Formel ermittelten Position befinden.

Manchmal liefert uns das Ergebnis dieser Formel jedoch eine Dezimalzahl. Daher müssen wir zwei Fälle unterscheiden, je nachdem, ob das Ergebnis eine Dezimalzahl ist oder nicht:

Wenn das Ergebnis der Formel eine Zahl ohne Dezimalteil ist, sind das Dezil die Daten, die sich an der durch die obige Formel angegebenen Position befinden.
Wenn das Ergebnis der Formel eine Zahl mit Dezimalteil ist, wird der Dezilwert nach folgender Formel berechnet:

$D=x_i+d\cdot (x_{i+1}-x_i)$

Dabei sind x _i und x _i+1 die Zahlen der Positionen, zwischen denen sich die durch die erste Formel erhaltene Zahl befindet, und d ist der Dezimalteil der durch die erste Formel erhaltenen Zahl.

➤ Siehe: Dezilrechner

Perzentile

In der Statistik sind Perzentile die Werte, die einen Satz geordneter Daten in hundert gleiche Teile teilen. Ein Perzentil gibt also den Wert an, unter den ein Prozentsatz des Datensatzes fällt.

Perzentile werden durch den Großbuchstaben P und den Perzentilindex dargestellt, d. h. das erste Perzentil ist P ₁ , das 40. Perzentil ist P ₄₀ , das 79. Perzentil ist P ₇₉ usw.

Die Perzentilformel lautet:

$\cfrac{k\cdot (n+1)}{100} \qquad k=1, 2, 3,\ldots ,97,98,99$

Bitte beachten Sie: Diese Formel sagt uns die Position des Perzentils, nicht jedoch seinen Wert. Das Perzentil sind die Daten, die sich an der durch die Formel ermittelten Position befinden.

Manchmal liefert uns das Ergebnis dieser Formel jedoch eine Dezimalzahl. Daher müssen wir zwei Fälle unterscheiden, je nachdem, ob das Ergebnis eine Dezimalzahl ist oder nicht:

Wenn das Ergebnis der Formel eine Zahl ohne Dezimalteil ist, entspricht das Perzentil den Daten, die sich an der in der obigen Formel angegebenen Position befinden.
Wenn das Formelergebnis eine Zahl mit Dezimalteil ist, wird der genaue Perzentilwert anhand der folgenden Formel berechnet:

$P=x_i+d\cdot (x_{i+1}-x_i)$

Dabei sind x _i und x _i+1 die Zahlen der Positionen, zwischen denen sich die durch die erste Formel erhaltene Zahl befindet, und d ist der Dezimalteil der durch die erste Formel erhaltenen Zahl.

➤ Siehe: Perzentilrechner

Formeln zur statistischen Formmessung

Asymmetriekoeffizient

Der Schiefekoeffizient oder Schiefeindex ist ein statistischer Koeffizient, der zur Bestimmung der Schiefe einer Verteilung verwendet wird. Durch die Berechnung des Asymmetriekoeffizienten können Sie also die Art der Asymmetrie der Verteilung ermitteln, ohne eine grafische Darstellung davon erstellen zu müssen.

Die Formel für den Asymmetriekoeffizienten lautet wie folgt:

$\displaystyle\gamma_1=\frac{\overline{x}_3}{\sigma^3}$

Entsprechend kann eine der beiden folgenden Formeln zur Berechnung des Fisher-Asymmetriekoeffizienten verwendet werden:

$\displaystyle\gamma_1=\frac{\displaystyle \sum_{i=1}^N\left(x_i-\overline{x}\right)^3}{n\cdot \sigma ^3}$

$\displaystyle\gamma_1=\frac{\operatorname{E}[X^3] - 3\cdot \overline{x}\cdot \sigma^2 - \overline{x}^3}{\sigma^3}$

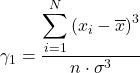
Gold

$E$

ist die mathematische Erwartung,

$\overline{x}$

das arithmetische Mittel,

$\sigma$

die Standardabweichung und

$n$

die Gesamtzahl der Daten.

➤ Siehe: Asymmetriekoeffizient

Kurtosis-Koeffizient

Kurtosis, auch Schärfe genannt, gibt an, wie konzentriert eine Verteilung um ihren Mittelwert herum ist. Mit anderen Worten: Kurtosis gibt an, ob eine Verteilung steil oder flach ist. Konkret gilt: Je größer die Kurtosis einer Verteilung, desto steiler (oder schärfer) ist sie.

Die Formel für den Kurtosis-Koeffizienten lautet wie folgt:

$\displaystyle g_2=\frac{1}{n}\cdot\frac{\displaystyle \sum_{i=1}^n(x_i-\overline{x})^4}{\sigma^4}-3$

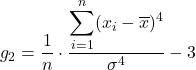
Gold

$x_i$

ist der Wert, der der Beobachtung entspricht

$i$

$\overline{x}$

das arithmetische Mittel,

$\sigma$

die Standardabweichung und

$n$

die Gesamtzahl der Daten.

➤ Siehe: Abflachungskoeffizientenrechner

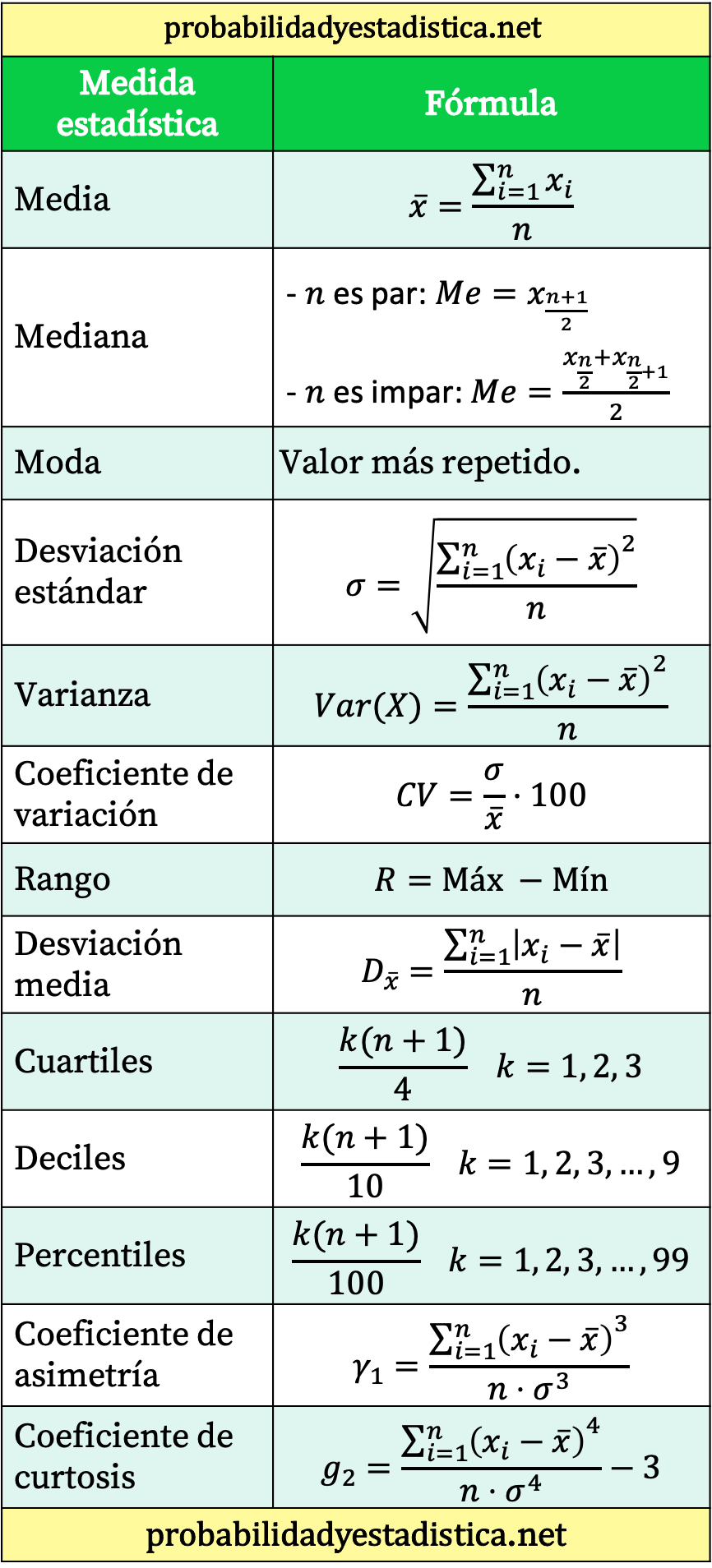
Übersichtstabelle aller statistischen Formeln

Abschließend hinterlassen wir Ihnen eine Tabelle, die die wichtigsten statistischen Formeln zusammenfasst.

➤ Siehe: Wahrscheinlichkeitsformeln

Über den Autor

Dr. Benjamin Anderson

Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen

Formeln für statistische Maße der zentralen Tendenz

Halb

Median

Mode

Formeln für statistische Streuungsmaße

Standardabweichung

Varianz

Variationskoeffizient

Ordentlich

Interquartilbereich

mittlerer Unterschied

Formeln für statistische Positionsmessungen

Quartile

Dezile

Perzentile

Formeln zur statistischen Formmessung

Asymmetriekoeffizient

Kurtosis-Koeffizient

Übersichtstabelle aller statistischen Formeln

Über den Autor

Dr. Benjamin Anderson

Einen Kommentar hinzufügen