Rang (statistik)
In diesem Artikel erklären wir, was Spannweite in der Statistik ist und wie sie berechnet wird. Sie finden eine gelöste Übung zum Umfang eines Datensatzes und abschließend zeigen wir Ihnen, wozu er dient und wann er verwendet werden sollte.
Was ist Reichweite in der Statistik?
In der Statistik ist die Reichweite ein Maß für die Streuung, das die Differenz zwischen dem Maximalwert und dem Minimalwert der Daten einer Stichprobe angibt. Um den Umfang einer Grundgesamtheit oder statistischen Stichprobe zu berechnen, muss daher der Maximalwert vom Minimalwert abgezogen werden.
Wenn beispielsweise der Maximalwert eines Datensatzes 9 und der Minimalwert 2 beträgt, beträgt der Bereich dieser statistischen Stichprobe 7 (9-2=7).
Der statistische Bereich wird auch als Messumfang oder Messbereich bezeichnet.
Die Reichweite ist also ein Maß für die Streuung mit Varianz, Standardabweichung (oder Standardabweichung), mittlerer Abweichung und Variationskoeffizient.
So berechnen Sie die Reichweite in der Statistik
Der Bereich einer Stichprobe wird durch Subtrahieren der Extremwerte der statistischen Stichprobendaten berechnet, d. h . der Bereich einer Stichprobe ist gleich dem Maximalwert aller Daten abzüglich des Minimalwerts .
Daher lautet die Formel zur Berechnung der statistischen Reichweite eines Datensatzes:
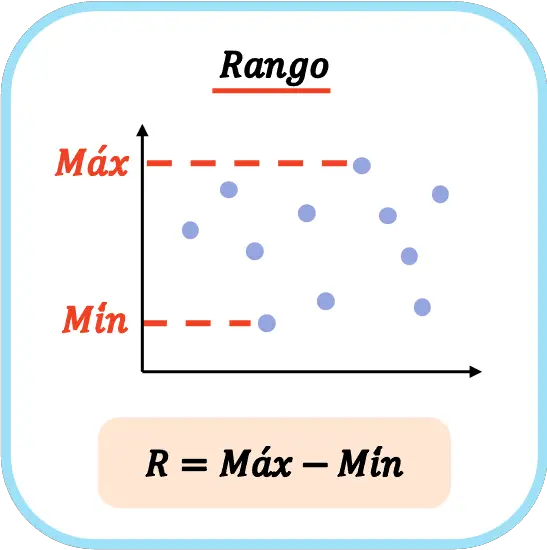
In der Statistik wird häufig das Symbol für ein großes R verwendet, um den Umfang einer Datenreihe anzugeben.
Die Berechnung der Reichweite eines Datensatzes ist daher recht einfach, da lediglich die Differenz zwischen den Extremwerten ermittelt werden muss. Das Einzige, worauf Sie achten müssen, ist, dass Sie die maximalen und minimalen Daten korrekt angeben und keine Zahlen vergessen.
Beispielbereich (Statistik)
Nachdem Sie die Definition des Bereichs in der Statistik kennengelernt haben, finden Sie unten ein ausgearbeitetes Beispiel, damit Sie sehen können, wie der Bereich eines Datensatzes ermittelt wird.
- Ein Unternehmen möchte die mit seinem Flaggschiffprodukt in den letzten zwanzig Jahren erzielten Umsätze statistisch analysieren. Dazu werden Sie aufgefordert, mehrere statistische Kennzahlen zu berechnen, einschließlich des Rankings. Wenn die Verkäufe des Produkts wie in der folgenden Tabelle dargestellt sind, welchen Umfang hat dieser Datensatz?
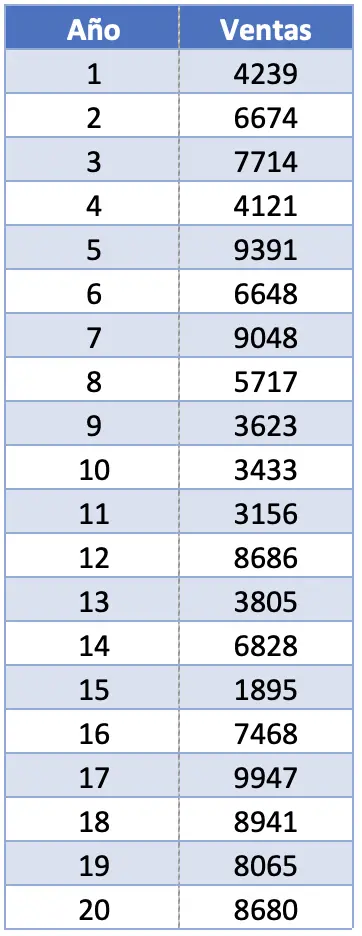
In dieser Übung haben wir 20 Beobachtungen. In Wirklichkeit spielt die Gesamtzahl der Beobachtungen bei der Berechnung des Umfangs einer Stichprobe keine Rolle, da uns nur der größte und der kleinste Wert interessieren.
Wir müssen daher die oben gezeigte Formel verwenden, um den Umfang dieser statistischen Stichprobe zu ermitteln.
![]()
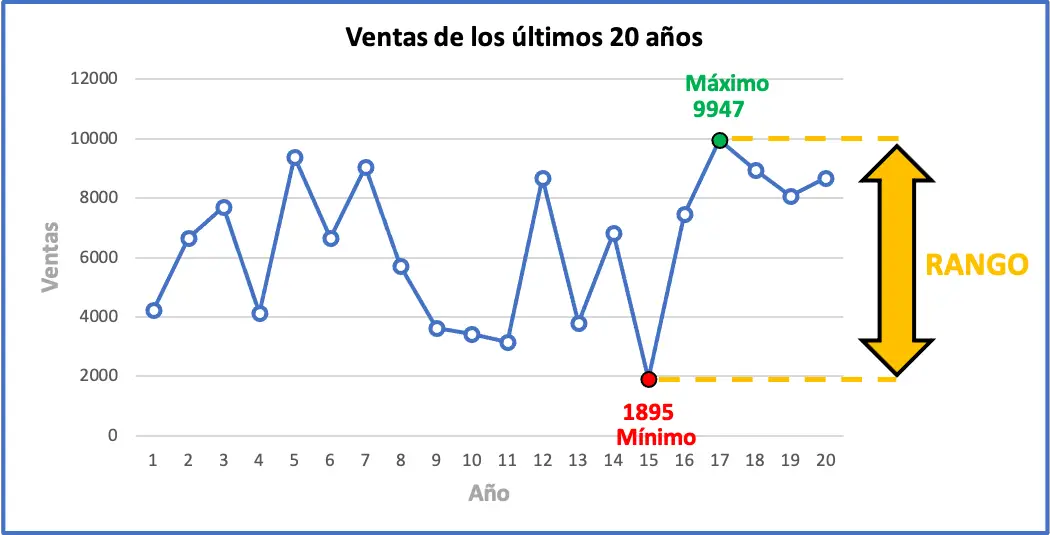
Der Maximalwert des Intervalls beträgt 9947 verkaufte Einheiten und der Minimalwert 1895. Daher müssen wir diese beiden Werte subtrahieren, um den Bereich des Datensatzes zu ermitteln:
![]()
Damit beträgt die maximale Verkaufsveränderung in den letzten Jahren 8.052 Einheiten. Unten können Sie alle Trainingsdaten zusammen mit ihrem statistischen Bereich grafisch sehen. Die Grafik wird Ihnen wahrscheinlich dabei helfen, die Bedeutung des Bereichs zu verstehen.
Wofür wird der statistische Bereich verwendet?
Um das Verständnis des Begriffs „Ausdehnung“ in der Statistik zu vervollständigen, sehen wir uns an, wofür er verwendet wird und wie dieses Streuungsmaß zu interpretieren ist.
In der Statistik zeigt der Bereich die Differenz zwischen dem Maximalwert und dem Minimalwert eines Datensatzes an. Daher ist die Reichweite ein Maß, das verwendet wird, um die Gesamtstreuung eines Datensatzes anzugeben .
Wenn Sie den Bereichswert eines Datensatzes kennen, kennen Sie die maximale Differenz zwischen zwei beliebigen Beobachtungen in diesem Satz, sodass Sie eine Vorstellung davon bekommen können, ob die Daten verstreut oder nahe beieinander liegen. Generell ist es von Vorteil, wenn die Reichweite möglichst gering ist, da dadurch die Streuung geringer ist und die Berechnungen daher genauer sind.
Beispielsweise kann es sich bei der Reichweite um eine Messung handeln, die den Vergleich zwischen zwei verschiedenen Proben ermöglicht, da sie es Ihnen ermöglicht, sich ein Bild von der Streuung der Proben zu machen.
Bei der Interpretation des statistischen Bereichs ist jedoch Vorsicht geboten, da dieser irreführend sein kann. Es kann sein, dass ein Datensatz tatsächlich eine sehr geringe Streuung aufweist. Wenn es jedoch einen Ausreißer innerhalb der Stichprobe gibt, ist der Bereich sehr groß und spiegelt daher die Streuung der Stichprobe nicht richtig wider.
Darüber hinaus ist es nicht dasselbe, dass eine Stichprobe, deren Werte in der Größenordnung von Zehnern liegen, einen Rang von 5 hat, als dass eine Stichprobe, deren Werte in der Größenordnung von Tausenden liegen, denselben Rang hat. Selbst wenn beide Bereiche die gleiche Zahl haben, ist die erste Stichprobe logischerweise viel stärker gestreut als die zweite.
Zusammenfassend lässt sich sagen, dass die Reichweite ein nützliches statistisches Maß für die Analyse der Streuung eines Datensatzes ist. Um die Daten jedoch richtig zu interpretieren, müssen auch andere Metriken berechnet werden.