Probengröße
In diesem Artikel wird erklärt, was die Stichprobengröße ist und warum sie in der Statistik wichtig ist. Darüber hinaus erfahren Sie, wie Sie die entsprechende Stichprobengröße berechnen und eine gelöste Übung, damit Sie sehen können, wie es geht.
Wie groß ist die Stichprobengröße?
Die Stichprobengröße (oder Stichprobengröße ) ist die Anzahl der Personen, aus denen die Stichprobe einer Studie besteht. In der Statistik ist die Stichprobengröße wichtig, damit die Stichprobe repräsentativ für die gesamte Bevölkerung ist.
Daher muss die Stichprobengröße einer statistischen Studie groß genug sein, um die Merkmale der gesamten Bevölkerung darzustellen. Andererseits darf die Stichprobengröße nicht übermäßig groß sein, da die Forschung dann teurer wird. Zusammenfassend lässt sich sagen, dass die Stichprobengröße angemessen sein sollte, weder zu groß noch zu klein.
Wenn wir beispielsweise die Höhe eines Landes analysieren möchten, können wir nicht nach der Größe aller Einwohner des Landes fragen, da die Erhebung viel Zeit in Anspruch nehmen und zu teuer wäre. Daher ist es notwendig, eine Zufallsstichprobe durchzuführen und nur eine repräsentative Stichprobe der Bevölkerung zu befragen.
Und wie können wir die geeignete Stichprobengröße ermitteln? Im nächsten Abschnitt erfahren Sie, wie Sie anhand der Forschungsanforderungen die geeignete Stichprobengröße bestimmen.
So berechnen Sie die Stichprobengröße
Zur Schätzung eines Mittelwerts entspricht die erforderliche Stichprobengröße dem Quadrat von Z α/2 multipliziert mit der Standardabweichung (σ) dividiert durch die gewünschte Fehlerspanne (e). Die Formel zur Berechnung der Stichprobengröße lautet daher:
![]()
Gold:
-

ist die Stichprobengröße.
-
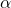
ist das gewünschte Signifikanzniveau. Unter Berücksichtigung dessen
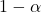
ist das gewünschte Konfidenzniveau.
-

ist das Quantil der Standardnormalverteilung, das einer Wahrscheinlichkeit von α/2 entspricht. Bei großen Stichprobengrößen und einem Konfidenzniveau von 95 % liegt er normalerweise nahe bei 1,96 und bei einem Konfidenzniveau von 99 % normalerweise nahe bei 2,576.
-

ist die Standardabweichung.
Beachten Sie, dass in dieser Formel davon ausgegangen wird, dass die Populationsgröße unendlich ist, d. h. die Populationsgröße ist sehr groß oder unbekannt.
Hinweis: Die obige Formel wird aus dem Konfidenzformelintervall für den Mittelwert abgeleitet.
Beispiel für die Berechnung der Stichprobengröße
In diesem Abschnitt berechnen wir beispielhaft die geeignete Stichprobengröße für eine statistische Erhebung.
- Wir wissen, dass die Standardabweichung einer Grundgesamtheit etwa 15 beträgt, aber wir kennen ihren Mittelwert nicht, deshalb möchten wir eine Studie durchführen, um den Mittelwert zu schätzen. Welche Stichprobengröße benötigen wir, wenn wir eine Fehlermarge von ±2 mit einem Konfidenzniveau von 95 % wünschen?
Wie wir oben gesehen haben, lautet die Formel zur Berechnung der Stichprobengröße:
![]()
In diesem Fall beträgt das gewünschte Konfidenzniveau 95 %, sodass der entsprechende Z α/2 -Wert 1,96 beträgt.
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}Z_{\alpha/2}= \ \color{orange}\bm{?}\\[4ex]Z_{0,025}=1,96\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-54dda39d0da5b29f2d25728b89565859_l3.png)
Da wir nun endlich wissen, wie viel alle Parameter wert sind, setzen wir ihre Werte in die Formel ein und berechnen die Stichprobengröße:
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle n&=\left(\frac{Z_{\alpha/2}\cdot\sigma}{e}\right)^2\\[2ex] n&=\left(\frac{1,96\cdot 15}{2}\right)^2\\[2ex] n&=216,09 \approx 217 \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-dd8e2d30042f759051fb52c5c55ade44_l3.png)
Kurz gesagt, um den Bevölkerungsmittelwert mit den gewünschten Anforderungen zu schätzen, benötigen wir mindestens eine Stichprobe von 217 Personen.
Stichprobengröße, Konfidenzniveau und Fehlermarge
Abhängig vom Grad der Konfidenz und der erforderlichen Fehlermarge variiert die erforderliche Stichprobengröße. Somit hängen Stichprobengröße, Konfidenzniveau und Fehlermarge wie folgt zusammen:
- Die Stichprobengröße und das Konfidenzniveau sind direkt proportional. Das heißt, wenn das Konfidenzniveau steigt, nimmt auch die Stichprobengröße zu.
- Stichprobengröße und Fehlerspanne sind umgekehrt proportional. Wenn also die Fehlerspanne zunimmt, nimmt die Stichprobengröße ab.
- Daher kann eine Vergrößerung der Stichprobengröße das Konfidenzniveau erhöhen oder die Fehlerquote verringern.
Andere Formeln für die Stichprobengröße
Abhängig vom zu schätzenden Parameter variiert die Formel für die erforderliche Stichprobengröße geringfügig. Daher werden wir in diesem Abschnitt andere Formeln sehen, die in einigen Sonderfällen zur Berechnung der Stichprobengröße nützlich sein können.
Stichprobengröße eines Anteils
Die Formel zur Berechnung der Stichprobengröße, die zur Schätzung eines Anteils (p) erforderlich ist, lautet:
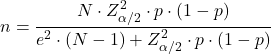
Stichprobengröße einer Wahrscheinlichkeit
Wenn Sie eine Wahrscheinlichkeit schätzen möchten, empfiehlt es sich, die folgende Formel zu verwenden, um den erforderlichen Stichprobenumfang zu ermitteln:
![]()
Stichprobengröße zum Vergleich zweier unabhängiger Mittelwerte
Die Formel zur Berechnung der Stichprobengröße beim Vergleich zweier unabhängiger Mittelwerte mit einem gegebenen α-Risiko und β-Risiko lautet wie folgt:
![]()
Gold
![]()
ist die Differenz zwischen den beiden Mittelwerten der Alternativhypothese.
Stichprobengröße zum Vergleich zweier gepaarter Mittelwerte
Wenn Sie zwei gepaarte Mittelwerte mit festem Fehler α und Fehler β vergleichen möchten, lautet die Formel zur Ermittlung der Anzahl der Beobachtungen in der Stichprobe:
![]()
Gold
![]()
ist die Differenz zwischen den beiden gepaarten Mittelwerten der Alternativhypothese und
![]()
Dabei handelt es sich um die Varianz der Unterschiede zwischen zwei Messungen desselben Individuums.