Was ist eine stichprobenverteilung?

Stellen Sie sich vor, es gibt eine Population von 10.000 Delfinen und das durchschnittliche Gewicht eines Delfins in dieser Population beträgt 300 Pfund.

Wenn wir eine einfache Zufallsstichprobe von 50 Delfinen aus dieser Population ziehen, könnten wir feststellen, dass das Durchschnittsgewicht der Delfine in dieser Stichprobe 305 Pfund beträgt.

Wenn wir dann eine weitere einfache Zufallsstichprobe von 50 Delfinen nehmen, könnten wir feststellen, dass das durchschnittliche Gewicht der Delfine in dieser Stichprobe 295 Pfund beträgt.

Wenn wir eine einfache Zufallsstichprobe von 50 Delfinen nehmen, ist es wahrscheinlich, dass das Durchschnittsgewicht der Delfine in der Stichprobe nahe am Bevölkerungsdurchschnitt von 300 Pfund liegt, aber nicht genau 300 Pfund.

Stellen wir uns vor, wir nehmen 200 einfache Zufallsstichproben von 50 Delfinen aus dieser Population und erstellen ein Histogramm des Durchschnittsgewichts jeder Stichprobe:

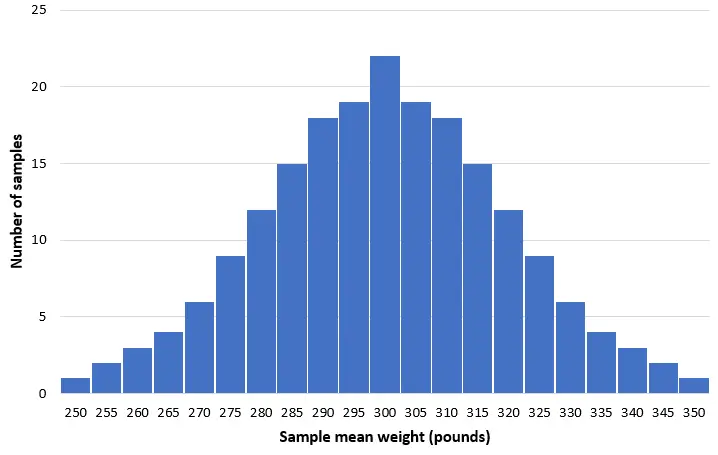
In den meisten Proben liegt das Durchschnittsgewicht bei etwa 300 Pfund. In seltenen Fällen können wir eine Probe voller kleiner Delfine entnehmen, deren Durchschnittsgewicht nur 250 Pfund beträgt. Oder wir nehmen eine Probe voller Tümmler, die durchschnittlich 350 Pfund wiegen. Im Allgemeinen ist die Verteilung der Stichprobenmittelwerte annähernd normal, wobei sich das Verteilungszentrum im wahren Zentrum der Grundgesamtheit befindet.

Diese Verteilung der Stichprobenmittelwerte wird als Stichprobenverteilung des Mittelwerts bezeichnet und weist die folgenden Eigenschaften auf:

_µx = µ

Dabei ist μ _x der Stichprobenmittelwert und μ der Populationsmittelwert.

_σx = σ/√n

Dabei ist σ _x die Stichprobenstandardabweichung, σ die Grundgesamtheitsstandardabweichung und n die Stichprobengröße.

Wir wissen beispielsweise, dass das Durchschnittsgewicht dieser Delfinpopulation μ = 300 beträgt. Der Mittelwert der Stichprobenverteilung beträgt also μ _x = 300 .

Nehmen wir an, wir wissen auch, dass die Populationsstandardabweichung 18 Pfund beträgt. Die Stichprobenstandardabweichung beträgt daher σ _x = 18/ √50 = 2,546 .

Stichprobenverteilung des Anteils

Betrachten Sie die gleiche Population von 10.000 Delfinen. Gehen Sie davon aus, dass 10 % der Delfine schwarz und der Rest grau sind. Nehmen wir an, wir nehmen eine einfache Zufallsstichprobe von 50 Delfinen und stellen fest, dass 14 % der Delfine in dieser Stichprobe schwarz sind. Als nächstes nehmen wir eine weitere einfache Zufallsstichprobe von 50 Delfinen und stellen fest, dass 8 % der Delfine in dieser Stichprobe schwarz sind.

Stellen Sie sich vor, wir nehmen 200 einfache Zufallsstichproben von 50 Delfinen aus dieser Population und erstellen ein Histogramm des Anteils schwarzer Delfine in jeder Stichprobe:

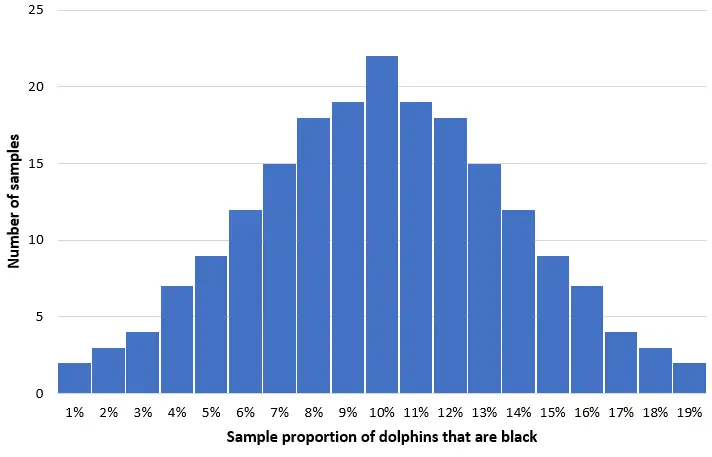
In den meisten Proben wird der Anteil schwarzer Delfine nahe an der tatsächlichen Population von 10 % liegen. Die Verteilung des Stichprobenanteils schwarzer Delfine wird annähernd normal sein, wobei das Verteilungszentrum im wahren Zentrum der Population liegt.

Diese Verteilung der Stichprobenanteile wird als Stichprobenanteilsverteilung bezeichnet und weist die folgenden Eigenschaften auf:

_µp = P

Dabei ist p der Stichprobenanteil und P der Bevölkerungsanteil.

σ _p = √ (P)(1-P) / n

Dabei ist P der Bevölkerungsanteil und n die Stichprobengröße.

Wir wissen beispielsweise, dass in dieser Delfinpopulation der tatsächliche Anteil der schwarzen Delfine 10 % = 0,1 beträgt. Somit beträgt der Mittelwert der Anteilsstichprobenverteilung μ _p = 0,1 .

Nehmen wir an, wir wissen auch, dass die Populationsstandardabweichung 18 Pfund beträgt. Somit beträgt die Stichprobenstandardabweichung σ _p = √ (P)(1-P) / n = √ (.1)(1-.1) / 50 = .042 .

Normalität etablieren

Um die oben genannten Formeln verwenden zu können, muss die Stichprobenverteilung normal sein.

Nach dem zentralen Grenzwertsatz ist die Stichprobenverteilung eines Stichprobenmittelwerts annähernd normal, wenn die Stichprobengröße groß genug ist, auch wenn die Grundgesamtheitsverteilung nicht normal ist . In den meisten Fällen halten wir eine Stichprobengröße von 30 oder mehr für ausreichend.

Die Stichprobenverteilung eines Stichprobenanteils ist ungefähr normal, wenn die erwartete Anzahl an Erfolgen und Misserfolgen jeweils mindestens 10 beträgt.

Beispiele

Wir können Stichprobenverteilungen verwenden, um Wahrscheinlichkeiten zu berechnen.

Beispiel 1: Eine bestimmte Maschine erstellt Cookies. Die Gewichtsverteilung dieser Kekse ist mit einem Mittelwert von 10 Unzen und einer Standardabweichung von 2 Unzen rechtsschief. Wenn wir eine einfache Zufallsstichprobe von 100 von dieser Maschine hergestellten Keksen nehmen, wie groß ist dann die Wahrscheinlichkeit, dass das durchschnittliche Gewicht der Kekse in dieser Stichprobe weniger als 9,8 Unzen beträgt?

Schritt 1: Normalität herstellen.

Wir müssen sicherstellen, dass die Stichprobenverteilung der Stichprobenmittelwerte normal ist. Da unsere Stichprobengröße gemäß dem zentralen Grenzwertsatz größer oder gleich 30 ist, können wir davon ausgehen, dass die Stichprobenverteilung der Stichprobenmittelwerte normal ist.

Schritt 2: Ermitteln Sie den Mittelwert und die Standardabweichung der Stichprobenverteilung.

_µx = µ

_σx = σ/√n

μ _x = 10 Unzen

σ _x = 2/ √100 = 2/10 = 0,2 Unzen

Schritt 3: Verwenden Sie den Z-Score-Flächenrechner, um die Wahrscheinlichkeit zu bestimmen, dass das durchschnittliche Keksgewicht in dieser Probe weniger als 9,8 Unzen beträgt.

Geben Sie die folgenden Zahlen in den Z-Score-Flächenrechner ein. Sie können „Raw Score 2“ leer lassen, da wir in diesem Beispiel nur eine Zahl finden.

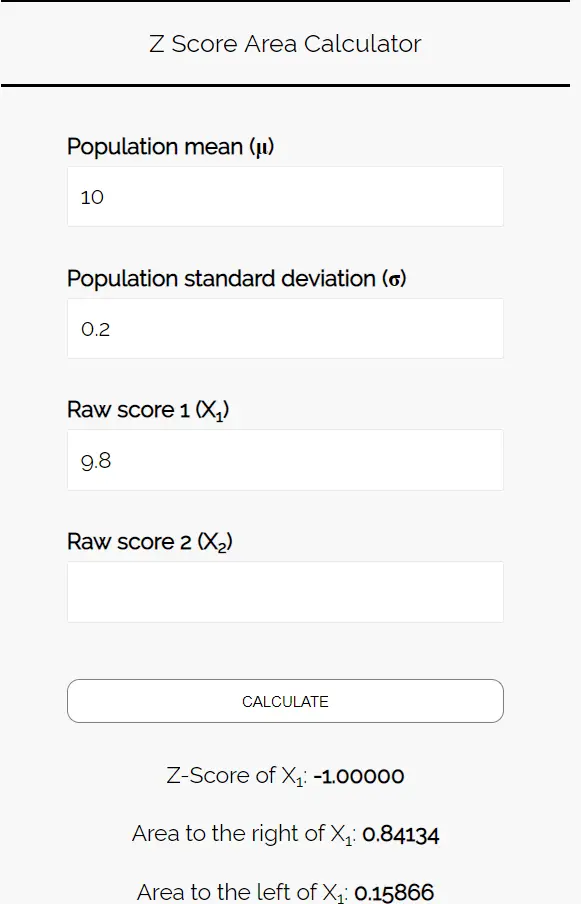
Da wir die Wahrscheinlichkeit wissen möchten, dass das durchschnittliche Gewicht der Kekse in dieser Stichprobe weniger als 9,8 Unzen beträgt, interessiert uns der Bereich links von 9,8. Der Rechner sagt uns, dass diese Wahrscheinlichkeit 0,15866 beträgt.

Beispiel 2: Laut einer schulweiten Studie bevorzugen 87 % der Schüler einer bestimmten Schule Pizza gegenüber Eis. Nehmen wir an, wir nehmen eine einfache Zufallsstichprobe von 200 Studenten. Wie groß ist die Wahrscheinlichkeit, dass der Anteil der Studierenden, die Pizza bevorzugen, unter 85 % liegt?

Schritt 1: Normalität herstellen.

Denken Sie daran, dass die Stichprobenverteilung eines Stichprobenanteils annähernd normal ist, wenn die erwartete Anzahl von „Erfolgen“ und „Misserfolgen“ jeweils mindestens 10 beträgt.

In diesem Fall beträgt die erwartete Anzahl der Studierenden, die Pizza bevorzugen, 87 % * 200 Studierende = 174 Studierende. Die erwartete Zahl der Studierenden, die keine Pizza bevorzugen, beträgt 13 % * 200 Studierende = 26 Studierende. Da beide Zahlen mindestens 10 betragen, können wir davon ausgehen, dass die Stichprobenverteilung des Anteils der Schüler, die Pizza bevorzugen, annähernd normal ist.

Schritt 2: Ermitteln Sie den Mittelwert und die Standardabweichung der Stichprobenverteilung.

_µp = P

σ _p = √ (P)(1-P) / n

_µp = 0,87

σ _p = √ (0,87)(1-0,87) / 200 = 0,024

Schritt 3: Verwenden Sie den Z-Score-Flächenrechner, um die Wahrscheinlichkeit zu bestimmen, dass der Anteil der Schüler, die Pizza bevorzugen, weniger als 85 % beträgt.

Geben Sie die folgenden Zahlen in den Z-Score-Flächenrechner ein. Sie können „Raw Score 2“ leer lassen, da wir in diesem Beispiel nur eine Zahl finden.

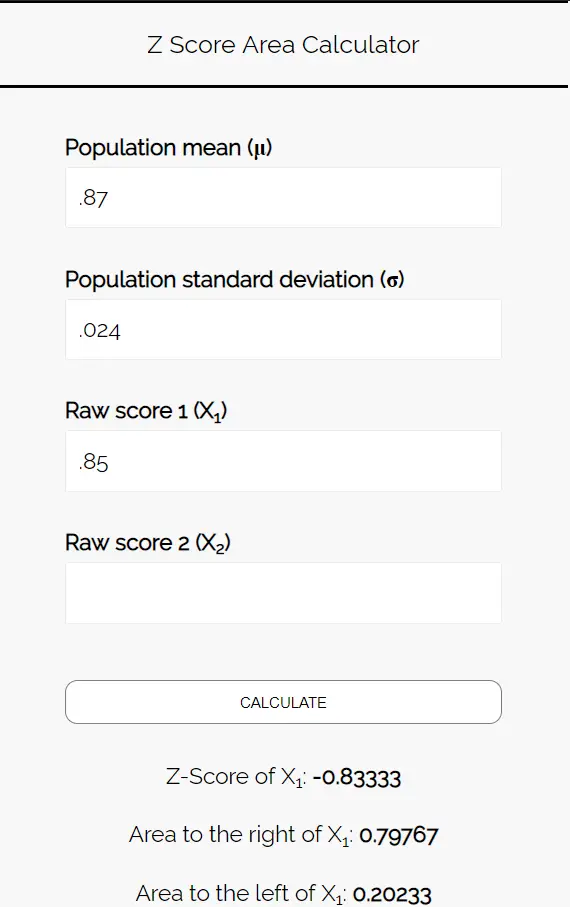
Da wir wissen wollen, mit welcher Wahrscheinlichkeit der Anteil der Schüler, die Pizza bevorzugen, weniger als 85 % beträgt, interessiert uns der Bereich links von 0,85. Der Rechner sagt uns, dass diese Wahrscheinlichkeit 0,20233 beträgt.