Stichprobenverteilung

Von August 3, 2023 Statistiken Keine Kommentare

In diesem Artikel wird erklärt, was Stichprobenverteilung in der Statistik ist und wofür sie verwendet wird. So finden Sie die Bedeutung einer Stichprobenverteilung, ein konkretes Beispiel einer Stichprobenverteilung und darüber hinaus die Formeln für die gängigsten Arten von Stichprobenverteilungen.

Wie ist die Stichprobenverteilung?

Die Stichprobenverteilung oder Stichprobenverteilung ist die Verteilung, die sich aus der Berücksichtigung aller möglichen Stichproben aus einer Grundgesamtheit ergibt. Mit anderen Worten: Die Stichprobenverteilung ist die Verteilung, die man durch die Berechnung eines Stichprobenparameters aller möglichen Stichproben aus einer Grundgesamtheit erhält.

Wenn wir beispielsweise alle möglichen Stichproben aus einer statistischen Grundgesamtheit extrahieren und den Mittelwert jeder Stichprobe berechnen, bildet die Menge der Stichprobenmittelwerte eine Stichprobenverteilung. Genauer gesagt, da der berechnete Parameter das arithmetische Mittel ist, handelt es sich um die Stichprobenverteilung des Mittelwerts.

In der Statistik wird die Stichprobenverteilung verwendet, um die Wahrscheinlichkeit zu berechnen, dass man sich bei der Untersuchung einer einzelnen Stichprobe dem Wert des Grundgesamtheitsparameters annähert. In ähnlicher Weise ermöglicht uns die Stichprobenverteilung, den Stichprobenfehler für eine gegebene Stichprobengröße abzuschätzen.

Beispiel für eine Stichprobenverteilung

Nachdem wir nun die Definition der Stichprobenverteilung kennen, schauen wir uns ein einfaches Beispiel an, um das Konzept vollständig zu verstehen.

  • In eine Schachtel legen wir drei Kugeln und auf jede Kugel ist eine Zahl von eins bis drei geschrieben, so dass eine Kugel die Zahl 1, eine andere Kugel die Zahl 2 und die letzte Kugel die Zahl 3 hat. Für eine Stichprobe der Größe n = 2 berechnet die Wahrscheinlichkeiten der Stichprobenverteilung des Mittelwerts, wenn Stichproben mit Ersetzung ausgewählt werden.

Die Proben werden mit Ersatz ausgewählt, das heißt, die zur Auswahl des ersten Elements der Probe aufgenommene Kugel wird in die Box zurückgelegt und kann bei der zweiten Extraktion erneut ausgewählt werden. Daher sind alle möglichen Stichproben aus der Bevölkerung:

1.1 1.2 1.3
2.1 2.2 2.3
3.1 3.2 3.3

Daher berechnen wir das arithmetische Mittel jeder möglichen Stichprobe:

(1,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{11}=\cfrac{1+1}{2}=1

(1,2) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{12}=\cfrac{1+2}{2}=1,5

(1,3) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{13}=\cfrac{1+3}{2}=2

(2,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{21}=\cfrac{2+1}{2}=1,5

(2,2) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{22}=\cfrac{2+2}{2}=2

(2,3) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{23}=\cfrac{2+3}{2}=2,5

(3,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{31}=\cfrac{3+1}{2}=2

(3,2) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{32}=\cfrac{3+2}{2}=2,5

(3,3) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{33}=\cfrac{3+3}{2}=3

Daher sind die Wahrscheinlichkeiten, jeden Wert des Stichprobenmittelwerts zu erhalten, wenn eine Zufallsstichprobe aus der Grundgesamtheit ausgewählt wird, wie folgt:

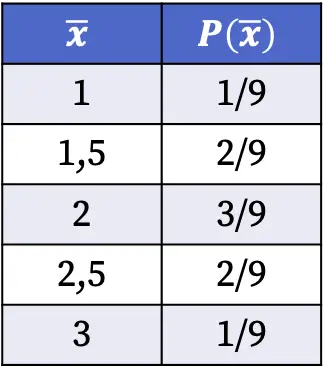
Beispiel für eine Beispielverteilungstabelle

Die Wahrscheinlichkeiten der in der Tabelle oben gezeigten Stichprobenverteilung wurden berechnet, indem die Anzahl der Stichproben mit diesem Mittelwert durch die Gesamtzahl der möglichen Fälle dividiert wurde. Beispiel: Der Stichprobenmittelwert beträgt in zwei von neun möglichen Fällen 1,5, daher ist P(1,5)=2/9.

Arten von Stichprobenverteilungen

Stichprobenverteilungen (oder Stichprobenverteilungen) können basierend auf dem Stichprobenparameter, aus dem sie ermittelt wurden, klassifiziert werden. Die häufigsten Verteilungsarten sind also die folgenden:

  • Stichprobenverteilung des Mittelwerts : Dies ist die Stichprobenverteilung, die sich aus der Berechnung des arithmetischen Mittels jeder Stichprobe ergibt.
  • Proportionale Stichprobenverteilung : Hierbei handelt es sich um die Stichprobenverteilung, die durch Berechnen des Anteils aller Stichproben ermittelt wird.
  • Stichprobenvarianzverteilung : Dies ist die Stichprobenverteilung, die die Menge aller Varianzen in der Stichprobe bildet.
  • Differenz der Mittelwerte der Stichprobenverteilung : ist die Stichprobenverteilung, die sich aus der Berechnung der Differenz zwischen den Mittelwerten aller möglichen Stichproben aus zwei verschiedenen Grundgesamtheiten ergibt.
  • Differenz in den Proportionen der Stichprobenverteilung : ist die Stichprobenverteilung, die durch Subtrahieren aller möglichen Stichprobenanteile von zwei Grundgesamtheiten erhalten wird.

Die einzelnen Arten der Stichprobenverteilung werden im Folgenden ausführlicher erläutert.

Stichprobenverteilung des Mittelwerts

Gegeben sei eine Grundgesamtheit, die einer normalen Wahrscheinlichkeitsverteilung mit Mittelwert folgt

\mu

und Standardabweichung

\sigma

und Größenproben werden extrahiert

n

, wird die Stichprobenverteilung des Mittelwerts auch durch eine Normalverteilung mit den folgenden Merkmalen definiert:

\begin{array}{c}\mu_{\overline{x}}=\mu \qquad \sigma_{\overline{x}}=\cfrac{\sigma}{\sqrt{n}}\\[4ex]\displaystyle N_{\overline{x}}\left(\mu, \frac{\sigma}{\sqrt{n}}\right) \end{array}

Gold

\mu_{\overline{x}}

ist der Mittelwert der Stichprobenverteilung des Mittelwerts und

\sigma_{\overline{x}}

ist seine Standardabweichung. Außerdem,

\cfrac{\sigma}{\sqrt{n}}

ist der Standardfehler der Stichprobenverteilung.

Hinweis: Wenn die Grundgesamtheit keiner Normalverteilung folgt, aber die Stichprobengröße groß ist (n>30), kann die Stichprobenverteilung des Mittelwerts auch durch die Grenze des zentralen Theorems an die obige Normalverteilung angenähert werden.

Da die Stichprobenverteilung des Mittelwerts einer Normalverteilung folgt, lautet die Formel zur Berechnung aller Wahrscheinlichkeiten im Zusammenhang mit dem Stichprobenmittelwert :

Z=\cfrac{\overline{x}-\mu}{\displaystyle\frac{\sigma}{\sqrt{n}}}

Gold:

  • \overline{x}

    ist das Beispielmittel.

  • \mu

    Dies ist der Bevölkerungsdurchschnitt.

  • s

    ist die Populationsstandardabweichung.

  • n

    ist die Stichprobengröße.

  • Z

    ist eine durch die Standardnormalverteilung N(0,1) definierte Variable.

Stichprobenverteilung des Anteils

Wenn wir einen Teil einer Stichprobe untersuchen, analysieren wir tatsächlich Erfolgsfälle. Daher folgt die Zufallsvariable in der Studie einer binomialen Wahrscheinlichkeitsverteilung.

Nach dem zentralen Grenzwertsatz können wir für große Größen (n>30) eine Binomialverteilung näher an eine Normalverteilung bringen. Daher nähert sich die Stichprobenverteilung des Anteils einer Normalverteilung mit den folgenden Parametern an:

\begin{array}{c}\displaystyle\mu_{p}=p \qquad \sigma_{p}=\sqrt{\frac{pq}{n}}\\[4ex]\displaystyle N_{p}\left(p, \sqrt{\frac{pq}{n}}\right) \end{array}

Gold

p

ist die Erfolgswahrscheinlichkeit und

q

ist die Wahrscheinlichkeit des Scheiterns

q=1-p

.

Hinweis: Eine Binomialverteilung kann nur dann einer Normalverteilung angenähert werden, wenn

n>30″ title=“Rendered by QuickLaTeX.com“ height=“14″ width=“52″ style=“vertical-align: -2px;“></p> <p> ,</p> <p class=np\ge 5

Und

nq\ge 5

.

Da die Stichprobenverteilung des Anteils einer Normalverteilung angenähert werden kann, lautet die Formel zur Berechnung einer Wahrscheinlichkeit im Zusammenhang mit dem Anteil einer Stichprobe daher:

Z=\cfrac{\widehat{p}-p}{\displaystyle\sqrt{\frac{pq}{n}}}

Gold:

  • \widehat{p}

    ist der Stichprobenanteil.

  • p

    ist der Anteil der Bevölkerung.

  • q

    ist die Ausfallwahrscheinlichkeit der Bevölkerung,

    q=1-p

    .

  • n

    ist die Stichprobengröße.

  • Z

    ist eine durch die Standardnormalverteilung N(0,1) definierte Variable.

Stichprobenverteilung der Varianz

Die Stichprobenvarianzverteilung wird durch die Chi-Quadrat-Wahrscheinlichkeitsverteilung definiert. Daher lautet die Formel für die Statistik der Stichprobenvarianzverteilung :

\chi^2=\cfrac{(n-1)s^2}{\sigma^2}

Gold:

  • \chi^2

    ist die Statistik der Stichprobenvarianzverteilung, die einer Chi-Quadrat-Verteilung folgt.

  • n

    ist die Stichprobengröße.

  • s^2

    ist die Stichprobenvarianz.

  • \sigma^2

    ist die Populationsvarianz.

Stichprobenverteilung der Mittelwertdifferenz

Wenn die Stichprobengröße groß genug ist (n 1 ≥ 30 und n 2 ≥ 30), folgt die Stichprobenverteilung der Mittelwertdifferenz einer Normalverteilung. Genauer gesagt werden die Parameter dieser Verteilung wie folgt berechnet:

\begin{array}{c}\displaystyle \mu_{\overline{x_1}-\overline{x_2}}=\mu_1-\mu_2 \qquad \sigma_{\overline{x_1}-\overline{x_2}}=\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\\[6ex]\displaystyle N_{\overline{x_1}-\overline{x_2}}\left(\mu_1-\mu_2, \sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right) \end{array}

Hinweis: Wenn es sich bei beiden Grundgesamtheiten um Normalverteilungen handelt, folgt die Stichprobenverteilung der Mittelwertdifferenz unabhängig von der Stichprobengröße einer Normalverteilung.

Da die Stichprobenverteilung der Mittelwertdifferenz durch eine Normalverteilung definiert ist, lautet die Formel zur Berechnung der Statistik der Stichprobenverteilung der Mittelwertdifferenz daher:

Z=\cfrac{(\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}

Gold:

  • \overline{x_i}

    ist der Mittelwert der Stichprobe i.

  • \mu_i

    ist der Mittelwert der Bevölkerung i.

  • \sigma_i

    ist die Standardabweichung der Grundgesamtheit i.

  • n_i

    ist die Stichprobengröße i.

  • Z

    ist eine durch die Standardnormalverteilung N(0,1) definierte Variable.

Beachten Sie, dass Stichproben aus verschiedenen Populationen unterschiedliche Stichprobengrößen haben können.

Stichprobenverteilung der Differenz in den Proportionen

Die für die Stichprobenverteilung der unterschiedlichen Anteile ausgewählten Stichproben werden durch Binomialverteilungen definiert, da ein Anteil für praktische Zwecke ein Verhältnis von Erfolgsfällen zur Gesamtzahl der Beobachtungen ist.

Aufgrund des zentralen Grenzwertsatzes können Binomialverteilungen jedoch an normale Wahrscheinlichkeitsverteilungen angenähert werden. Daher kann die Stichprobenverteilung der Proportionsdifferenz einer Normalverteilung mit den folgenden Merkmalen angenähert werden:

\begin{array}{c}\displaystyle\mu_{\widehat{p_1}-\widehat{p_2}}=p_1-p_2 \qquad \sigma_{\widehat{p_1}-\widehat{p_2}}=\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\\[6ex]\displaystyle N_{p}\left(p_1-p_2, \sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\right) \end{array}

Hinweis: Die Stichprobenverteilung der Proportionsdifferenz kann nur dann einer Normalverteilung angenähert werden, wenn

n_1\geq30

,

n_2\geq 30

,

n_1p_1\geq5

,

n_2p_2\geq5

,

n_1q_1\geq5

Und

n_2q_2\geq5

.

Da die Stichprobenverteilung der Proportionsdifferenz einer Normalverteilung angenähert werden kann, lautet die Formel zur Berechnung der Statistik der Stichprobenverteilung der Proportionsdifferenz wie folgt:

Z=\cfrac{(\widehat{p_1}-\widehat{p_2})-(p_1-p_2)}{\displaystyle\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}}

Gold:

  • \widehat{p_i}

    ist der Stichprobenanteil i.

  • p_i

    ist der Anteil der Bevölkerung i.

  • q_i

    ist die Ausfallwahrscheinlichkeit der Population i,

    q_i=1-p_i

    .

  • n_i

    ist die Stichprobengröße i.

  • Z

    ist eine durch die Standardnormalverteilung N(0,1) definierte Variable.

Über den Autor

Benjamin Anderson
Dr. Benjamin Anderson

Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen

Einen Kommentar hinzufügen

Deine E-Mail-Adresse wird nicht veröffentlicht. Erforderliche Felder sind mit * markiert