Stichprobenverteilung der differenz in den proportionen

In diesem Artikel wird erläutert, was der Unterschied in der Stichprobenverteilung ist und wofür er in der Statistik verwendet wird. Außerdem werden die Formel für die unterschiedliche Proportionen der Stichprobenverteilung und eine Schritt-für-Schritt-Übung vorgestellt.

Wie ist die Stichprobenverteilung des Unterschieds in den Proportionen?

Die Stichprobenverteilung der Differenzanteile ist die Verteilung, die sich aus der Berechnung der Unterschiede zwischen den Stichprobenanteilen aller möglichen Stichproben aus zwei verschiedenen Grundgesamtheiten ergibt.

Das heißt, der Prozess zum Erhalten der Stichprobenverteilung der Differenz der Anteile besteht erstens darin, alle möglichen Stichproben aus zwei verschiedenen Populationen zu extrahieren, zweitens den Anteil jeder extrahierten Stichprobe zu bestimmen und schließlich die Differenz zwischen allen zu bestimmen Proportionen der Differenz der Proportionen. zwei Populationen. Damit bildet die nach Durchführung dieser Vorgänge erhaltene Ergebnismenge die Stichprobenverteilung der Proportionsdifferenz.

In der Statistik wird der Unterschied in den Proportionen der Stichprobenverteilung verwendet, um die Wahrscheinlichkeit zu berechnen, dass der Unterschied zwischen den Stichprobenanteilen zweier zufällig ausgewählter Stichproben nahe am Unterschied in den Bevölkerungsanteilen liegt.

Formel zur Stichprobenverteilung der Proportionsdifferenz

Die für die unterschiedliche Proportionsstichprobenverteilung ausgewählten Stichproben werden durch Binomialverteilungen definiert, da für praktische Zwecke ein Anteil ein Verhältnis erfolgreicher Fälle zur Gesamtzahl der Beobachtungen ist.

Dennoch können Binomialverteilungen aufgrund des zentralen Grenzwertsatzes an normale Wahrscheinlichkeitsverteilungen angenähert werden. Daher kann die Stichprobenverteilung der Proportionsdifferenz einer Normalverteilung mit den folgenden Merkmalen angenähert werden:

Hinweis: Die Stichprobenverteilung der Proportionsdifferenz kann nur dann einer Normalverteilung angenähert werden, wenn

,

,

,

,

Und

.

Da die Stichprobenverteilung der Proportionsdifferenz einer Normalverteilung angenähert werden kann, lautet die Formel zur Berechnung der Statistik der Stichprobenverteilung der Proportionsdifferenz wie folgt:

Gold:

• 

  ist der Stichprobenanteil i.

• 

  ist der Anteil der Bevölkerung i.

• 

  ist die Ausfallwahrscheinlichkeit der Population i,

  

  .

• 

  ist die Stichprobengröße i.

• 

  ist eine durch die Standardnormalverteilung N(0,1) definierte Variable.

Diese Formel ähnelt der Hypothesentestformel für Proportionsunterschiede.

Konkretes Beispiel für die Stichprobenverteilung unterschiedlicher Proportionen

Nachdem Sie die Definition der Proportionsdifferenz-Stichprobenverteilung und ihre Formel kennengelernt haben, können Sie unten ein Schritt-für-Schritt-Lösungsbeispiel sehen, um das Konzept vollständig zu verstehen.

• Sie möchten die Genauigkeit zweier Produktionsanlagen analysieren. Eine Fabrik produziert so, dass nur 5 % der produzierten Teile Mängel aufweisen, während in einer anderen Fabrik der Anteil fehlerhafter Teile bei 8 % liegt. Wenn wir eine Stichprobe von 200 Teilen aus der ersten Fabrik und eine weitere Stichprobe von 280 Teilen aus der zweiten Fabrik nehmen, wie hoch ist dann die Wahrscheinlichkeit, dass der Prozentsatz der Mängel im ersten Produktionswerk größer ist als der Prozentsatz der Mängel im zweiten Werk? Produktion?

Um alle Daten des Problems vollständig zu kennen, berechnen wir zunächst den Anteil gut produzierter Teile jeder Pflanze:

Wenn die Fehlerquote in der ersten Fabrik größer wäre als die Fehlerquote in der zweiten Fabrik, würde die folgende Gleichung gelten:

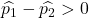
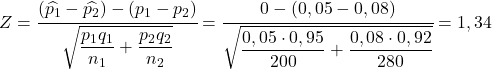
Somit entspricht die Wahrscheinlichkeit, dass die Fehlerquote der ersten Fabrik größer ist als die Fehlerquote der zweiten Fabrik, der Wahrscheinlichkeit, dass die Variable Z größer als 1,34 ist:

Normalverteilungstabelle suchen und schon haben wir das Problem gelöst:

➤ Siehe: Stichprobenverteilung der Mittelwertdifferenz