Stichprobenverteilung der mittelwertdifferenz

Von Dr. Benjamin Anderson August 3, 2023 Statistiken Keine Kommentare

In diesem Artikel wird erläutert, wie die Stichprobenverteilung der Differenz zwischen zwei Mittelwerten in der Statistik aussieht. Außerdem finden Sie die Formel zur Stichprobenverteilung der Mittelwertdifferenz und zusätzlich eine Schritt-für-Schritt-Lösung.

Wie ist die Stichprobenverteilung der Mittelwertdifferenz?

Die Stichprobenverteilung der Mittelwertdifferenz ist die Verteilung, die sich aus der Berechnung der Differenzen zwischen den Mittelwerten aller möglichen Stichproben aus zwei verschiedenen Grundgesamtheiten ergibt.

Das heißt, um die Stichprobenverteilung der Differenz der Mittelwerte zu erhalten, müssen alle möglichen Stichproben aus zwei Studienpopulationen ausgewählt werden, dann wird der Mittelwert jeder ausgewählten Stichprobe berechnet und schließlich wird die Differenz zwischen allen Mittelwerten aus den beiden Populationen berechnet. Somit bildet der nach Anwendung all dieser Operationen erhaltene Wertesatz die Stichprobenverteilung der Mittelwertdifferenz.

Die Differenz der Mittelwerte der Stichprobenverteilung wird verwendet, um die Wahrscheinlichkeit zu berechnen, dass die Differenz zwischen zwei Mittelwerten zufällig ausgewählter Stichproben aus zwei verschiedenen Grundgesamtheiten nahe an der Differenz der Mittelwerte der Grundgesamtheit liegt.

➤ Siehe: Stichprobenverteilung des Mittelwerts

Formel für die Stichprobenverteilung der Mittelwertdifferenz

Wenn die Stichprobengröße groß genug ist (n ₁ ≥ 30 und n ₂ ≥ 30), folgt die Stichprobenverteilung der Mittelwertdifferenz einer Normalverteilung. Genauer gesagt werden die Parameter dieser Verteilung wie folgt berechnet:

$\begin{array}{c}\displaystyle \mu_{\overline{x_1}-\overline{x_2}}=\mu_1-\mu_2 \qquad \sigma_{\overline{x_1}-\overline{x_2}}=\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\\[6ex]\displaystyle N_{\overline{x_1}-\overline{x_2}}\left(\mu_1-\mu_2, \sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right) \end{array}$

Hinweis: Wenn es sich bei beiden Grundgesamtheiten um Normalverteilungen handelt, folgt die Stichprobenverteilung der Mittelwertdifferenz unabhängig von der Stichprobengröße einer Normalverteilung.

Da die Stichprobenverteilung der Mittelwertdifferenz durch eine Normalverteilung definiert ist, lautet die Formel zur Berechnung der Statistik der Stichprobenverteilung der Mittelwertdifferenz daher:

$Z=\cfrac{(\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}$

Gold:

$\overline{x_i}$

ist der Mittelwert der Stichprobe i.
$\mu_i$

ist der Mittelwert der Bevölkerung i.
$\sigma_i$

ist die Standardabweichung der Grundgesamtheit i.
$n_i$

ist die Stichprobengröße i.
$Z$

ist eine durch die Standardnormalverteilung N(0,1) definierte Variable.

Beachten Sie, dass Stichproben aus verschiedenen Populationen unterschiedliche Stichprobengrößen haben können.

Konkretes Beispiel für die Stichprobenverteilung der Mittelwertdifferenz

Sobald wir die Definition der Differenz der Mittelwert-Stichprobenverteilung und ihre Formel gesehen haben, sehen wir uns ein Schritt-für-Schritt-Beispiel an, um das Konzept der Differenz der Mittelwert-Stichprobenverteilung vollständig zu verstehen.

In einer statistischen Studie wollen wir den Unterschied zwischen der Körpergröße von Jungen und Mädchen eines bestimmten Alters analysieren. Wir wissen, dass die Verteilung, die die Population der Jungen dieses Alters definiert, einen Mittelwert von 157 cm und eine Standardabweichung von 9 cm aufweist, und dass andererseits die Verteilung, die die Population der Mädchen dieses Alters definiert, einen Mittelwert von 148 hat cm und einer Standardabweichung von 7 cm. Wenn eine Stichprobe von 30 Jungen dieses Alters und eine Stichprobe von 35 Mädchen dieses Alters ausgewählt werden, wie groß ist die Wahrscheinlichkeit, dass die durchschnittliche Größe der Stichprobe der Jungen 12 cm größer ist als die durchschnittliche Größe der Stichprobe der Mädchen?

Um dieses Problem zu lösen, muss zunächst die Statistik der Differenz der mittleren Stichprobenverteilung berechnet werden. Wir wenden daher die oben gezeigte Formel an:

$Z=\cfrac{(\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right)}=\cfrac{12-(157-148)}{\displaystyle\sqrt{\frac{9^2}{30}+\frac{7^2}{35}}}=1,48$

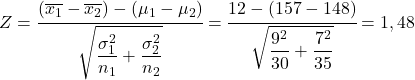
Daher entspricht die Wahrscheinlichkeit, dass die durchschnittliche Stichprobengröße von Jungen 12 cm größer ist als die durchschnittliche Größe von Mädchen, der Wahrscheinlichkeit, dass die Z-Variable größer als 1,48 ist.

$P[(\overline{x_1}-\overline{x_2})>12]=P[Z>1,48]“ title=“Rendered by QuickLaTeX.com“ height=“19″ width=“253″ style=“vertical-align: -5px;“></p> </p> <p> Wir suchen daher in der <a href=$ Tabelle von Z nach der Wahrscheinlichkeit von Z>1,48:

$P[(\overline{x_1}-\overline{x_2})>12]=P[Z>1,48]=0,0694″ title=“Rendered by QuickLaTeX.com“ height=“19″ width=“331″ style=“vertical-align: -5px;“></p> </p> <p> Kurz gesagt beträgt die Wahrscheinlichkeit, dass die durchschnittliche Stichprobengröße von Jungen 12 cm größer ist als die durchschnittliche Größe von Mädchen, 6,94 %.</p> </div>  <div class=$

Über den Autor

Dr. Benjamin Anderson

Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen

Wie ist die Stichprobenverteilung der Mittelwertdifferenz?

Formel für die Stichprobenverteilung der Mittelwertdifferenz

Konkretes Beispiel für die Stichprobenverteilung der Mittelwertdifferenz

Über den Autor

Dr. Benjamin Anderson

Einen Kommentar hinzufügen