Stichprobenverteilung des mittelwerts

In diesem Artikel wird erläutert, wie die Stichprobenverteilung des Mittelwerts in der Statistik aussieht. Außerdem finden Sie die Formel für die mittlere Stichprobenverteilung und eine Schritt-für-Schritt-Lösung für die Übung.

Wie ist die Stichprobenverteilung des Mittelwerts?

Die Stichprobenverteilung des Mittelwerts (oder Stichprobenverteilung der Mittelwerte ) ist die Verteilung, die sich aus der Berechnung des Stichprobenmittelwerts jeder möglichen Stichprobe aus einer Grundgesamtheit ergibt. Das heißt, die Menge der Stichprobenmittelwerte aller möglichen Stichproben einer Grundgesamtheit bildet die Stichprobenverteilung des Mittelwerts.

Mit anderen Worten: Wenn wir alle Stichproben untersuchen, die einer Grundgesamtheit entnommen werden können, und den Durchschnitt jeder Stichprobe berechnen, bildet die Menge der berechneten Werte eine Stichprobenverteilung des Stichprobenmittelwerts.

In der Statistik wird die Stichprobenverteilung des Mittelwerts verwendet, um die Wahrscheinlichkeit zu berechnen, dass man sich bei der Analyse einer einzelnen Stichprobe dem Wert des Grundgesamtheitsmittelwerts annähert.

Formel für die Stichprobenverteilung des Mittelwerts

Gegeben sei eine Grundgesamtheit, die einer normalen Wahrscheinlichkeitsverteilung mit Mittelwert folgt

und Standardabweichung

und Größenproben werden extrahiert

, wird die Stichprobenverteilung des Mittelwerts auch durch eine Normalverteilung mit den folgenden Merkmalen definiert:

Gold

ist der Mittelwert der Stichprobenverteilung des Mittelwerts und

ist seine Standardabweichung. Außerdem,

ist der Standardfehler der Stichprobenverteilung.

Hinweis: Wenn die Grundgesamtheit keiner Normalverteilung folgt, aber die Stichprobengröße groß ist (n>30), kann die Stichprobenverteilung des Mittelwerts auch durch den zentralen Grenzwertsatz an die vorherige Normalverteilung angenähert werden.

Da die Stichprobenverteilung des Mittelwerts einer Normalverteilung folgt, lautet die Formel zur Berechnung aller Wahrscheinlichkeiten im Zusammenhang mit dem Stichprobenmittelwert :

Gold:

• 

  ist das Beispielmittel.

• 

  Dies ist der Bevölkerungsdurchschnitt.

• 

  ist die Populationsstandardabweichung.

• 

  ist die Stichprobengröße.

• 

  ist eine durch die Standardnormalverteilung N(0,1) definierte Variable.

Praxisbeispiel für die Stichprobenverteilung des Mittelwerts

Nachdem wir die Definition der Stichprobenverteilung des Mittelwerts und die damit verbundenen Formeln kennengelernt haben, lösen wir ein Beispiel, um das Konzept besser zu verstehen.

• Das Gewicht der Universitätsstudenten folgt einer Normalverteilung mit einem Mittelwert von 68 kg und einer Standardabweichung von 9 kg. Bestimmt:
  1. Wie groß ist die Wahrscheinlichkeit, dass der Durchschnitt einer Zufallsstichprobe von 25 Schülern weniger als 66 kg wiegt?
  2. Wenn 300 Proben mit einer Größe von jeweils 25 Schülern entnommen werden, wie viele Probenmittelwerte haben dann einen Wert von weniger als 66 kg?

Zunächst müssen wir den Wert der entsprechenden Statistik berechnen. Dazu wenden wir die Formel an, die wir oben gesehen haben:

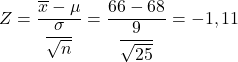
Die gesuchte Wahrscheinlichkeit entspricht daher dem Wert Z=-1,11 des linken Endes der Standardnormalverteilung, der leicht aus der Z-Wahrscheinlichkeitstabelle ermittelt werden kann. Wir verwenden daher die Z-Tabelle, um die Wahrscheinlichkeit zu bestimmen, mit der das Problem uns fragt:

Nachdem wir nun die Wahrscheinlichkeit kennen, dass der Mittelwert einer Zufallsprobe weniger als 66 kg beträgt, müssen wir die berechnete Wahrscheinlichkeit mit der Gesamtzahl der entnommenen Proben multiplizieren, um zu wissen, wie viele Proben bei 300 gleichen Proben weniger als 66 kg betragen:

Daher werden etwa 40 der entnommenen Proben im Durchschnitt weniger als 66 kg wiegen.