So berechnen sie stichprobenverteilungen in excel

Eine Stichprobenverteilung ist eine Wahrscheinlichkeitsverteilung einer bestimmten Statistik , die auf vielen Zufallsstichproben aus einer einzelnen Grundgesamtheit basiert.

In diesem Tutorial wird erläutert, wie Sie mit Stichprobenverteilungen in Excel Folgendes tun:

• Generieren Sie eine Stichprobenverteilung.
• Visualisieren Sie die Stichprobenverteilung.
• Berechnen Sie den Mittelwert und die Standardabweichung der Stichprobenverteilung.
• Berechnen Sie die Wahrscheinlichkeiten bezüglich der Stichprobenverteilung.

Generieren Sie eine Stichprobenverteilung in Excel

Angenommen, wir möchten eine Stichprobenverteilung generieren, die aus 1.000 Stichproben besteht, wobei jede Stichprobengröße 20 beträgt und aus einer Normalverteilung mit einem Mittelwert von 5,3 und einer Standardabweichung von 9 stammt.

Wir können dies ganz einfach tun, indem wir die folgende Formel in Zelle A2 unserer Tabelle eingeben:

 = NORM . INV ( RAND (), 5.3, 9)

Wir können dann mit der Maus über die rechte untere Ecke der Zelle fahren, bis ein kleines + erscheint, und die Formel 20 Zellen nach rechts und 1000 Zellen nach unten ziehen:

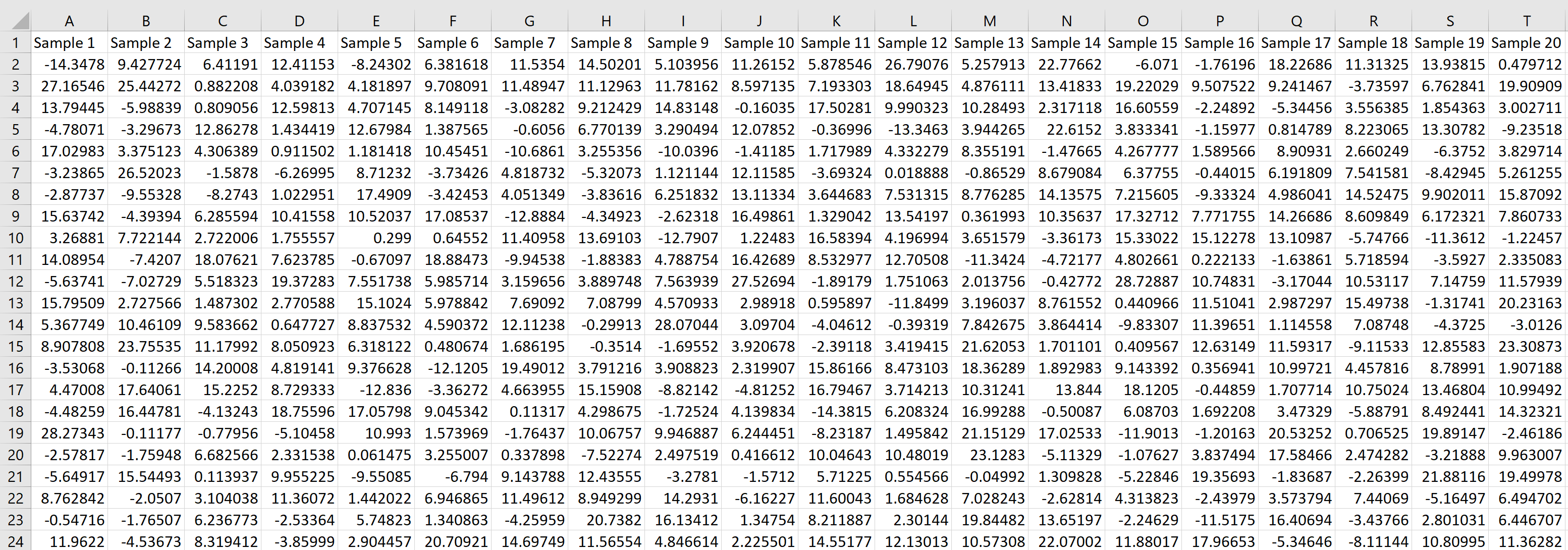
Jede Zeile stellt eine Stichprobe der Größe 20 dar, in der jeder Wert aus einer Normalverteilung mit einem Mittelwert von 5,3 und einer Standardabweichung von 9 stammt.

Ermitteln Sie den Mittelwert und die Standardabweichung

Um den Mittelwert und die Standardabweichung dieser Stichprobenverteilung der Stichprobenmittelwerte zu ermitteln, können wir zunächst den Mittelwert jeder Stichprobe ermitteln, indem wir die folgende Formel in Zelle U2 unseres Arbeitsblatts eingeben:

 = AVERAGE (A2:T2)

Wir können dann mit der Maus über die rechte untere Ecke der Zelle fahren, bis ein kleines + erscheint, und doppelklicken, um diese Formel in alle anderen Zellen in Spalte U zu kopieren:

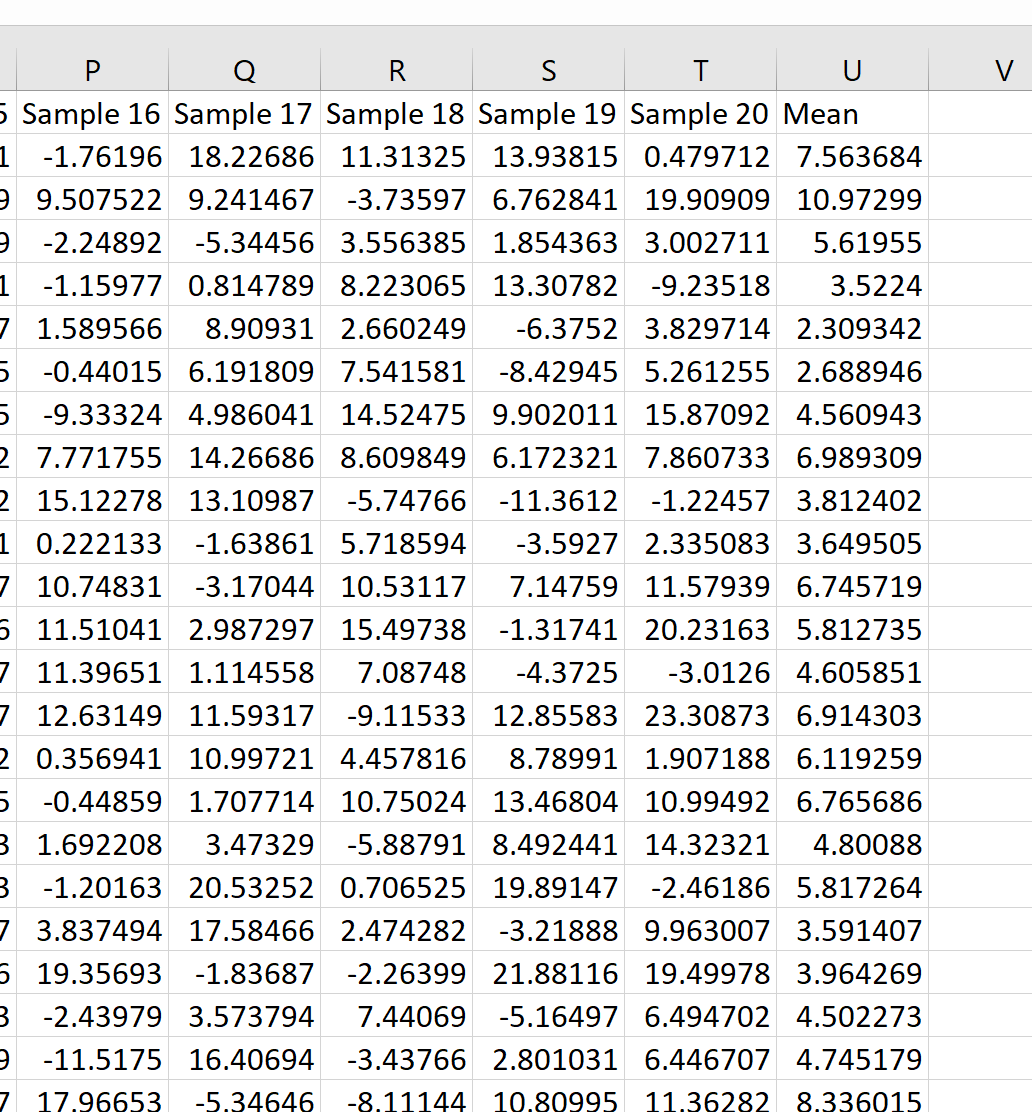
Wir können sehen, dass die erste Stichprobe einen Mittelwert von 7,563684 hatte, die zweite Stichprobe einen Mittelwert von 10,97299 und so weiter.

Anschließend können wir die folgenden Formeln verwenden, um den Mittelwert und die Standardabweichung der Stichprobenmittelwerte zu berechnen:

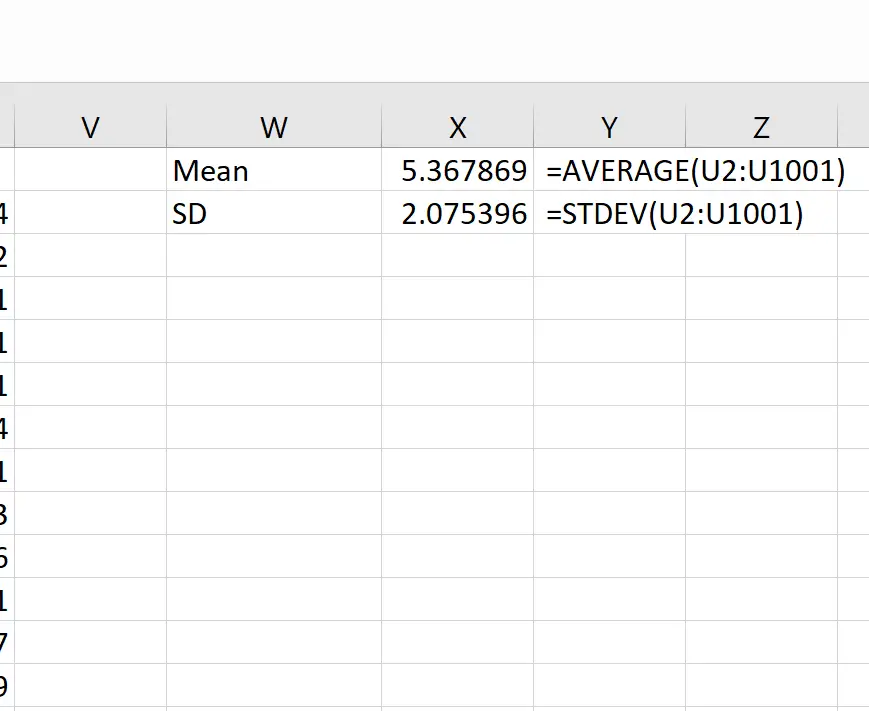
Theoretisch sollte der Mittelwert der Stichprobenverteilung 5,3 betragen. Wir können sehen, dass der tatsächliche Stichprobenmittelwert in diesem Beispiel 5,367869 ist, was nahe bei 5,3 liegt.

Und theoretisch sollte die Standardabweichung der Stichprobenverteilung gleich s/√n sein, was 9 / √20 = 2,012 wäre. Wir können sehen, dass die tatsächliche Standardabweichung der Stichprobenverteilung 2,075396 beträgt, was nahe bei 2,012 liegt.

Visualisieren Sie die Stichprobenverteilung

Wir können auch ein einfaches Histogramm erstellen, um die Stichprobenverteilung der Stichprobenmittelwerte zu visualisieren.

Markieren Sie dazu einfach alle Stichprobenmittelwerte in Spalte U, klicken Sie auf die Registerkarte „Einfügen “ und dann auf die Option „Histogramm“ im Abschnitt „Diagramme “.

Dies ergibt das folgende Histogramm:

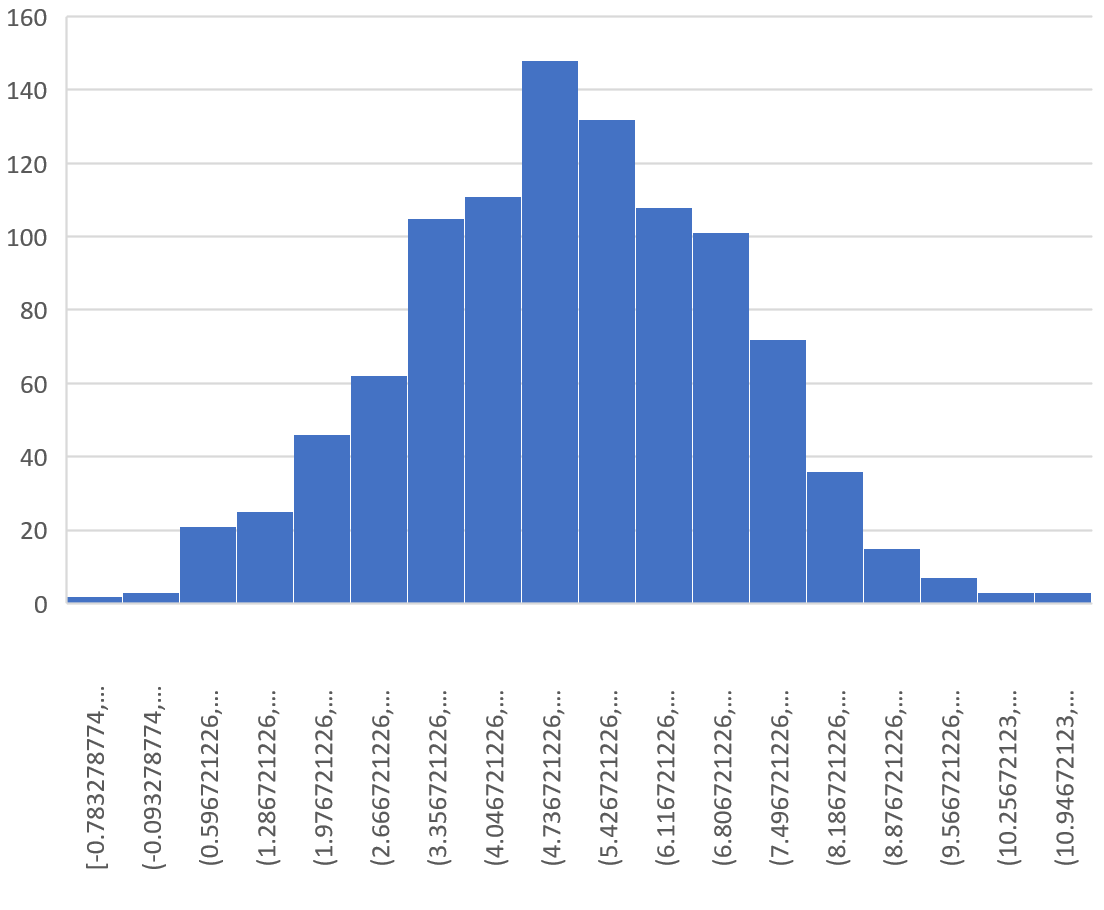
Es ist zu erkennen, dass die Stichprobenverteilung glockenförmig ist mit einem Peak nahe dem Wert 5.

Aus den Enden der Verteilung können wir jedoch erkennen, dass einige Stichproben Mittelwerte größer als 10 und andere Mittelwerte kleiner als 0 hatten.

Berechnen Sie die Wahrscheinlichkeiten

Wir können auch die Wahrscheinlichkeit berechnen, einen bestimmten Wert für einen Stichprobenmittelwert zu erhalten, basierend auf dem Grundgesamtheitsmittelwert, der Grundgesamtheitsstandardabweichung und der Stichprobengröße.

Beispielsweise können wir die folgende Formel verwenden, um die Wahrscheinlichkeit zu ermitteln, dass der Stichprobenmittelwert kleiner oder gleich 6 ist, vorausgesetzt, der Grundgesamtheitsmittelwert beträgt 5,3, die Grundgesamtheitsstandardabweichung beträgt 9 und die Stichprobengröße beträgt:

 = COUNTIF (U2:U1001, " <=6 ")/ COUNT (U2:U1001)

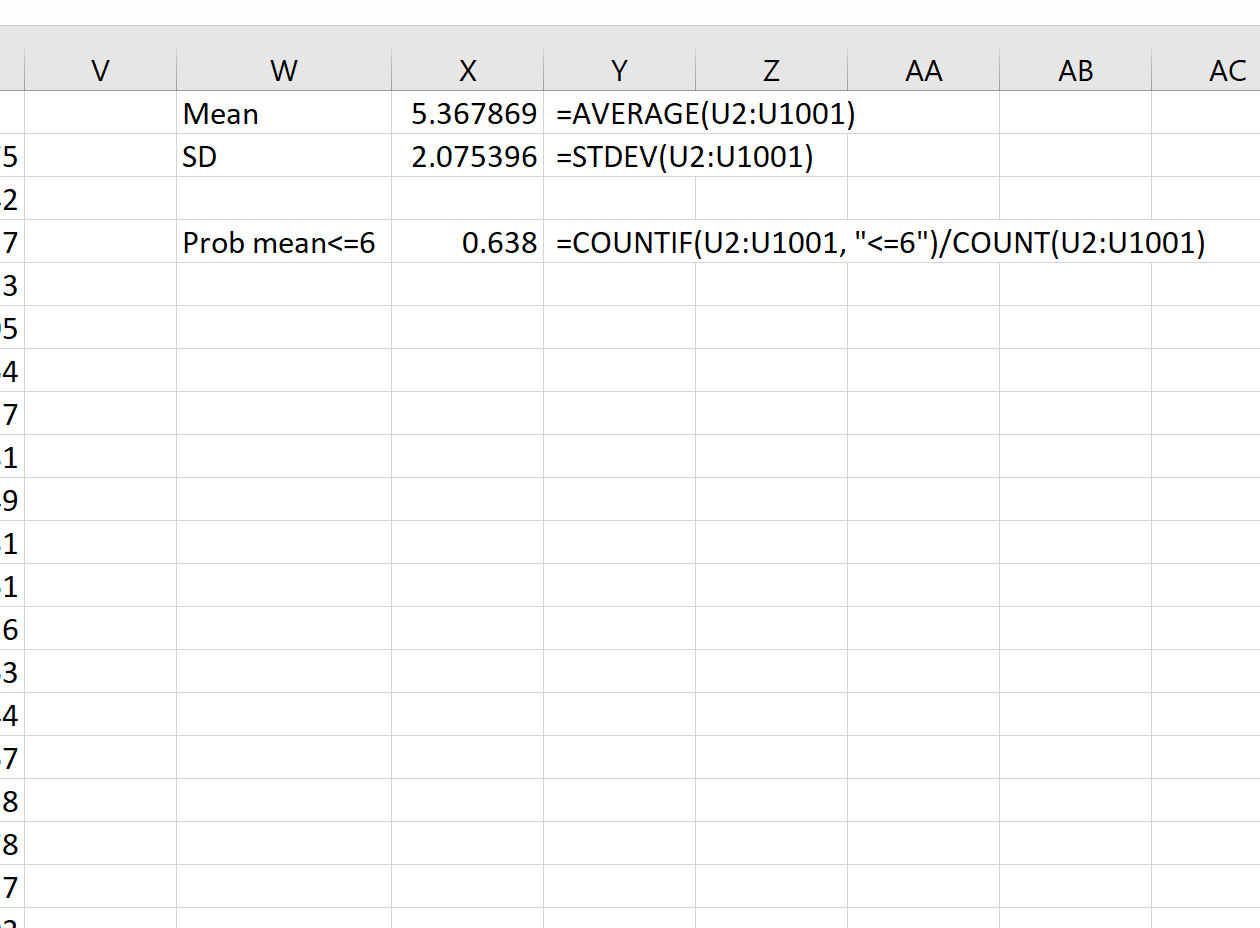
Wir sehen, dass die Wahrscheinlichkeit, dass der Stichprobenmittelwert kleiner oder gleich 6 ist, 0,638 beträgt.

Dies kommt der vom Stichprobenverteilungsrechner berechneten Wahrscheinlichkeit sehr nahe:

Zusätzliche Ressourcen

Eine Einführung in Stichprobenverteilungen
Stichprobenverteilungsrechner
Eine Einführung in den zentralen Grenzwertsatz