So berechnen sie stichprobenverteilungen in r

Eine Stichprobenverteilung ist eine Wahrscheinlichkeitsverteilung einer bestimmten Statistik basierend auf vielen Zufallsstichproben aus einer einzelnen Grundgesamtheit.

In diesem Tutorial wird erklärt, wie Sie mit Stichprobenverteilungen in R Folgendes tun:

• Generieren Sie eine Stichprobenverteilung.
• Visualisieren Sie die Stichprobenverteilung.
• Berechnen Sie den Mittelwert und die Standardabweichung der Stichprobenverteilung.
• Berechnen Sie die Wahrscheinlichkeiten bezüglich der Stichprobenverteilung.

Generieren Sie eine Stichprobenverteilung in R

Der folgende Code zeigt, wie eine Stichprobenverteilung in R generiert wird:

 #make this example reproducible
set.seed(0)

#define number of samples
n = 10000

#create empty vector of length n
sample_means = rep (NA, n)

#fill empty vector with means
for (i in 1:n){
  sample_means[i] = mean ( rnorm (20, mean=5.3, sd=9))
}

#view first six sample means
head(sample_means)

[1] 5.283992 6.304845 4.259583 3.915274 7.756386 4.532656

In diesem Beispiel haben wir die Funktion rnorm() verwendet, um den Durchschnitt von 10.000 Stichproben zu berechnen, bei denen jede Stichprobengröße 20 betrug und aus einer Normalverteilung mit einem Mittelwert von 5,3 und einer Standardabweichung von 9 generiert wurde.

Wir können sehen, dass die erste Stichprobe einen Mittelwert von 5,283992 hatte, die zweite Stichprobe einen Mittelwert von 6,304845 und so weiter.

Visualisieren Sie die Stichprobenverteilung

Der folgende Code zeigt, wie man ein einfaches Histogramm zur Visualisierung der Stichprobenverteilung erstellt:

 #create histogram to visualize the sampling distribution
hist(sample_means, main = "", xlab = " Sample Means ", col = " steelblue ")

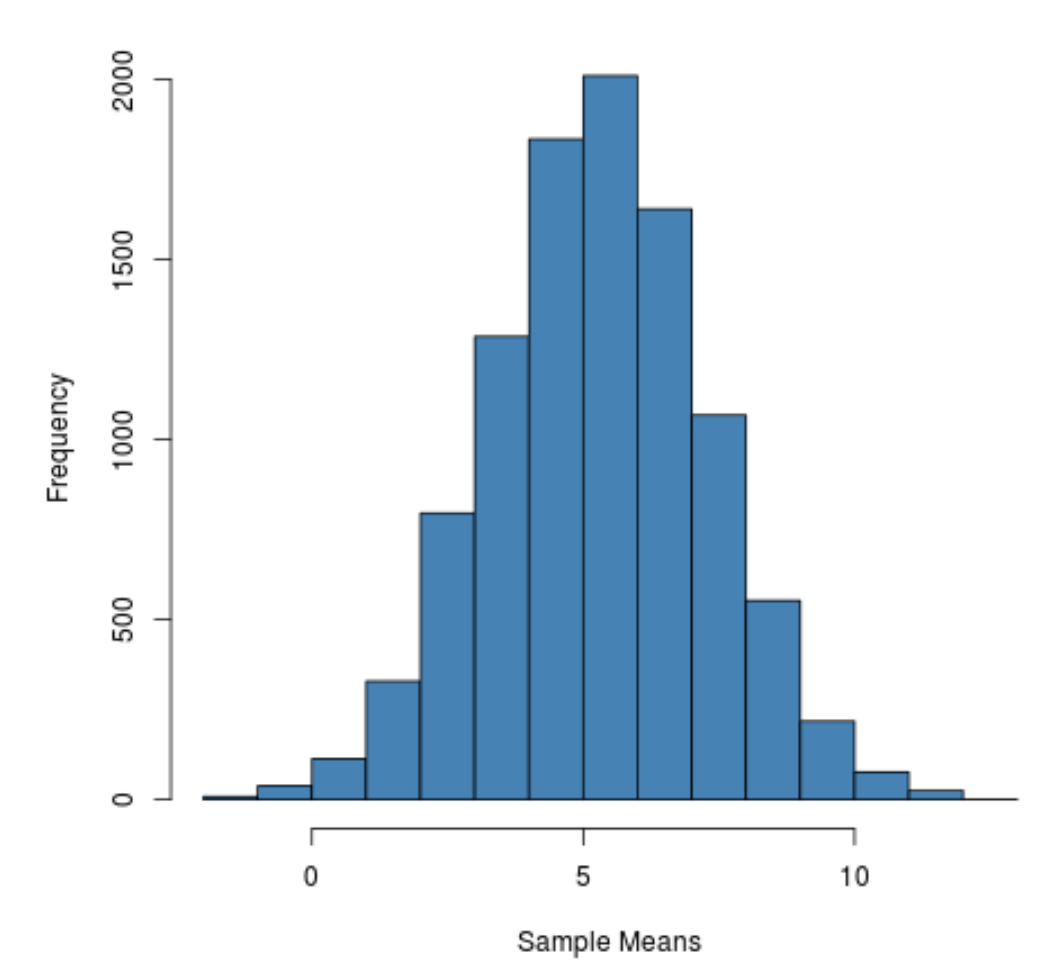
Es ist zu erkennen, dass die Stichprobenverteilung glockenförmig ist mit einem Peak nahe dem Wert 5.

Aus den Enden der Verteilung können wir jedoch erkennen, dass einige Stichproben Mittelwerte größer als 10 und andere Mittelwerte kleiner als 0 hatten.

Ermitteln Sie den Mittelwert und die Standardabweichung

Der folgende Code zeigt, wie der Mittelwert und die Standardabweichung der Stichprobenverteilung berechnet werden:

 #mean of sampling distribution
mean(sample_means)

[1] 5.287195

#standard deviation of sampling distribution
sd(sample_means)

[1] 2.00224

Theoretisch sollte der Mittelwert der Stichprobenverteilung 5,3 betragen. Wir können sehen, dass der tatsächliche Stichprobenmittelwert in diesem Beispiel 5,287195 ist, was nahe bei 5,3 liegt.

Und theoretisch sollte die Standardabweichung der Stichprobenverteilung gleich s/√n sein, was 9 / √20 = 2,012 wäre. Wir können sehen, dass die tatsächliche Standardabweichung der Stichprobenverteilung 2,00224 beträgt, was nahe bei 2,012 liegt.

Berechnen Sie die Wahrscheinlichkeiten

Der folgende Code zeigt, wie die Wahrscheinlichkeit berechnet wird, einen bestimmten Wert für einen Stichprobenmittelwert zu erhalten, wenn ein Grundgesamtheitsmittelwert, die Grundgesamtheitsstandardabweichung und die Stichprobengröße gegeben sind.

 #calculate probability that sample mean is less than or equal to 6
sum(sample_means <= 6) / length(sample_means)

In diesem speziellen Beispiel ermitteln wir die Wahrscheinlichkeit, dass der Stichprobenmittelwert kleiner oder gleich 6 ist, vorausgesetzt, dass der Grundgesamtheitsmittelwert 5,3 beträgt, die Grundgesamtheitsstandardabweichung 9 beträgt und die Stichprobengröße von 20 0,6417 beträgt.

Dies kommt der vom Stichprobenverteilungsrechner berechneten Wahrscheinlichkeit sehr nahe:

Der vollständige Code

Der vollständige R-Code, der in diesem Beispiel verwendet wird, ist unten dargestellt:

 #make this example reproducible
set.seed(0)

#define number of samples
n = 10000

#create empty vector of length n
sample_means = rep (NA, n)

#fill empty vector with means
for (i in 1:n){
  sample_means[i] = mean ( rnorm (20, mean=5.3, sd=9))
}

#view first six sample means
head(sample_means)

#create histogram to visualize the sampling distribution
hist(sample_means, main = "", xlab = " Sample Means ", col = " steelblue ")

#mean of sampling distribution
mean(sample_means)

#standard deviation of sampling distribution
sd(sample_means)

#calculate probability that sample mean is less than or equal to 6
sum(sample_means <= 6) / length(sample_means)

Zusätzliche Ressourcen

Eine Einführung in Stichprobenverteilungen
Stichprobenverteilungsrechner
Eine Einführung in den zentralen Grenzwertsatz