Streudiagramm
In diesem Artikel wird erklärt, was Streudiagramme sind. Sie erfahren daher, wofür eine Punktwolke verwendet wird, wie man eine Punktwolke erstellt, wie man sie interpretiert und Beispiele für Punktwolken.
Was ist eine Punktwolke?
Streudiagramm oder Streudiagramm ist eine Art statistisches Diagramm, in dem ein Datensatz aus zwei Variablen auf zwei kartesischen Koordinatenachsen grafisch dargestellt wird.
Daher werden Streudiagramme verwendet, um die Beziehung zwischen zwei statistischen Variablen zu analysieren.
Streudiagramme haben verschiedene Namen, beispielsweise Korrelationsdiagramm oder Streudiagramm .
Es ist zu beachten, dass das Streudiagramm ebenso wie das Pareto-Diagramm, das Ursache-Wirkungs-Diagramm, das Flussdiagramm usw. als eines der grundlegenden Werkzeuge der Qualitätskontrolle gilt.
So erstellen Sie ein Streudiagramm
Um ein Streudiagramm zu erstellen, müssen Sie die folgenden Schritte ausführen:
- Sammeln Sie statistische Daten von der Probe, die Sie analysieren möchten. Beachten Sie, dass zum Erstellen eines Streudiagramms mindestens zwei quantitative Variablen vorhanden sein müssen.
- Zeichnen Sie die beiden Achsen des Streudiagramms.
- Bestimmen Sie die beiden statistischen Variablen, die grafisch dargestellt werden.
- Kalibrieren Sie den Maßstab jeder Achse des Diagramms. Hierzu wird empfohlen, zunächst das Minimum und Maximum jeder Variablen zu ermitteln und anhand dieser Werte jede Achse zu skalieren.
- Stellen Sie jedes Datenpaar im Streudiagramm mit einem Punkt dar.
- Analysieren und interpretieren Sie das erhaltene Streudiagramm.
Beispiel für ein Streudiagramm
Nachdem wir die Definition eines Streudiagramms und die Theorie zu seiner Entstehung kennengelernt haben, wird in diesem Abschnitt ein Diagramm dieses Typs als Beispiel vorgestellt.
- In der folgenden Häufigkeitstabelle wurden die Mathematik- und Statistikergebnisse einer Stichprobe von 20 Schülern als Daten erfasst. Stellen Sie den Datensatz in einem Streudiagramm dar und analysieren Sie ihn.
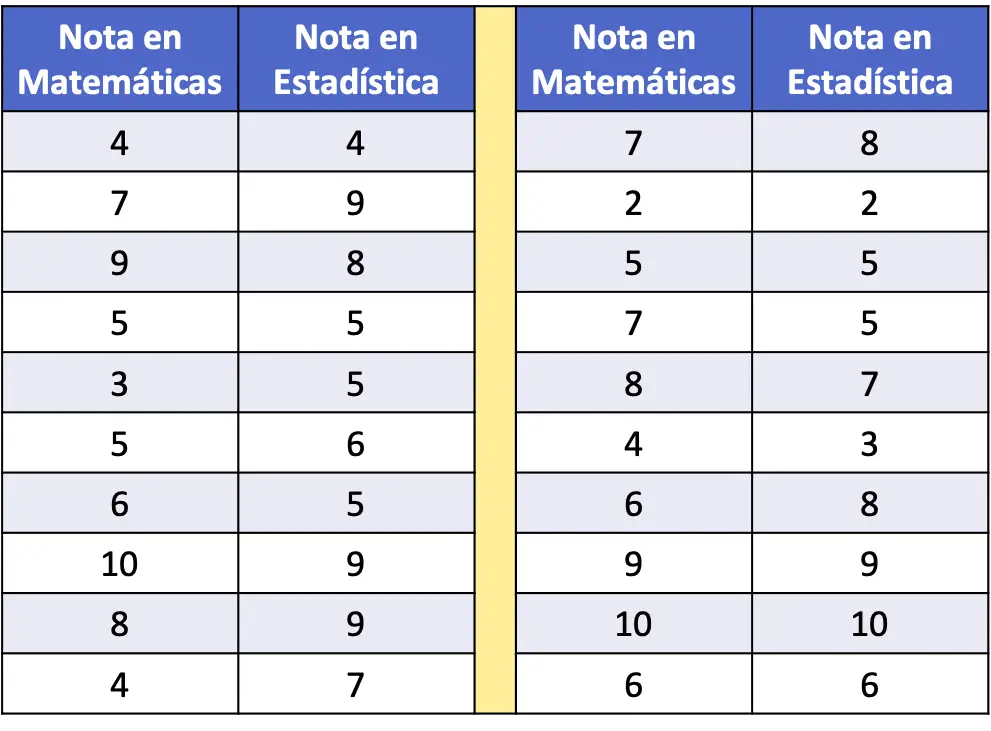
Um die Datenreihe in einem Streudiagramm darzustellen, müssen wir lediglich zwei Achsen zeichnen, sie kalibrieren und für jedes Datenpaar einen Punkt im Diagramm zeichnen. Denken Sie daran, dass ein Punkt in einem Diagramm am Schnittpunkt der imaginären Linien liegt, die jedem seiner Werte entsprechen.
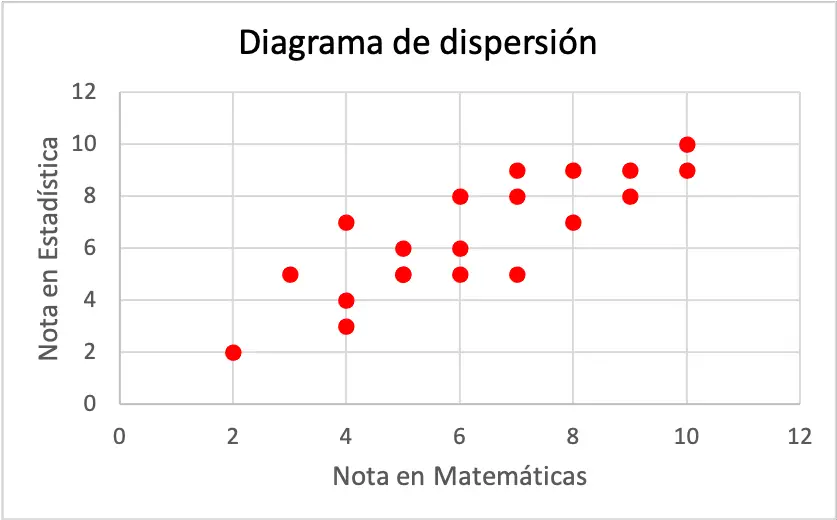
Jede Achse des Streudiagramms stellt eine Variable dar. Genauer gesagt entspricht die horizontale Achse der Note in Mathematik und die vertikale Achse hingegen der Note in Statistik.
Wie Sie dem Streudiagramm entnehmen können, besteht zwischen den beiden Variablen eine positive Korrelation, da eine Variable zunimmt, wenn auch die andere Variable zunimmt. Daraus lässt sich schließen, dass ein Schüler, der eine bessere Note in Mathematik erhält, mit größerer Wahrscheinlichkeit auch eine bessere Note in Statistik bekommt und umgekehrt.
Die bisherige Schlussfolgerung bedeutet jedoch nicht, dass eine Variable die Ursache für die andere ist, denn eine gute Note in Mathematik garantiert nicht automatisch eine gute Note in Statistik, ohne dass man etwas tun muss, sondern man sollte vielmehr beide Fächer studieren. Im nächsten Abschnitt gehen wir näher auf dieses Konzept ein.
Das Streudiagramm und die Korrelation
Anhand eines Streudiagramms lässt sich die Art der Korrelation zwischen zwei Variablen erkennen:
- Direkte Korrelation (oder positive Korrelation) : Eine Variable nimmt zu, wenn auch die andere zunimmt.
- Inverse Korrelation (oder negative Korrelation) : Wenn eine Variable zunimmt, nimmt die andere ab, und umgekehrt, wenn eine Variable abnimmt, nimmt die andere zu.
- Nullkorrelation (Keine Korrelation) : Es besteht keine Beziehung zwischen den beiden Variablen.
Unabhängig davon, ob die Korrelation zwischen den beiden Variablen direkt oder invers ist, kann die Korrelation auch basierend auf der Stärke oder Schwäche der Beziehung zwischen den beiden Variablen klassifiziert werden.
- Starke Korrelation: Die beiden Variablen sind eng miteinander verknüpft. Die Punkte werden in der Punktwolke zusammengeführt. Dies erleichtert die Identifizierung der Beziehung zwischen Variablen.
- Geringe Korrelation : Zwischen den beiden Variablen besteht eine Beziehung, die jedoch schwer zu erkennen ist. Die Punkte sind in der Punktwolke weit voneinander entfernt.

Andererseits kann die Korrelation auch numerisch mithilfe einer Formel berechnet werden, sodass Sie mathematisch wissen können, wie eng zwei verschiedene Variablen miteinander verbunden sind. Um zu sehen, wie es funktioniert, klicken Sie auf den folgenden Link:
Bedenken Sie, dass selbst wenn eine Korrelation zwischen zwei Variablen besteht, dies nicht bedeutet, dass zwischen ihnen eine Kausalität besteht, d. h. die Korrelation zwischen zwei Variablen bedeutet nicht, dass die Änderung in einer Variablen die Ursache für die Änderung in der anderen ist. Variable.
Wie im Streudiagramm im vorherigen Abschnitt besteht zwar ein positiver Zusammenhang zwischen der Note in Mathematik und der Note in Statistik, eine gute Note in Mathematik bedeutet jedoch nicht, dass man auch in Statistik eine gute Note erhält, denn wenn man nur Mathematik studiert, wird man mit Sicherheit scheitern in der Statistik. Daher hängen die beiden Variablen zusammen, sind aber nicht Ursache und Wirkung.
Um mehr zu erfahren, können Sie mit dem folgenden Beitrag fortfahren:
Vor- und Nachteile der Punktwolke
Aufgrund der Eigenschaften des Streudiagramms hat diese Art von statistischem Diagramm Vor- und Nachteile.
Vorteil:
- Es ist ganz einfach, eine Reihe von Daten in einem Streudiagramm darzustellen.
- Mit dem Streudiagramm können Sie die Beziehung zwischen zwei Variablen visuell analysieren und so leichter Schlussfolgerungen ziehen.
- Streudiagramme können auch in einer eingehenden statistischen Studie als vorläufige Datenexploration verwendet werden.
Nachteile:
- Diese Art von Diagrammen eignet sich nicht zur Darstellung qualitativer Variablen.
- Die Interpretation eines Streudiagramms kann zu einer falschen Schlussfolgerung über Ursache und Wirkung zwischen zwei Variablen führen.
- Mit Streudiagrammen können Sie die Beziehung zwischen mehr als zwei Variablen nicht analysieren.