So führen sie eine stückweise regression in r durch (schritt für schritt)

Die stückweise Regression ist eine Regressionsmethode, die wir häufig verwenden, wenn es in einem Datensatz klare „Haltepunkte“ gibt.

Das folgende Schritt-für-Schritt-Beispiel zeigt, wie man eine stückweise Regression in R durchführt.

Schritt 1: Erstellen Sie die Daten

Erstellen wir zunächst den folgenden Datenrahmen:

 #view DataFrame
df <- data. frame (x=c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16),
                 y=c(2, 4, 5, 6, 8, 10, 12, 13, 15, 19, 24, 28, 31, 34, 39, 44))

#view first six rows of data frame
head(df)

  xy
1 1 2
2 2 4
3 3 5
4 4 6
5 5 8
6 6 10

Schritt 2: Visualisieren Sie die Daten

Als Nächstes erstellen wir ein Streudiagramm zur Visualisierung der Daten:

 #create scatterplot of x vs. y
plot(df$x, df$y, pch= 16 , col=' steelblue ')

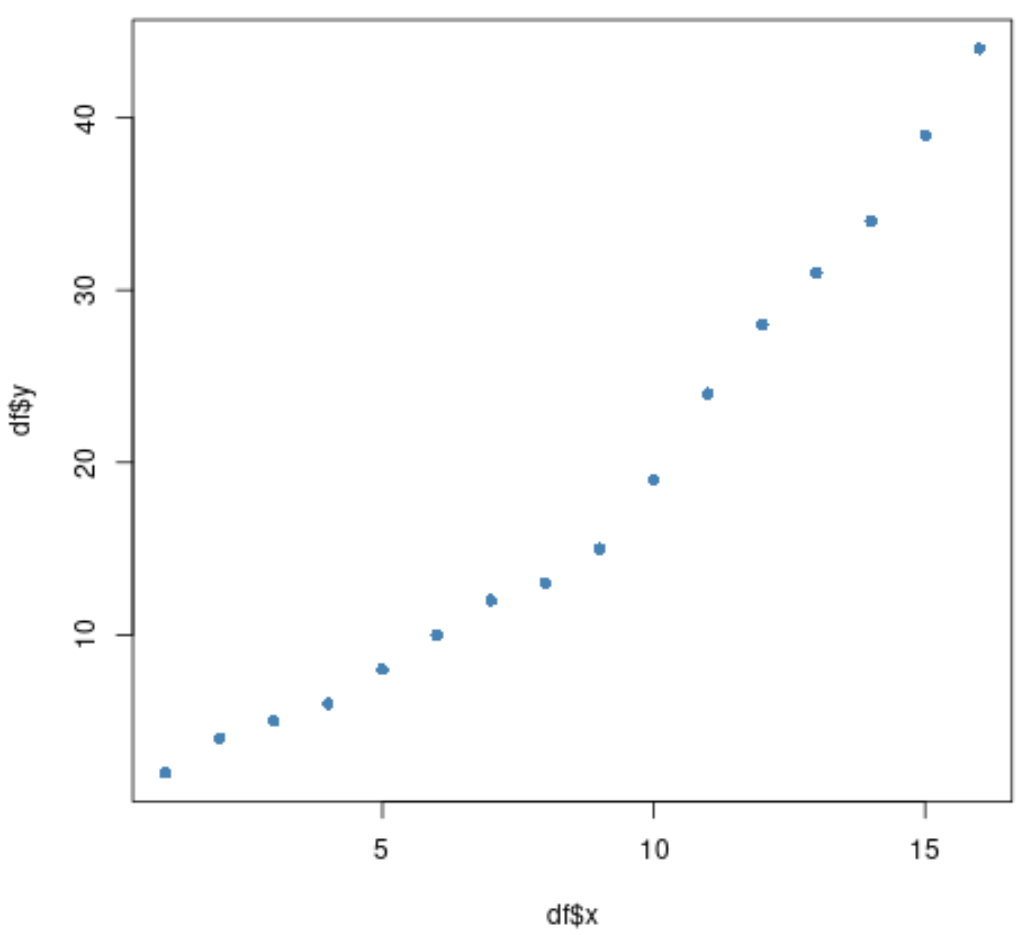
Wir können sehen, dass sich die Beziehung zwischen x und y um x = 9 herum abrupt zu ändern scheint.

Schritt 3: Passen Sie das stückweise Regressionsmodell an

Wir können die Funktion segmented() aus dem Segmented- Paket in R verwenden, um ein stückweises Regressionsmodell an unseren Datensatz anzupassen:

 library (segmented)

#fit simple linear regression model
fit <- lm(y ~ x, data=df)

#fit piecewise regression model to original model, estimating a breakpoint at x=9
segmented. fit <- segmented(fit, seg.Z = ~x, psi= 9 )

#view summary of segmented model
summary( segmented.fit )

Call: 
segmented.lm(obj = fit, seg.Z = ~x, psi = 9)

Estimated Break-Point(s):
         East. St.Err
psi1.x 8.762 0.26

Meaningful coefficients of the linear terms:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 0.32143 0.48343 0.665 0.519    
x 1.59524 0.09573 16.663 1.16e-09 ***
U1.x 2.40476 0.13539 17.762 NA    
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.6204 on 12 degrees of freedom
Multiple R-Squared: 0.9983, Adjusted R-squared: 0.9978 

Convergence achieved in 2 iter. (rel. changes 0)

Die segmented()- Funktion erkennt einen Haltepunkt bei x = 8,762.

Das angepasste stückweise Regressionsmodell lautet:

Wenn x ≤ 8,762: y = 0,32143 + 1,59524*(x)

Wenn x > 8,762: y = 0,32143 + 1,59524*(8,762) + (1,59524+2,40476)*(x-8,762)

Angenommen, wir haben einen Wert von x = 5 . Der geschätzte Wert wäre:

• y = 0,32143 + 1,59524*(x)
• y = 0,32143 + 1,59524*(5)
• y = 8,297

Oder nehmen wir an, wir haben einen Wert von x = 12 . Der geschätzte Wert wäre:

• y = 0,32143 + 1,59524*(8,762) + (1,59524+2,40476)*(12-8,762)
• y = 27,25

Schritt 4: Visualisieren Sie das endgültige stückweise Regressionsmodell

Wir können den folgenden Code verwenden, um das endgültige stückweise Regressionsmodell auf unseren Originaldaten zu visualisieren:

 #plot original data
plot(df$x, df$y, pch= 16 , col=' steelblue ')

#add segmented regression model
plot(segmented. fit , add= T )

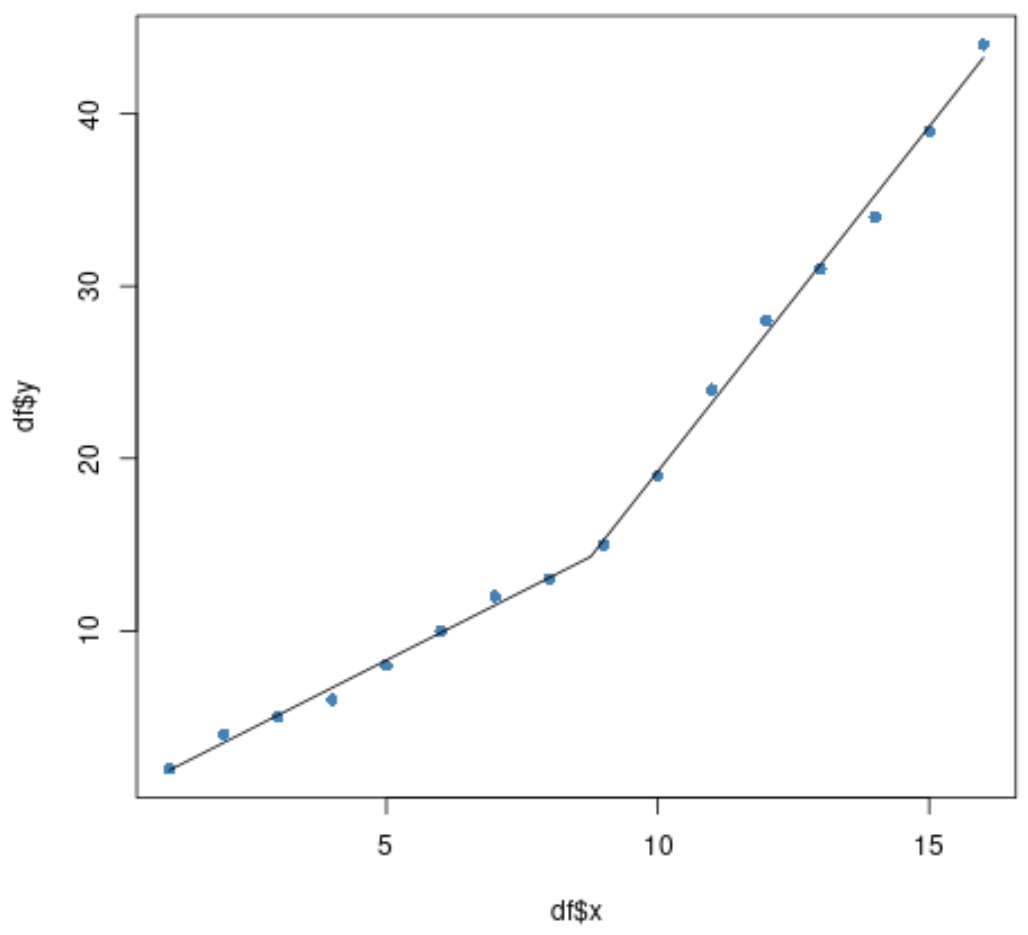
Es scheint, dass das stückweise Regressionsmodell recht gut zu den Daten passt.

Zusätzliche Ressourcen

Die folgenden Tutorials bieten zusätzliche Informationen zu Regressionsmodellen in R:

So führen Sie eine einfache lineare Regression in R durch
So führen Sie eine multiple lineare Regression in R durch
So führen Sie eine logistische Regression in R durch
So führen Sie eine Quantilregression in R durch
So führen Sie eine gewichtete Regression in R durch