So berechnen sie studentisierte residuen in python

Ein Studentenresiduum ist einfach ein Residuum dividiert durch seine geschätzte Standardabweichung.

In der Praxis sagen wir im Allgemeinen, dass jede Beobachtung in einem Datensatz, deren Studentenresiduum größer als ein absoluter Wert von 3 ist, ein Ausreißer ist.

Mit der Funktion OLSResults.outlier_test() von statsmodels, die die folgende Syntax verwendet, können wir schnell die studentisierten Residuen eines Regressionsmodells in Python erhalten:

OLSResults.outlier_test()

Dabei ist OLSResults der Name einer linearen Modellanpassung mit der Funktion statsmodels ols() .

Beispiel: Berechnung studentisierter Residuen in Python

Angenommen, wir erstellen das folgende einfache lineare Regressionsmodell in Python:

 #import necessary packages and functions
import numpy as np
import pandas as pd
import statsmodels. api as sm
from statsmodels. formula . api import ols

#create dataset
df = pd. DataFrame ({'rating': [90, 85, 82, 88, 94, 90, 76, 75, 87, 86],
                   'points': [25, 20, 14, 16, 27, 20, 12, 15, 14, 19]})

#fit simple linear regression model
model = ols('rating ~ points', data=df). fit ()

Wir können die Funktion outlier_test() verwenden, um einen DataFrame zu erstellen, der die studentisierten Residuen für jede Beobachtung im Datensatz enthält:

 #calculate studentized residuals
stud_res = model. outlier_test ()

#display studentized residuals
print(stud_res)

    student_resid unadj_p bonf(p)
0 -0.486471 0.641494 1.000000
1 -0.491937 0.637814 1.000000
2 0.172006 0.868300 1.000000
3 1.287711 0.238781 1.000000
4 0.106923 0.917850 1.000000
5 0.748842 0.478355 1.000000
6 -0.968124 0.365234 1.000000
7 -2.409911 0.046780 0.467801
8 1.688046 0.135258 1.000000
9 -0.014163 0.989095 1.000000

Dieser DataFrame zeigt die folgenden Werte für jede Beobachtung im Datensatz an:

• Der studentisierte Rückstand
• Der nicht angepasste p-Wert des studentisierten Residuums
• Der Bonferroni-korrigierte p-Wert des Studentenresiduals

Wir können sehen, dass das studentisierte Residuum für die erste Beobachtung im Datensatz -0,486471 beträgt, das studentisierte Residuum für die zweite Beobachtung -0,491937 und so weiter.

Wir können auch eine schnelle Darstellung der Werte der Prädiktorvariablen gegenüber den entsprechenden studentisierten Residuen erstellen:

 import matplotlib. pyplot as plt

#define predictor variable values and studentized residuals
x = df[' points ']
y = stud_res[' student_resid ']

#create scatterplot of predictor variable vs. studentized residuals
plt. scatter (x,y)
plt. axhline (y=0, color=' black ', linestyle=' -- ')
plt. xlabel (' Points ')
plt. ylabel (' Studentized Residuals ') 

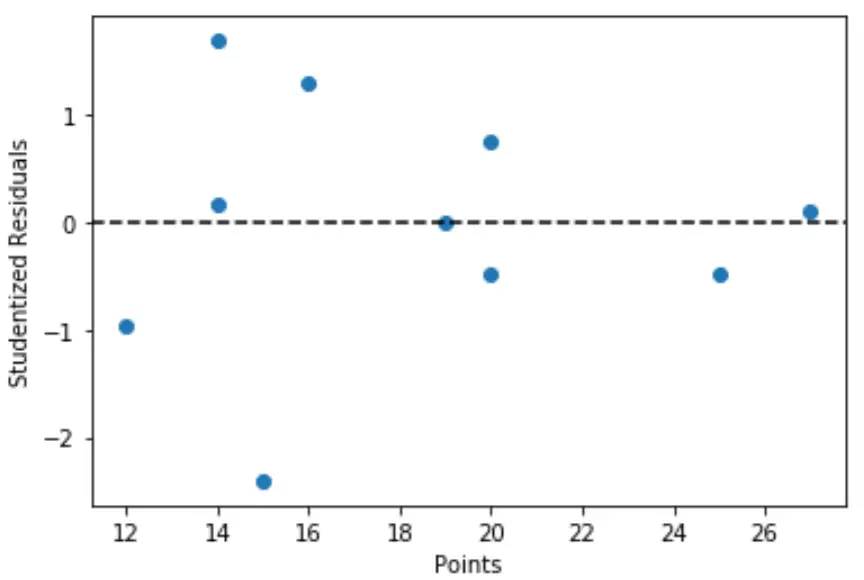
Aus der Grafik können wir ersehen, dass keine der Beobachtungen ein Student-Residuum mit einem absoluten Wert von mehr als 3 aufweist, sodass es im Datensatz keine klaren Ausreißer gibt.

Zusätzliche Ressourcen

So führen Sie eine einfache lineare Regression in Python durch
So führen Sie eine multiple lineare Regression in Python durch
So erstellen Sie ein Restdiagramm in Python