Symmetrische verteilung

In diesem Artikel erfahren Sie, was symmetrische Verteilungen sind, Beispiele für symmetrische Verteilungen und wie Sie bestimmen, ob eine Verteilung symmetrisch oder asymmetrisch ist.

Was ist eine symmetrische Verteilung?

In der Statistik ist eine symmetrische Verteilung eine Verteilung, die links vom Mittelwert die gleiche Anzahl an Werten aufweist wie rechts vom Mittelwert. Mit anderen Worten: Bei einer symmetrischen Verteilung ist der Mittelwert eine Symmetrieachse.

Beispielsweise ist die Normalverteilung eine symmetrische Verteilung.

Bei allen symmetrischen Verteilungen ist der Mittelwert gleich dem Median. Wenn die Verteilung jedoch auch unimodal ist (der statistische Modus ist ein einzelner Wert), sind Mittelwert, Median und Modus gleichwertig.

Um vollständig zu verstehen, was eine symmetrische Verteilung ist, müssen Sie sich logischerweise darüber im Klaren sein, was Mittelwert, Median und Modus sind. Die Bedeutung dieser statistischen Konzepte können Sie hier nachlesen:

Beispiele für symmetrische Verteilungen

Betrachtet man die Definition der symmetrischen Verteilung, so ist unten ein Beispiel für diesen Verteilungstyp dargestellt:

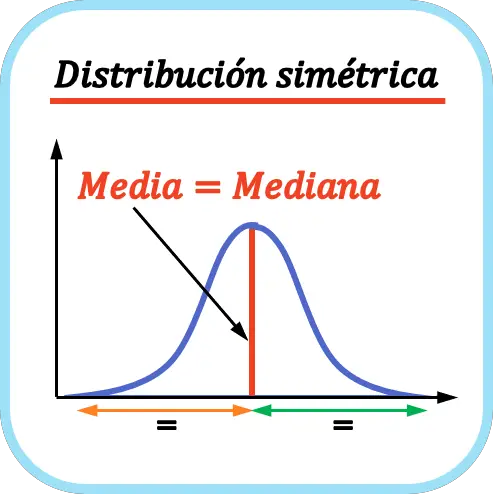
Wie die Grafik zeigt, ist die Verteilung symmetrisch, da der Mittelwert genau in der Mitte aller Daten liegt, d. h. der Rand links der Kurve ist derselbe wie der Rand rechts. In diesem Fall sind Mittelwert, Median und Modus gleich, da der Modus unimodal ist.

Zwei klare Beispiele für zwei verschiedene Arten symmetrischer Wahrscheinlichkeitsverteilungen sind die Normalverteilung und die Gleichverteilung, da sie links und rechts vom Mittelwert die gleiche Anzahl von Werten aufweisen.

Andererseits kann eine Verteilung auch symmetrisch und bimodal sein, also zwei Modi aufweisen. Schauen Sie sich das folgende Beispiel an:

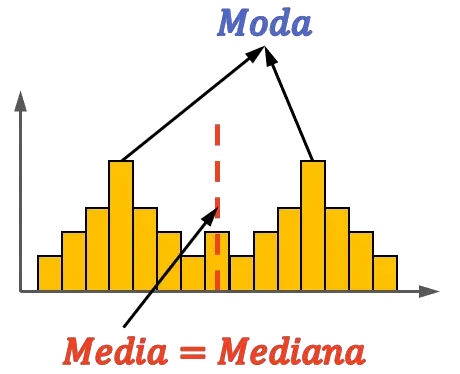
Wie Sie in diesem anderen Beispiel sehen können, kann eine bimodale Verteilung auch symmetrisch sein, da sie unabhängig von anderen Werten den Mittelwert und den Median in der Mitte haben kann. Allerdings muss in diesem Fall der Modus nicht unbedingt gleich dem Mittelwert und dem Modus sein.

Andere Arten von Verteilungen entsprechend ihrer Symmetrie

Neben symmetrischen Verteilungen gibt es zwei weitere Arten asymmetrischer Verteilungen.

• Symmetrische Verteilung : Die Verteilung hat links und rechts vom Mittelwert die gleiche Anzahl von Werten.
• Positiv schiefe Verteilung : Die Verteilung weist rechts vom Mittelwert mehr unterschiedliche Werte auf als links davon.
• Negativ schiefe Verteilung : Die Verteilung hat links vom Mittelwert mehr unterschiedliche Werte als rechts davon.

So erkennen Sie, ob eine Verteilung symmetrisch ist

Um festzustellen, ob eine Verteilung symmetrisch ist oder nicht, müssen wir den Pearson-Asymmetriekoeffizienten berechnen, dessen Formel lautet:

Gold

ist der Pearson-Koeffizient,

das arithmetische Mittel,

der Modus (Statistik) und

die Standardabweichung.

Abhängig vom Vorzeichen des Pearson-Asymmetriekoeffizienten ist die Verteilung also symmetrisch oder asymmetrisch:

• Wenn der Pearson-Skewness-Koeffizient positiv ist, bedeutet dies, dass die Verteilung positiv schief ist.
• Wenn der Pearson-Skewness-Koeffizient negativ ist, bedeutet dies, dass die Verteilung negativ schief ist.
• Wenn der Pearson-Schiefekoeffizient Null ist, bedeutet dies, dass die Verteilung symmetrisch ist.

Der Pearson-Koeffizient kann jedoch nur berechnet werden, wenn die Verteilung unimodal ist, andernfalls muss der Fisher-Asymmetriekoeffizient verwendet werden, dessen Formel wie folgt lautet:

Gold

das arithmetische Mittel,

die Standardabweichung und

die Gesamtzahl der Daten.

Die Interpretation des Fisher-Asymmetriekoeffizienten ist identisch mit der des Pearson-Koeffizienten: Wenn er positiv ist, bedeutet dies, dass die Verteilung positiv asymmetrisch ist, wenn er negativ ist, ist die Verteilung negativ asymmetrisch, und wenn er Null ist, bedeutet dies, dass die Verteilung symmetrisch ist.