So führen sie einen korrelations-t-test durch

Ein Pearson-Korrelationskoeffizient wird verwendet, um den linearen Zusammenhang zwischen zwei Variablen zu quantifizieren.

Es nimmt immer einen Wert zwischen -1 und 1 an, wobei:

• -1 zeigt eine vollkommen negative lineare Korrelation an.
• 0 bedeutet keine lineare Korrelation.
• 1 zeigt eine vollkommen positive lineare Korrelation an.

Um festzustellen, ob ein Korrelationskoeffizient statistisch signifikant ist, können Sie einen T-Test durchführen, bei dem ein T-Score und ein entsprechender p-Wert berechnet werden.

Die Formel zur Berechnung des T-Scores lautet wie folgt:

t = r√ (n-2) / (1-r ² )

Gold:

• r: Der Korrelationskoeffizient
• n: Die Stichprobengröße

Der p-Wert wird als entsprechender zweiseitiger p-Wert für die t-Verteilung mit n-2 Freiheitsgraden berechnet.

Das folgende Beispiel zeigt, wie ein t-Test für einen Korrelationskoeffizienten durchgeführt wird.

Beispiel: Durchführung eines T-Tests zur Korrelation

Angenommen, wir haben den folgenden Datensatz mit zwei Variablen:

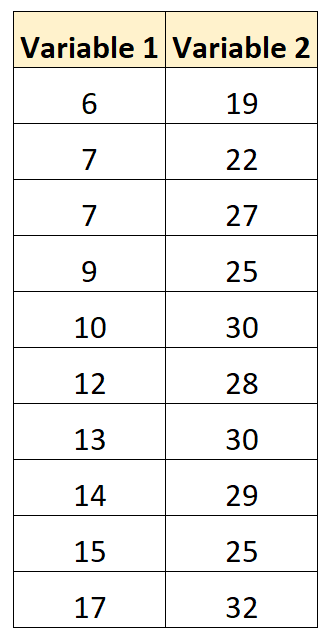
Mit einer Statistiksoftware (Excel, R, Python usw.) können wir den Korrelationskoeffizienten zwischen den beiden Variablen auf 0,707 berechnen.

Dies ist eine sehr positive Korrelation, aber um festzustellen, ob sie statistisch signifikant ist, müssen wir den entsprechenden t-Score und p-Wert berechnen.

Wir können den T-Score wie folgt berechnen:

• t = r√ (n-2) / (1-r ² )
• t = 0,707√ (10-2) / (1-0,707 ² )
• t = 2,828

Mithilfe eines P-Wert-T-Score-Rechners ermitteln wir, dass der entsprechende p-Wert 0,022 beträgt.

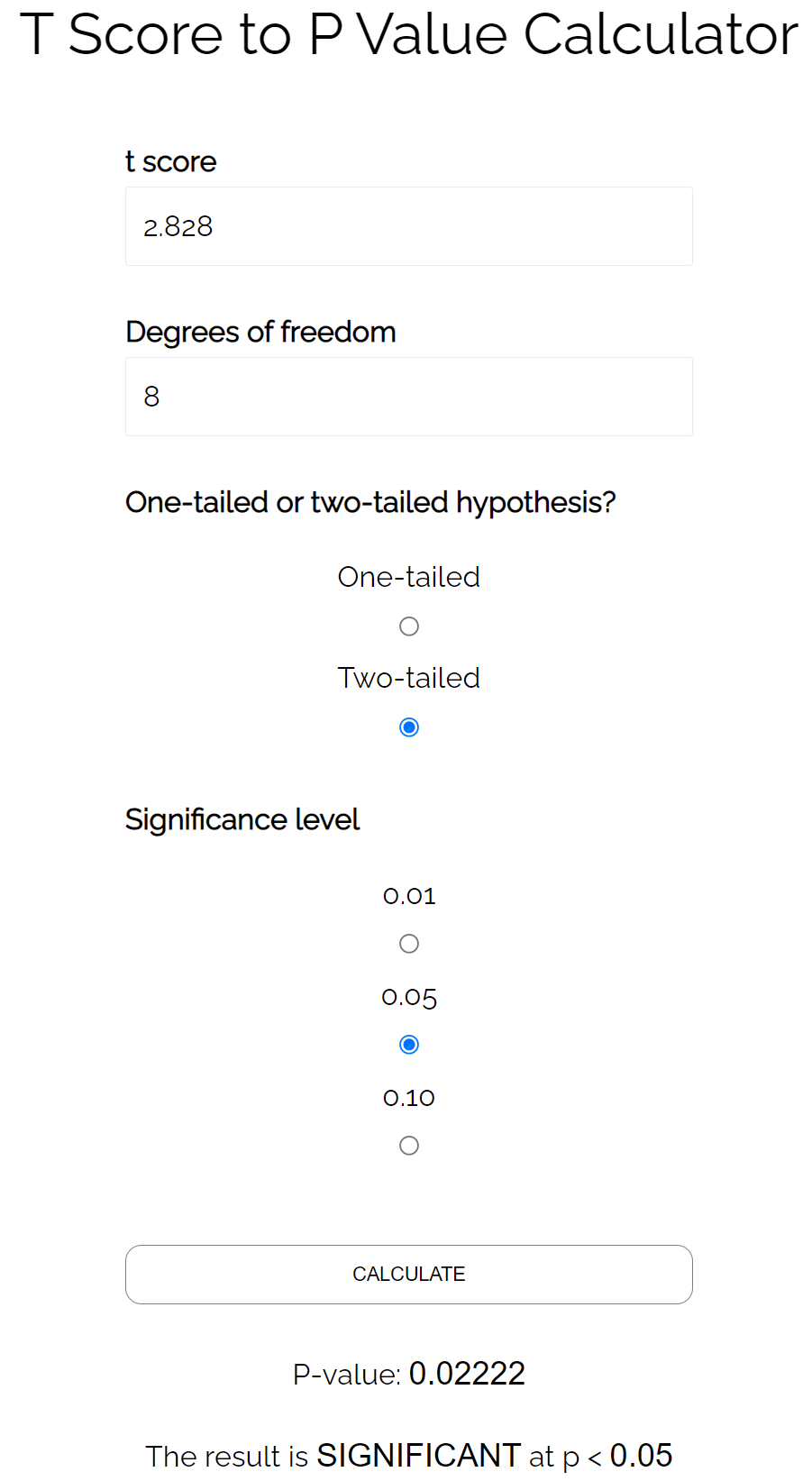
Da dieser p-Wert kleiner als 0,05 ist, würden wir daraus schließen, dass die Korrelation zwischen diesen beiden Variablen statistisch signifikant ist.

Zusätzliche Ressourcen

So führen Sie einen Korrelationstest in Excel durch
So führen Sie einen Korrelationstest in R durch
Was gilt als „schwache“ Korrelation?
Was gilt als „starke“ Korrelation?