So verwenden sie die t-verteilung in python

Die t-Verteilung ist eine Wahrscheinlichkeitsverteilung ähnlich der Normalverteilung , außer dass sie schwerere „Schwänze“ als die Normalverteilung aufweist.

Mit anderen Worten: Im Vergleich zur Normalverteilung befinden sich in der Verteilung mehr Werte an den Enden als in der Mitte:

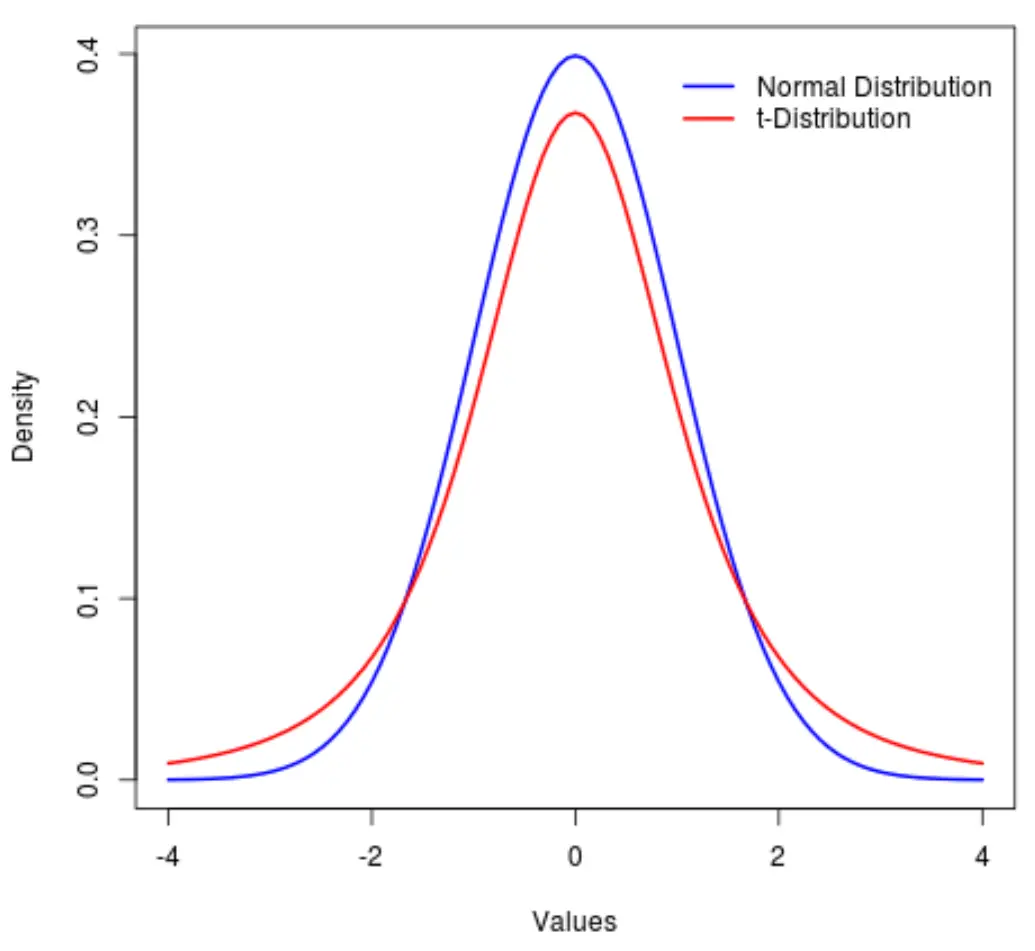
In diesem Tutorial wird erklärt, wie Sie die t-Verteilung in Python verwenden.

Wie man generiert, um es zu verteilen

Mit der Funktion t.rvs(df, size) können Sie Zufallswerte aus einer Verteilung mit bestimmten Freiheitsgraden und Stichprobengrößen generieren:

 from scipy. stats import t

#generate random values from t distribution with df=6 and sample size=10
t. rvs (df= 6 , size= 10 )

array([-3.95799716, -0.01099963, -0.55953846, -1.53420055, -1.41775611,
       -0.45384974, -0.2767931, -0.40177789, -0.3602592, 0.38262431])

Das Ergebnis ist eine Tabelle mit 10 Werten, die gemäß einer Verteilung mit 6 Freiheitsgraden aufeinander folgen.

So berechnen Sie P-Werte mithilfe der t-Verteilung

Wir können die Funktion t.cdf(x, df, loc=0, scale=1) verwenden, um den p-Wert zu finden, der einer t-Test-Statistik zugeordnet ist.

Beispiel 1: Finden eines einseitigen P-Werts

Angenommen, wir führen einen einseitigen Hypothesentest durch und erhalten eine Teststatistik von -1,5 und Freiheitsgrade = 10 .

Wir können die folgende Syntax verwenden, um den p-Wert zu berechnen, der dieser Teststatistik entspricht:

 from scipy. stats import t

#calculate p-value
t. cdf (x=-1.5, df=10)

0.08225366322272008

Der einseitige p-Wert, der der Teststatistik von -1,5 mit 10 Freiheitsgraden entspricht, beträgt 0,0822 .

Beispiel 2: Ermitteln eines Zwei-Wege-P-Werts

Angenommen, wir führen einen zweiseitigen Hypothesentest durch und erhalten eine Teststatistik von 2,14 und Freiheitsgrade = 20 .

Wir können die folgende Syntax verwenden, um den p-Wert zu berechnen, der dieser Teststatistik entspricht:

 from scipy. stats import t

#calculate p-value
(1 - t. cdf (x=2.14, df=20)) * 2

0.04486555082549959

Der zweiseitige p-Wert, der der Teststatistik von 2,14 mit 20 Freiheitsgraden entspricht, beträgt 0,0448 .

Hinweis : Sie können diese Antworten mit dem Rechner für die inverse t-Verteilung überprüfen.

So verfolgen Sie die Verteilung

Sie können die folgende Syntax verwenden, um eine Verteilung mit bestimmten Freiheitsgraden darzustellen:

 from scipy. stats import t
import matplotlib. pyplot as plt

#generate t distribution with sample size 10000
x = t. rvs (df= 12 , size= 10000 )

#create plot of t distribution
plt. hist (x, density= True , edgecolor=' black ', bins= 20 )

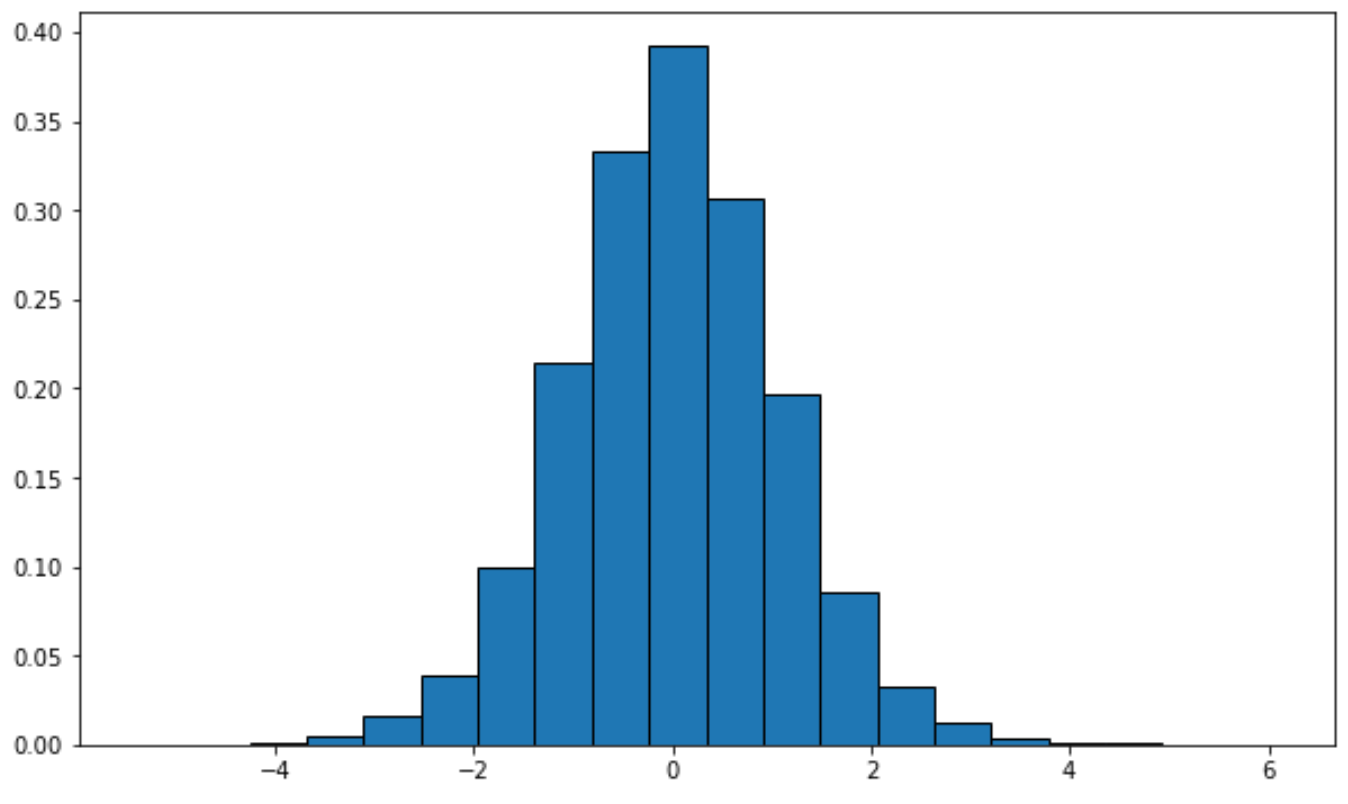
Alternativ können Sie mit dem Seaborn -Visualisierungspaket eine Dichtekurve erstellen:

 import seaborn as sns

#create density curve
sns. kdeplot (x)

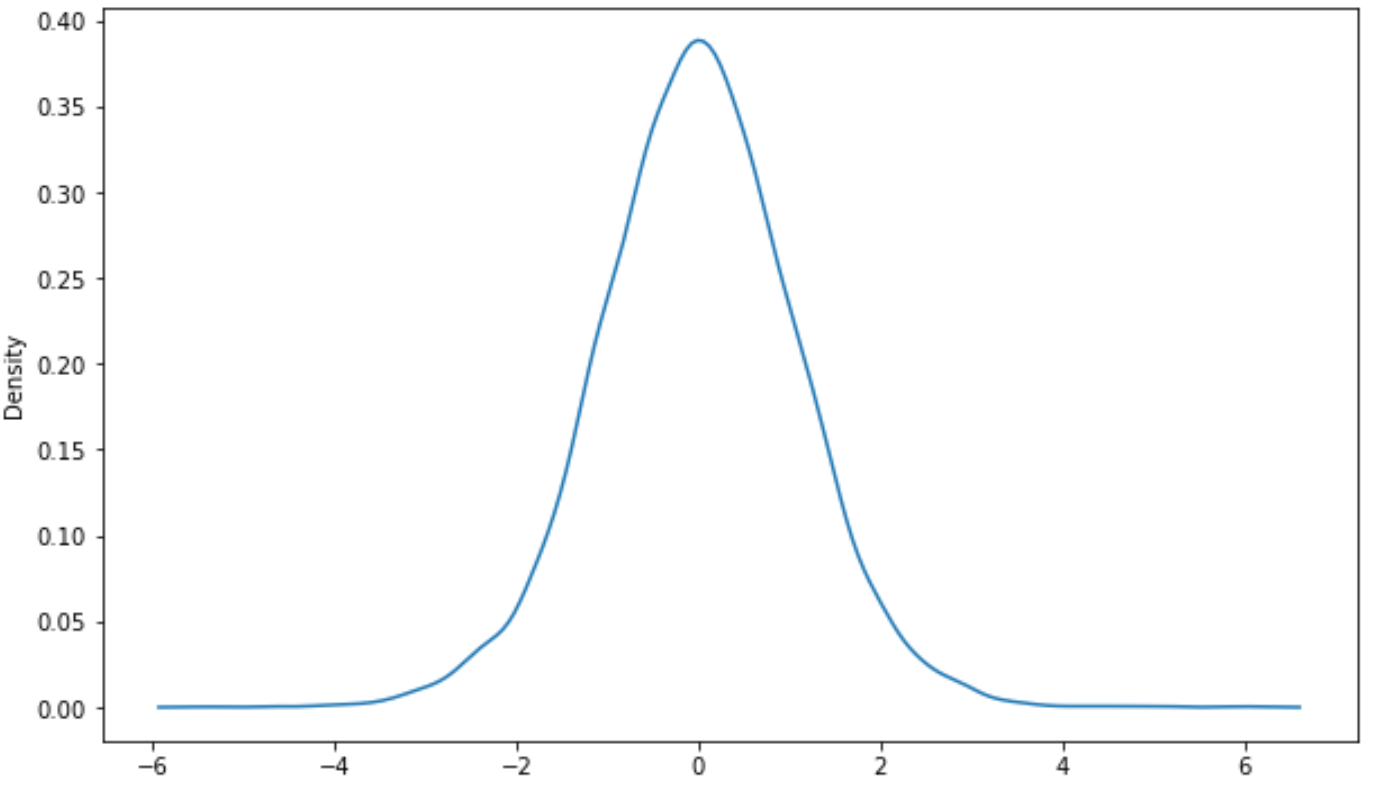
Zusätzliche Ressourcen

Die folgenden Tutorials bieten zusätzliche Informationen zur Verteilung:

Normalverteilung vs. t-Verteilung: Was ist der Unterschied?
Inverser T-Verteilungsrechner