T-score vs. z-score: wann werden sie verwendet?
Zwei Begriffe, die Studierende in Statistikkursen oft verwirren, sind T-Scores und Z-Scores .
Beide werden häufig zum Testen von Hypothesen oder zum Erstellen von Konfidenzintervallen verwendet, unterscheiden sich jedoch geringfügig.
Hier ist die Formel für jeden:
Punktzahl t = ( x – μ) / (s/√ n )
Gold:
- x : Stichprobenmittel
- μ : Bevölkerungsdurchschnitt
- s : Standardabweichung der Stichprobe
- n : Stichprobengröße
z-Score = ( x – μ) / σ
Gold:
- x : Rohdatenwert
- μ : Bevölkerungsdurchschnitt
- σ : Populationsstandardabweichung
Dieses Flussdiagramm zeigt, wann Sie die einzelnen Elemente basierend auf Ihren Daten verwenden sollten:
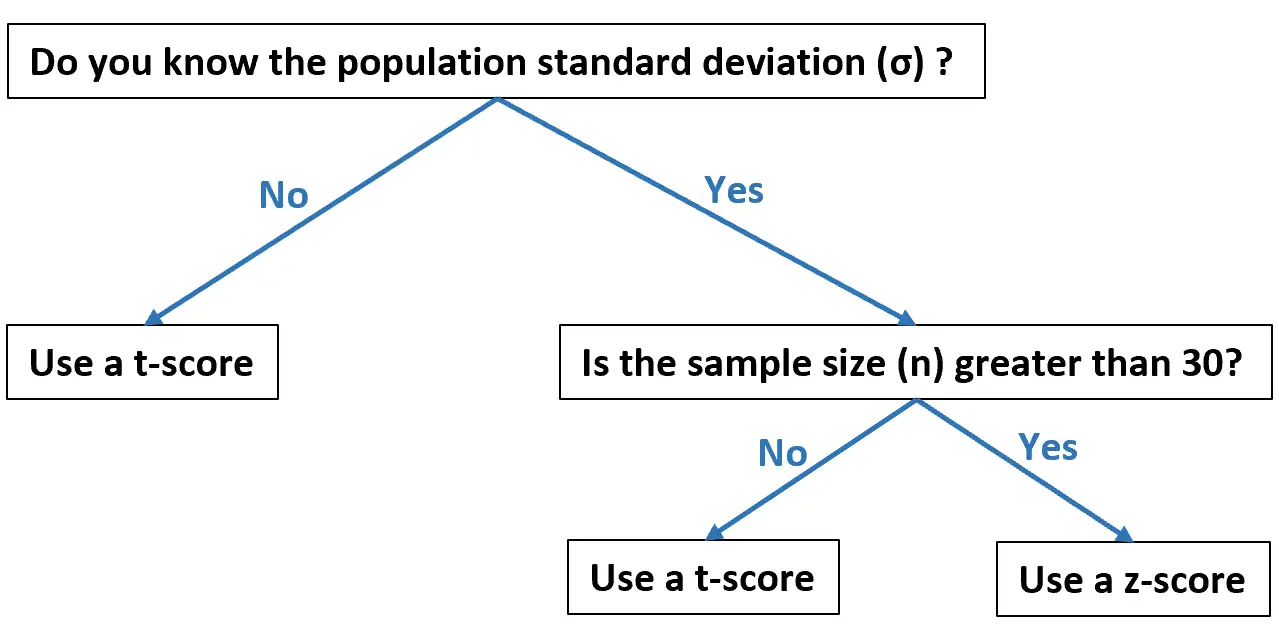
Die folgenden Beispiele zeigen, wie man in der Praxis einen T-Score und einen Z-Score berechnet.
Beispiel 1: Berechnung eines T-Scores
Angenommen, ein Restaurant bereitet Hamburger zu, die angeblich ein Durchschnittsgewicht von μ = 0,25 Pfund haben.
Angenommen, wir nehmen eine Zufallsstichprobe von n = 20 Hamburgern und stellen fest, dass das mittlere Gewicht der Stichprobe x = 0,22 Pfund mit einer Standardabweichung von s = 0,05 Pfund beträgt. Führen Sie einen Hypothesentest durch, um festzustellen, ob das tatsächliche Durchschnittsgewicht aller von diesem Restaurant produzierten Hamburger 0,25 Pfund beträgt.
In diesem Beispiel würden wir einen T-Score zur Durchführung des Hypothesentests verwenden, da keine der folgenden beiden Bedingungen erfüllt ist.
- Die Populationsstandardabweichung (σ) ist bekannt. (σ wird in diesem Beispiel nicht angegeben)
- Die Stichprobengröße ist größer als 30. (n=20 in diesem Beispiel)
Wir würden den T-Score also wie folgt berechnen:
- Punktzahl t = ( x – μ) / (s/√ n )
- t-Score = (0,22 – 0,25) / (0,05 / √ 20 )
- t-Score = -2,68
Laut dem P-Wert-T-Score-Rechner beträgt der p-Wert, der diesem T-Score entspricht, 0,01481 .
Da dieser p-Wert unter 0,05 liegt, haben wir genügend Beweise dafür, dass das durchschnittliche Gewicht der in diesem Restaurant hergestellten Hamburger nicht 0,25 Pfund beträgt.
Beispiel 2: Berechnung eines Z-Scores
Angenommen, ein Unternehmen stellt Batterien her, deren Lebensdauer bekanntermaßen einer Normalverteilung mit einem Mittelwert von μ = 20 Stunden und einer Standardabweichung von σ = 5 Stunden folgt.
Angenommen, wir nehmen eine Zufallsstichprobe von n = 50 Batterien und stellen fest, dass der Stichprobenmittelwert x = 21 Stunden beträgt. Führen Sie einen Hypothesentest durch, um festzustellen, ob die tatsächliche durchschnittliche Lebensdauer aller von diesem Unternehmen hergestellten Batterien 20 Stunden beträgt.
In diesem Beispiel würden wir einen Z-Score zur Durchführung des Hypothesentests verwenden, da beide der folgenden Bedingungen erfüllt sind:
- Die Populationsstandardabweichung (σ) ist bekannt. (σ ist in diesem Beispiel gleich 5)
- Die Stichprobengröße ist größer als 30. (n=50 in diesem Beispiel)
Wir würden den Z-Score also wie folgt berechnen:
- z-Score = ( x – μ) / σ
- Z-Score = (21 – 20) / 5
- Z-Score = 0,2
Laut dem P-Wert-Z-Score-Rechner beträgt der p-Wert, der diesem Z-Score entspricht, 0,84184 .
Da dieser p-Wert nicht weniger als 0,05 beträgt, liegen uns keine ausreichenden Beweise dafür vor, dass die durchschnittliche Lebensdauer aller von diesem Unternehmen hergestellten Batterien von 20 Stunden abweicht.
Zusätzliche Ressourcen
Die folgenden Tutorials bieten weitere Informationen zu T-Scores und Z-Scores:
Normalverteilung vs. t-Verteilung: Was ist der Unterschied?
So lesen Sie die Verteilungstabelle t
So lesen Sie die Z-Tabelle