Den t-test in der linearen regression verstehen

Die lineare Regression wird verwendet, um die Beziehung zwischen einer Prädiktorvariablen und einer Antwortvariablen zu quantifizieren.

Wann immer wir eine lineare Regression durchführen, möchten wir wissen, ob eine statistisch signifikante Beziehung zwischen der Prädiktorvariablen und der Antwortvariablen besteht.

Wir testen die Signifikanz, indem wir einen t-Test für die Regressionssteigung durchführen. Für diesen t-Test verwenden wir die folgende Null- und Alternativhypothese:

• H ₀ : β ₁ = 0 (die Steigung ist gleich Null)
• H _A : β ₁ ≠ 0 (die Steigung ist ungleich Null)

Anschließend berechnen wir die Teststatistik wie folgt:

t = b / SE _b

Gold:

• b : Schätzung des Koeffizienten
• SE _b : Standardfehler der Koeffizientenschätzung

Wenn der p-Wert, der t entspricht, unter einem bestimmten Schwellenwert liegt (z. B. α = 0,05), lehnen wir die Nullhypothese ab und kommen zu dem Schluss, dass eine statistisch signifikante Beziehung zwischen der Prädiktorvariablen und der Antwortvariablen besteht.

Das folgende Beispiel zeigt, wie man in der Praxis einen t-Test für ein lineares Regressionsmodell durchführt.

Beispiel: Ausführen eines T-Tests für die lineare Regression

Angenommen, ein Professor möchte für 40 seiner Studenten den Zusammenhang zwischen Lernstunden und Prüfungsnoten analysieren.

Es führt eine einfache lineare Regression durch, wobei die untersuchten Stunden als Prädiktorvariable und die erhaltenen Prüfungsergebnisse als Antwortvariable verwendet werden.

Die folgende Tabelle zeigt die Ergebnisse des Regressionsmodells:

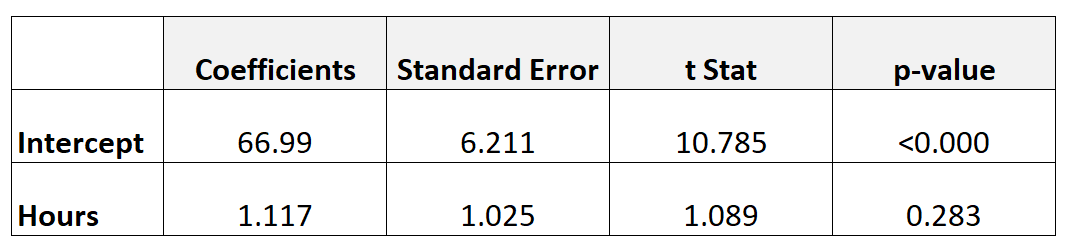
Um festzustellen, ob die gelernten Stunden einen statistisch signifikanten Zusammenhang mit der Abschlussprüfungsnote haben, können wir einen T-Test durchführen.

Für diesen t-Test verwenden wir die folgende Null- und Alternativhypothese:

• H ₀ : β ₁ = 0 (die Steigung der untersuchten Stunden ist gleich Null)
• H _A : β ₁ ≠ 0 (die Steigung der untersuchten Stunden ist ungleich Null)

Anschließend berechnen wir die Teststatistik wie folgt:

• t = b / SE _b
• t = 1,117 / 1,025
• t = 1,089

Der p-Wert, der t = 1,089 mit df = n-2 = 40 – 2 = 38 entspricht, beträgt 0,283 .

Beachten Sie, dass wir diesen p-Wert auch mit dem T-Score-zu-P-Wert-Rechner berechnen können:

Da dieser p-Wert nicht kleiner als 0,05 ist, können wir die Nullhypothese nicht ablehnen.

Dies bedeutet, dass die gelernten Stunden keinen statistisch signifikanten Zusammenhang mit den Abschlussprüfungsergebnissen haben .

Zusätzliche Ressourcen

Die folgenden Tutorials bieten zusätzliche Informationen zur linearen Regression:

Einführung in die einfache lineare Regression
Einführung in die multiple lineare Regression
So interpretieren Sie Regressionskoeffizienten
So interpretieren Sie den F-Test für die Gesamtsignifikanz bei der Regression