So führen sie einen t-test mit ungleichen stichprobengrößen durch

Eine häufig gestellte Frage von Studierenden zum Thema Statistik lautet:

Ist es möglich, einen T-Test durchzuführen, wenn die Stichprobengrößen jeder Gruppe nicht gleich sind?

Die kurze Antwort:

Ja, Sie können einen T-Test durchführen, wenn die Stichprobengrößen nicht gleich sind. Gleiche Stichprobengrößen gehören nicht zu den Annahmen eines t-Tests.

Die wirklichen Probleme entstehen, wenn die beiden Stichproben nicht die gleichen Varianzen aufweisen, was eine der Annahmen eines t-Tests ist .

In diesem Fall wird empfohlen, stattdessen den Welch-T-Test zu verwenden, der nicht von gleichen Varianzen ausgeht.

Die folgenden Beispiele zeigen, wie T-Tests mit ungleichen Stichprobengrößen durchgeführt werden, wenn die Varianzen gleich sind und wenn nicht.

Beispiel 1: Ungleiche Stichprobengrößen und gleiche Varianzen

Angenommen, wir verwalten zwei Programme, die Schülern dabei helfen sollen, bei bestimmten Prüfungen bessere Leistungen zu erbringen.

Die Ergebnisse sind wie folgt:

Programm 1:

• n (Stichprobengröße): 500
• x (Stichprobendurchschnitt): 80
• s (Standardabweichung der Stichprobe): 5

Programm 2:

• n (Stichprobengröße): 20
• x (Stichprobendurchschnitt): 85
• s (Standardabweichung der Stichprobe): 5

Der folgende Code zeigt, wie man in R einen Boxplot erstellt, um die Verteilung der Prüfungsergebnisse für jedes Programm zu visualisieren:

 #make this example reproducible
set. seeds (1)

#create vectors to hold exam scores
program1 <- rnorm(500, mean=80, sd=5)
program2 <- rnorm(20, mean=85, sd=5)

#create boxplots to visualize distribution of exam scores
boxplot(program1, program2, names=c(" Program 1 "," Program 2 "))

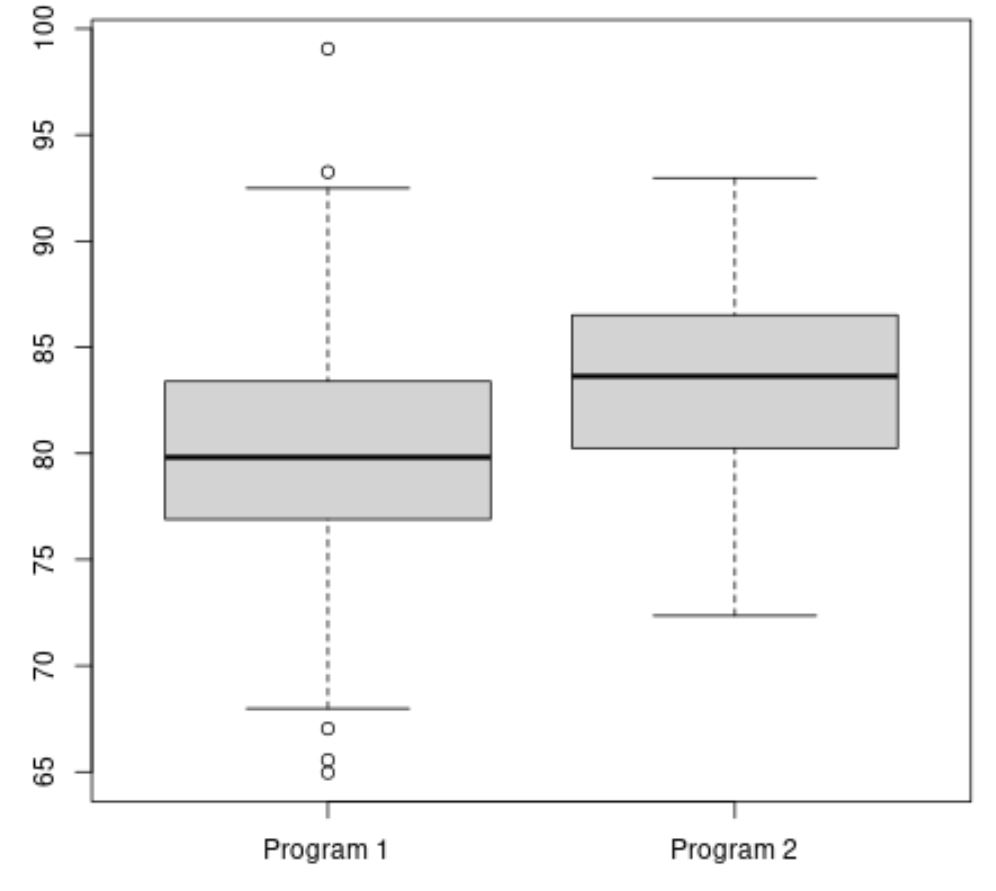
Die durchschnittliche Prüfungspunktzahl für Programm 2 scheint höher zu sein, aber die Abweichung der Prüfungsergebnisse zwischen den beiden Programmen ist ungefähr gleich.

Der folgende Code zeigt, wie ein T-Test für unabhängige Stichproben mit einem Welch-T-Test durchgeführt wird:

 #perform independent samples t-test
t. test (program1, program2, var. equal = TRUE )

	Two Sample t-test

data: program1 and program2
t = -3.3348, df = 518, p-value = 0.0009148
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -6.111504 -1.580245
sample estimates:
mean of x mean of y 
 80.11322 83.95910

#perform Welch's two sample t-test
t. test (program1, program2, var. equal = FALSE )

	Welch Two Sample t-test

data: program1 and program2
t = -3.3735, df = 20.589, p-value = 0.00293
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -6.219551 -1.472199
sample estimates:
mean of x mean of y 
 80.11322 83.95910 

Der T-Test für unabhängige Stichproben gibt einen p-Wert von 0,0009 zurück und der Welch-T-Test gibt einen p-Wert von 0,0029 zurück.

Da der p-Wert jedes Tests kleiner als 0,05 ist, würden wir die Nullhypothese in jedem Test ablehnen und daraus schließen, dass es einen statistisch signifikanten Unterschied in den durchschnittlichen Prüfungsergebnissen zwischen den beiden Programmen gibt.

Auch wenn die Stichprobengrößen ungleich sind, liefern der T-Test unabhängiger Stichproben und der Welch-T-Test ähnliche Ergebnisse, da die beiden Stichproben gleiche Varianzen aufwiesen.

Beispiel 2: Ungleiche Stichprobengrößen und ungleiche Varianzen

Angenommen, wir verwalten zwei Programme, die Schülern dabei helfen sollen, bei bestimmten Prüfungen bessere Leistungen zu erbringen.

Die Ergebnisse sind wie folgt:

Programm 1:

• n (Stichprobengröße): 500
• x (Stichprobendurchschnitt): 80
• s (Standardabweichung der Stichprobe): 25

Programm 2:

• n (Stichprobengröße): 20
• x (Stichprobendurchschnitt): 85
• s (Standardabweichung der Stichprobe): 5

Der folgende Code zeigt, wie man in R einen Boxplot erstellt, um die Verteilung der Prüfungsergebnisse für jedes Programm zu visualisieren:

 #make this example reproducible
set. seeds (1)

#create vectors to hold exam scores
program1 <- rnorm(500, mean=80, sd=25)
program2 <- rnorm(20, mean=85, sd=5)

#create boxplots to visualize distribution of exam scores
boxplot(program1, program2, names=c(" Program 1 "," Program 2 "))

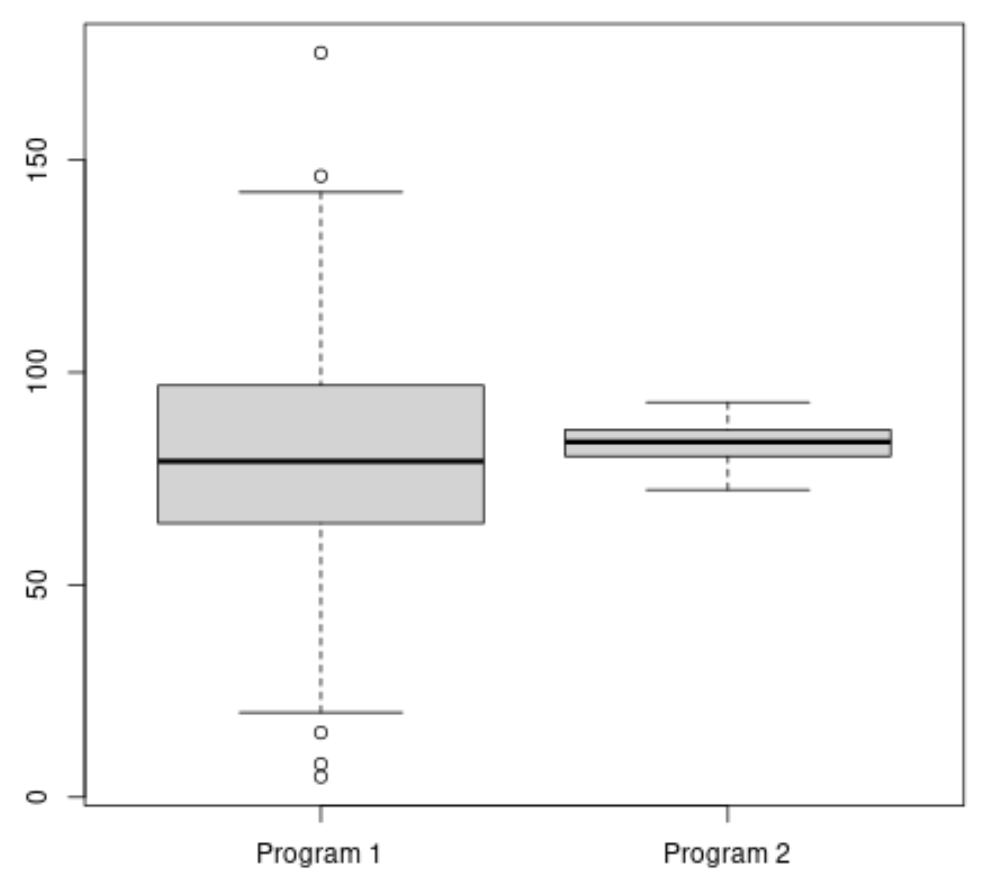
Die durchschnittliche Prüfungspunktzahl für Programm 2 scheint höher zu sein, aber die Varianz der Prüfungsergebnisse für Programm 1 ist viel größer als die für Programm 2.

Der folgende Code zeigt, wie ein T-Test für unabhängige Stichproben mit einem Welch-T-Test durchgeführt wird:

 #perform independent samples t-test
t. test (program1, program2, var. equal = TRUE )

	Two Sample t-test

data: program1 and program2
t = -0.5988, df = 518, p-value = 0.5496
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -14.52474 7.73875
sample estimates:
mean of x mean of y 
  80.5661 83.9591

#perform Welch's two sample t-test
t. test (program1, program2, var. equal = FALSE )

	Welch Two Sample t-test

data: program1 and program2
t = -2.1338, df = 74.934, p-value = 0.03613
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -6.560690 -0.225296
sample estimates:
mean of x mean of y 
  80.5661 83.9591 

Der T-Test für unabhängige Stichproben gibt einen p-Wert von 0,5496 zurück und der Welch-T-Test gibt einen p-Wert von 0,0361 zurück.

Der T-Test bei unabhängigen Stichproben ist nicht in der Lage, einen Unterschied in den durchschnittlichen Prüfungsergebnissen zu erkennen, aber der Welch-T-Test ist in der Lage, einen statistisch signifikanten Unterschied zu erkennen.

Da die beiden Stichproben ungleiche Varianzen aufwiesen, konnte nur der Welch-T-Test den statistisch signifikanten Unterschied in den durchschnittlichen Prüfungsergebnissen erkennen, da dieser Test nicht von gleichen Varianzen zwischen den Stichproben ausgeht .

Zusätzliche Ressourcen

Die folgenden Tutorials bieten zusätzliche Informationen zu T-Tests:

Einführung in den T-Test bei einer Stichprobe
Einführung in den T-Test bei zwei Stichproben
Einführung in den T-Test für gepaarte Stichproben