So führen sie einen teil-f-test in excel durch
Mithilfe eines partiellen F-Tests wird ermittelt, ob ein statistisch signifikanter Unterschied zwischen einem Regressionsmodell und einer verschachtelten Version desselben Modells besteht.
Ein verschachteltes Modell ist einfach ein Modell, das eine Teilmenge von Prädiktorvariablen im gesamten Regressionsmodell enthält.
Angenommen, wir haben das folgende Regressionsmodell mit vier Prädiktorvariablen:
Y = β 0 + β 1 x 1 + β 2 x 2 + β 3 x 3 + β 4 x 4 + ε
Ein Beispiel für ein verschachteltes Modell wäre das folgende Modell mit nur zwei der ursprünglichen Prädiktorvariablen:
Y = β 0 + β 1 x 1 + β 2 x 2 + ε
Um festzustellen, ob sich diese beiden Modelle erheblich unterscheiden, können wir einen partiellen F-Test durchführen, der die folgende F-Test-Statistik berechnet:
F = (( Reduzierter RSS – Vollständiger RSS)/p) / ( Vollständiger RSS /nk)
Gold:
- Reduzierter RSS : Die verbleibende Quadratsumme des reduzierten (dh „verschachtelten“) Modells.
- RSS full : Die verbleibende Quadratsumme des vollständigen Modells.
- p: Anzahl der aus dem vollständigen Modell entfernten Prädiktoren.
- n: die Gesamtzahl der Beobachtungen im Datensatz.
- k: Die Anzahl der Koeffizienten (einschließlich des Achsenabschnitts) im vollständigen Modell.
Dieser Test verwendet die folgenden Null- und Alternativhypothesen :
H 0 : Alle aus dem vollständigen Modell entfernten Koeffizienten sind Null.
H A : Mindestens einer der aus dem vollständigen Modell entfernten Koeffizienten ist ungleich Null.
Wenn der der F-Test-Statistik entsprechende p-Wert unter einem bestimmten Signifikanzniveau (z. B. 0,05) liegt, können wir die Nullhypothese ablehnen und daraus schließen, dass mindestens einer der aus dem vollständigen Modell entfernten Koeffizienten signifikant ist.
Das folgende Beispiel zeigt, wie Sie einen Teil-F-Test in Excel durchführen.
Beispiel: Teil-F-Test in Excel
Angenommen, wir haben den folgenden Datensatz in Excel:
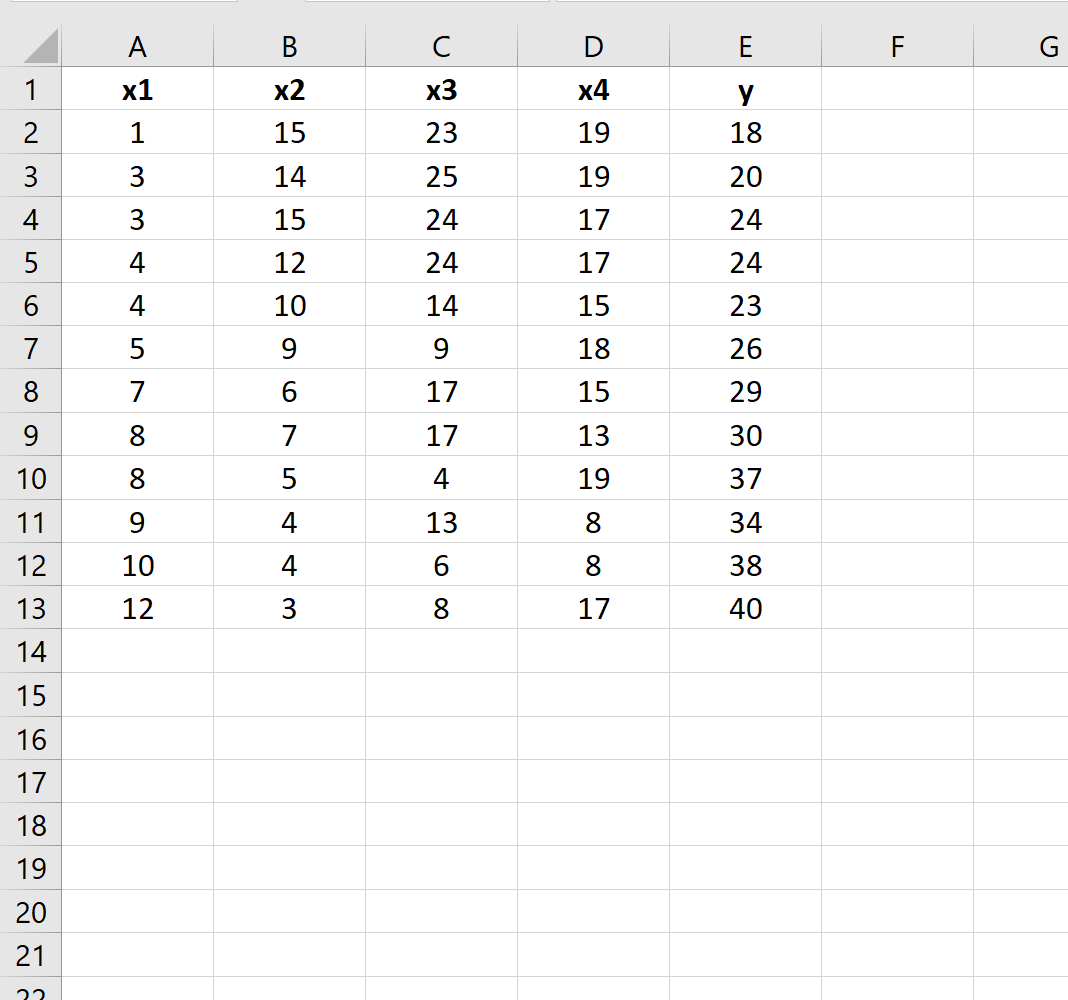
Angenommen, wir möchten feststellen, ob es einen Unterschied zwischen den folgenden beiden Regressionsmodellen gibt:
Vollständiges Modell: y = β 0 + β 1 x 1 + β 2 x 2 + β 3 x 3 + β 4 x 4
Reduziertes Modell: y = β 0 + β 1 x 1 + β 2 x 2
Wir können für jedes Modell eine multiple lineare Regression in Excel durchführen, um das folgende Ergebnis zu erhalten:
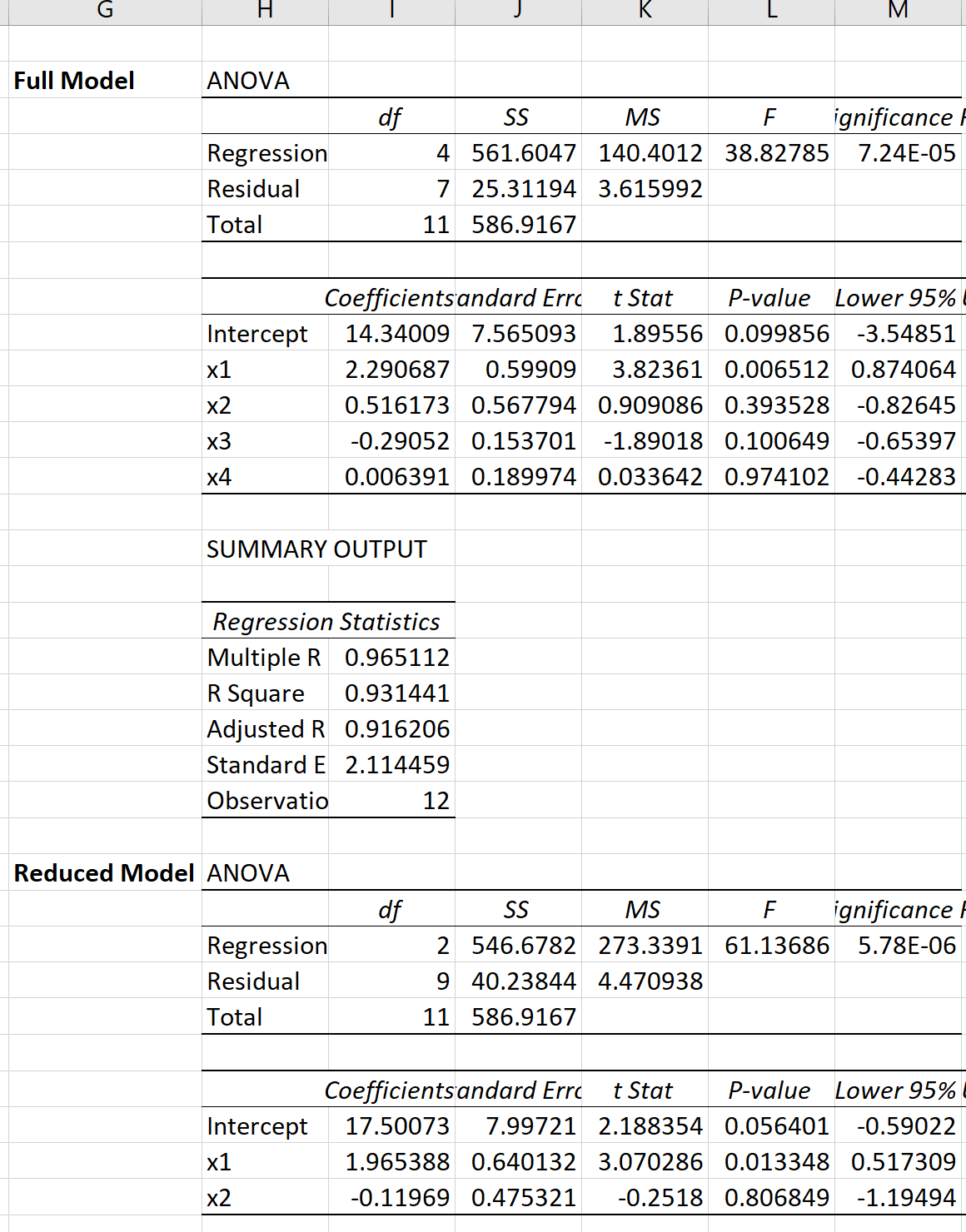
Wir können dann die folgende Formel verwenden, um die F-Test-Statistik für den partiellen F-Test zu berechnen:
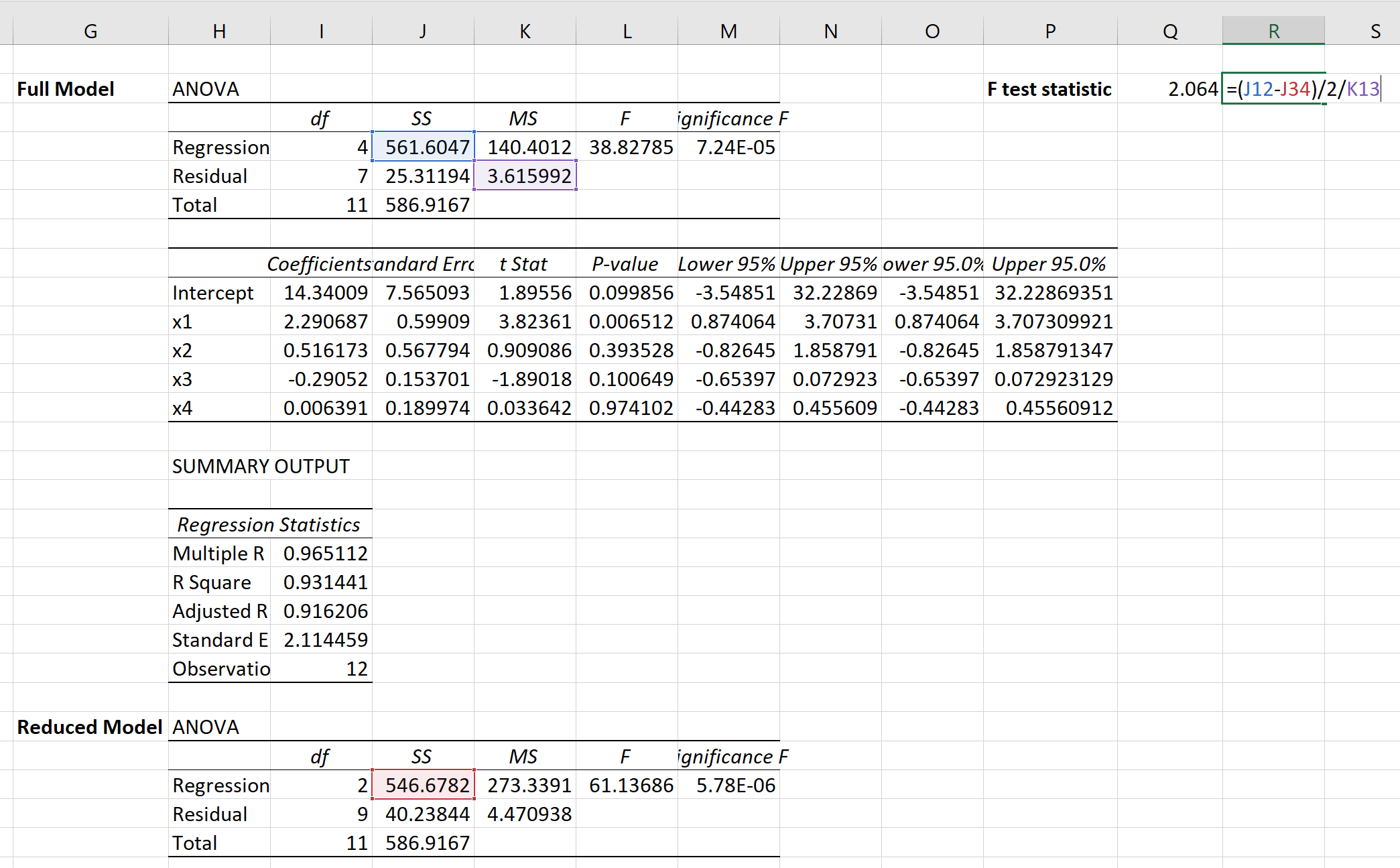
Die Teststatistik beträgt 2,064 .
Mit der folgenden Formel können wir dann den entsprechenden p-Wert berechnen:
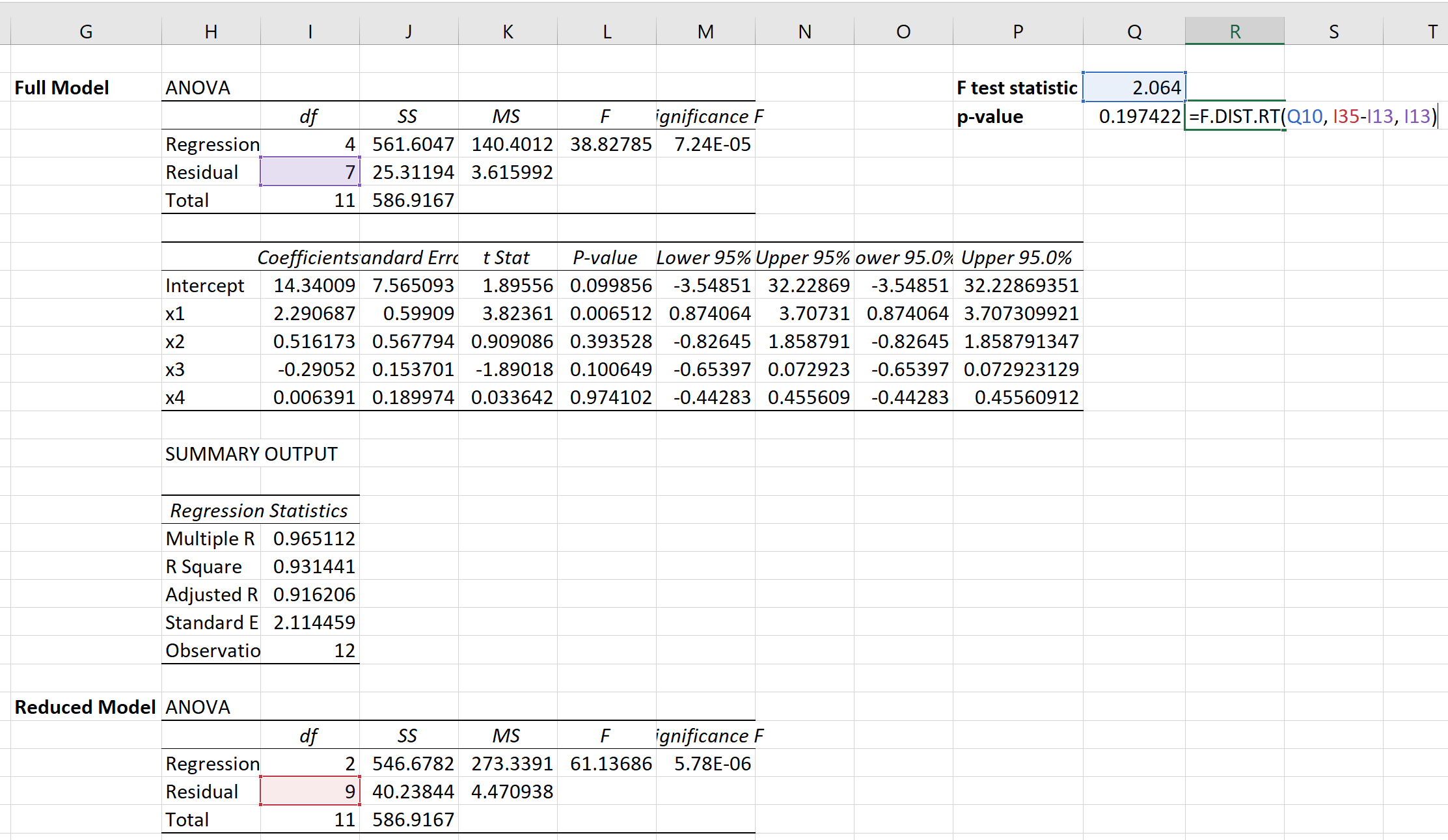
Der p-Wert beträgt 0,1974 .
Da dieser p-Wert nicht kleiner als 0,05 ist, können wir die Nullhypothese nicht ablehnen. Das bedeutet, dass wir nicht über genügend Beweise verfügen, um zu sagen, dass eine der x3- oder x4- Prädiktorvariablen statistisch signifikant ist.
Mit anderen Worten: Das Hinzufügen von x3 und x4 zum Regressionsmodell verbessert die Modellanpassung nicht wesentlich.
Zusätzliche Ressourcen
So führen Sie eine einfache lineare Regression in Excel durch
So führen Sie eine multiple lineare Regression in Excel durch
So berechnen Sie den Standardfehler der Regression in Excel
Über den Autor
Dr. Benjamin Anderson
Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen