So führen sie eine quadratische regression auf einem ti-84-rechner durch

Wenn zwei Variablen eine lineare Beziehung haben, können wir oft eine einfache lineare Regression verwenden , um ihre Beziehung zu quantifizieren.

Wenn jedoch zwei Variablen in einer quadratischen Beziehung stehen, können wir die quadratische Regression verwenden, um ihre Beziehung zu quantifizieren.

In diesem Tutorial wird erläutert, wie Sie eine quadratische Regression auf einem TI-84-Rechner durchführen.

Beispiel: Quadratische Regression auf einem TI-84-Rechner

Angenommen, wir möchten den Zusammenhang zwischen der Anzahl der geleisteten Arbeitsstunden und dem Glück verstehen. Wir haben die folgenden Daten zur Anzahl der pro Woche geleisteten Arbeitsstunden und zum gemeldeten Grad der Zufriedenheit (auf einer Skala von 0 bis 100) für 11 verschiedene Personen:

Befolgen Sie die folgenden Schritte, um eine quadratische Regression auf einem TI-84-Rechner durchzuführen.

Schritt 1: Visualisieren Sie die Daten.

Bevor wir die quadratische Regression verwenden können, müssen wir sicherstellen, dass die Beziehung zwischen der erklärenden Variablen (Stunden) und der Antwortvariablen (Glück) tatsächlich quadratisch ist.

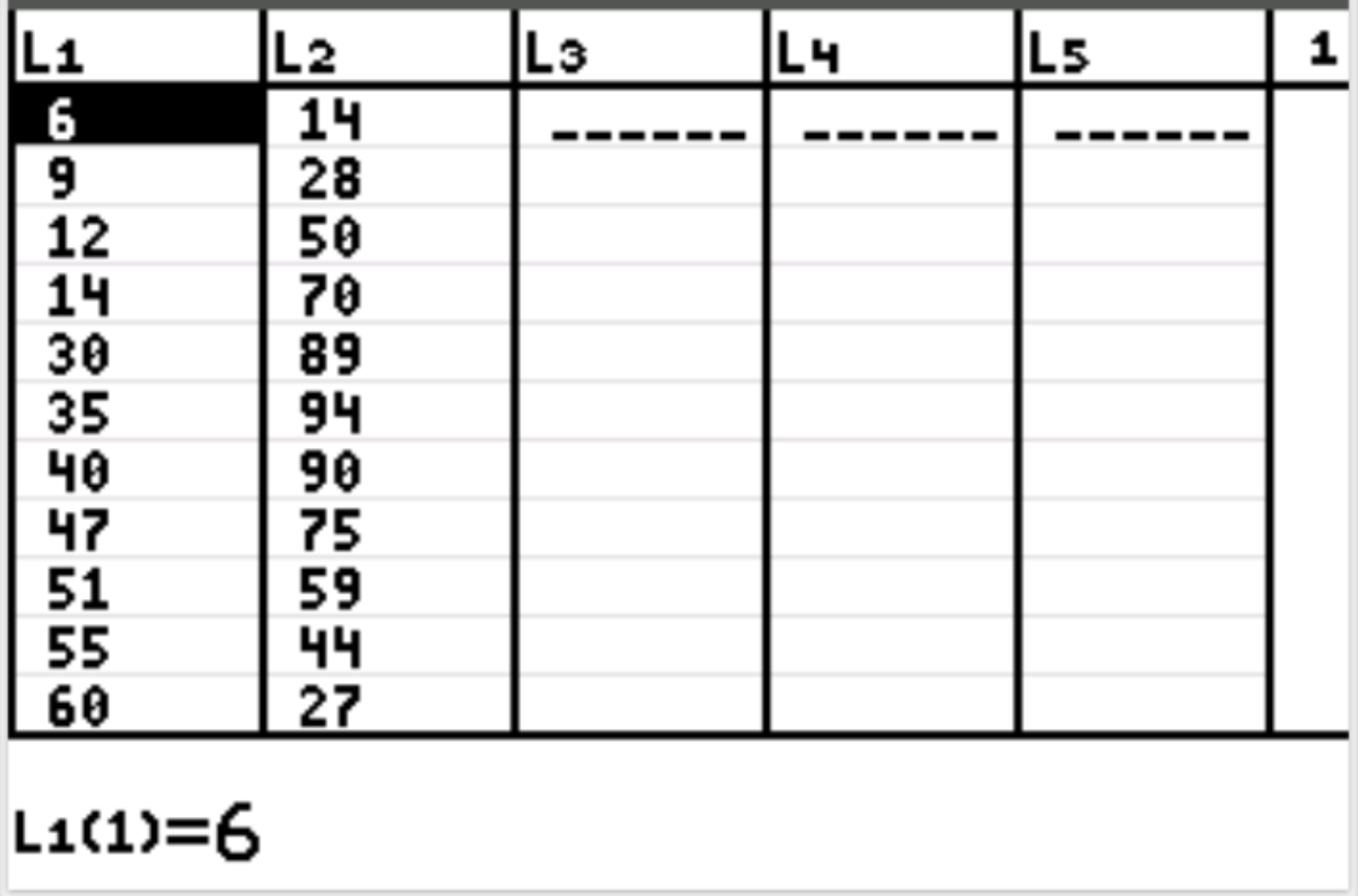
Zuerst geben wir die Datenwerte für die erklärende Variable und die Antwortvariable ein. Drücken Sie Stat und dann EDIT . Tragen Sie in Spalte L1 folgende Werte für die erklärende Variable (geleistete Arbeitsstunden) und in Spalte L2 die Werte für die Antwortvariable (Glück) ein:

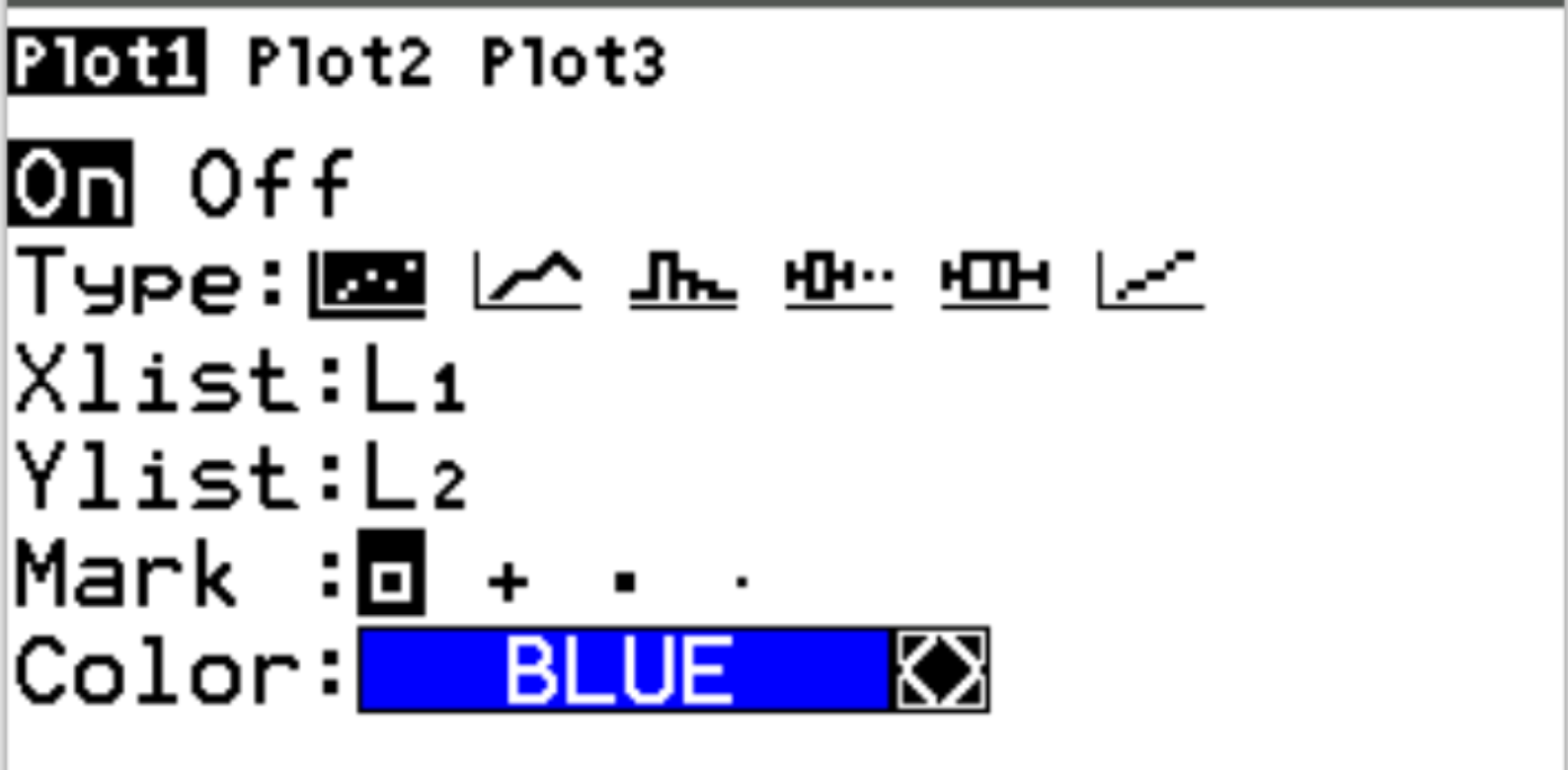
Drücken Sie als Nächstes die 2. Taste und dann y=, um auf das Statplot- Menü zuzugreifen. Markieren Sie Plot1 und drücken Sie die Eingabetaste . Stellen Sie sicher, dass das Plotten aktiviert ist und L1 und L2 für Xlist bzw. Ylist ausgewählt sind:

Drücken Sie anschließend Zoom und dann 9:ZoomStat . Dadurch wird automatisch die folgende Punktwolke erstellt:

Wir können sehen, dass das Glück tendenziell zunimmt, wenn die Anzahl der geleisteten Arbeitsstunden von Null auf einen bestimmten Punkt ansteigt, dann aber zu sinken beginnt, wenn die Anzahl der geleisteten Arbeitsstunden weiter zunimmt.

Diese umgekehrte „U“-Form im Streudiagramm weist darauf hin, dass zwischen geleisteten Arbeitsstunden und Glück ein quadratischer Zusammenhang besteht, was bedeutet, dass wir zur Quantifizierung dieses Zusammenhangs eine quadratische Regression verwenden sollten.

Schritt 2: Führen Sie eine quadratische Regression durch.

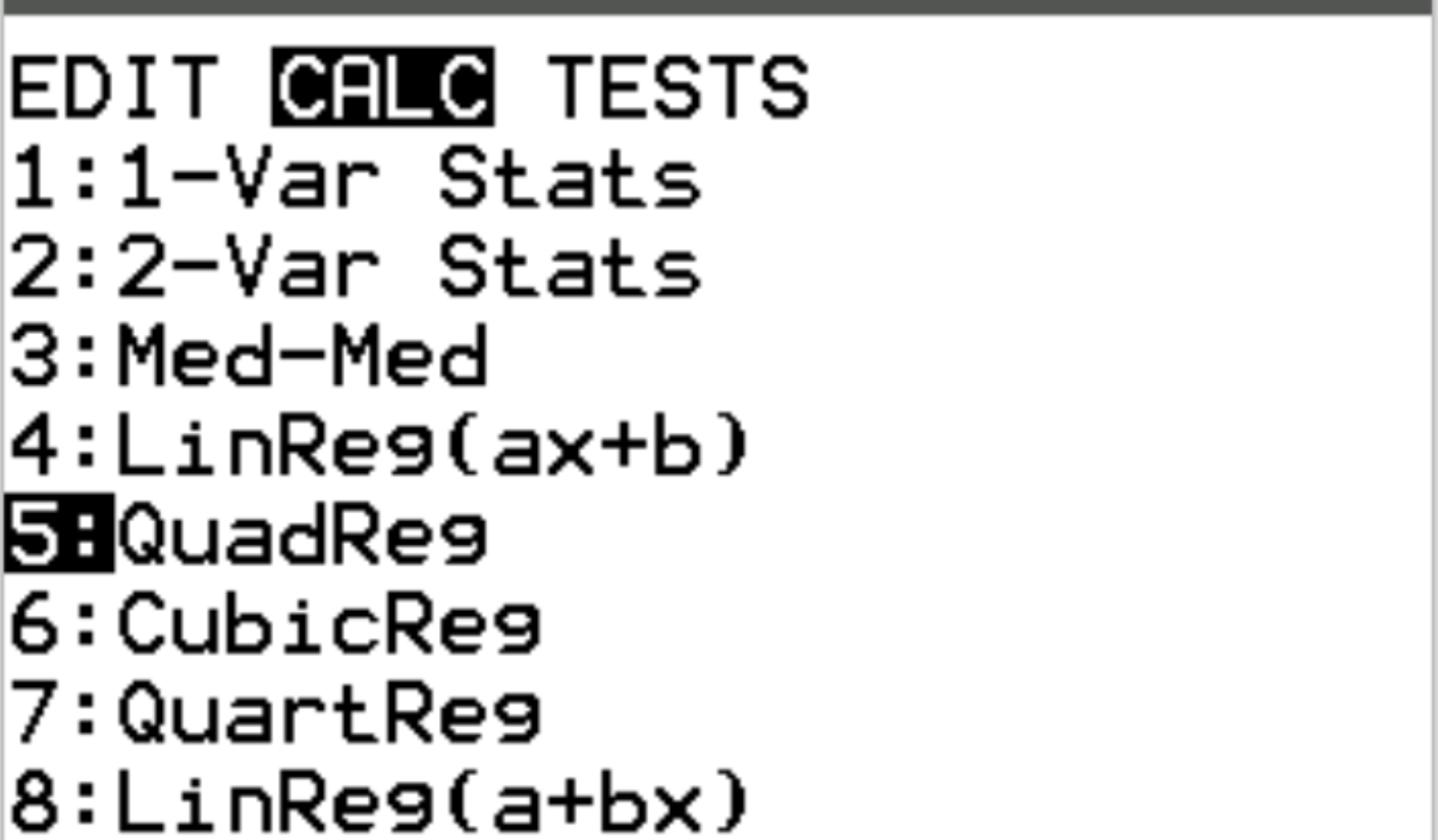
Als nächstes führen wir eine quadratische Regression durch. Drücken Sie Stat und scrollen Sie dann zu CALC . Scrollen Sie dann zu 5:QuadReg und drücken Sie die Eingabetaste .

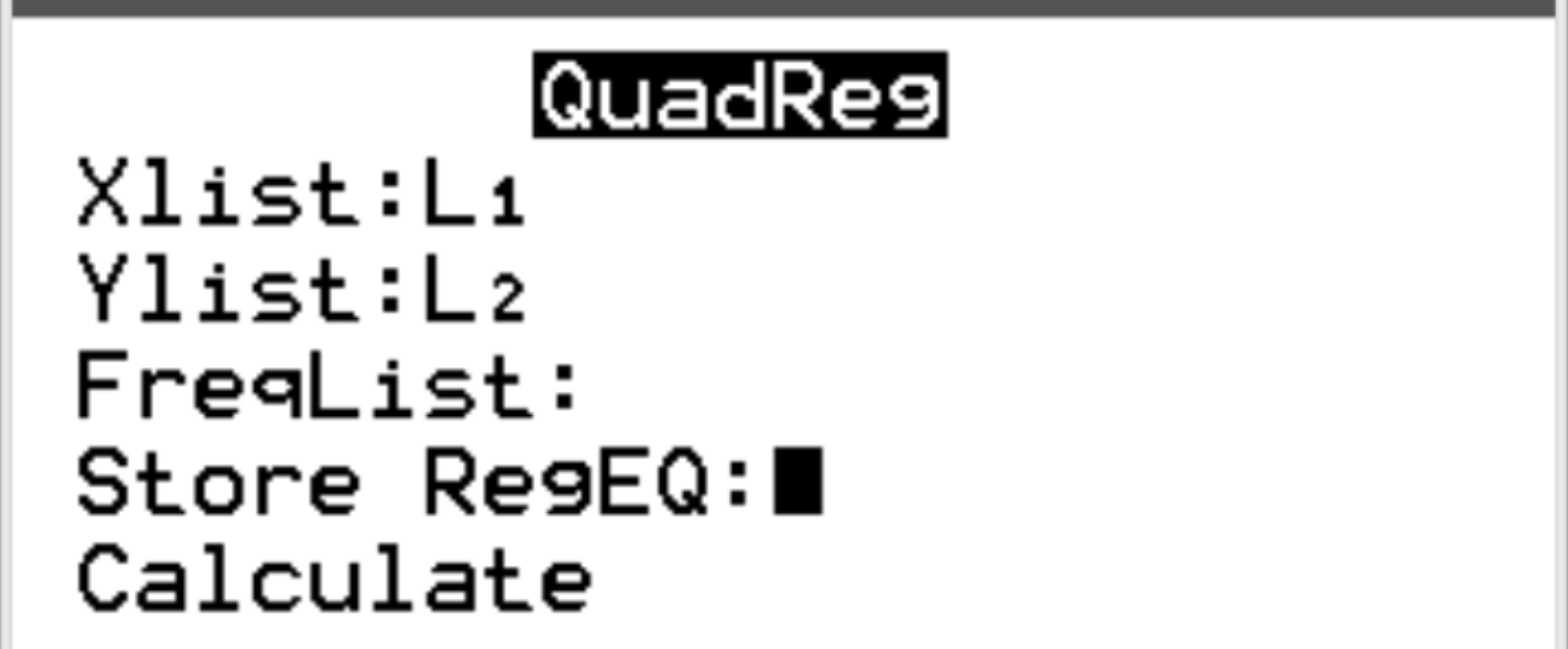
Stellen Sie sicher, dass für Xlist und Ylist L1 und L2 ausgewählt sind, da dies die Spalten sind, die wir zur Eingabe unserer Daten verwendet haben. Lassen Sie FreqList leer. Scrollen Sie nach unten zu Berechnen und drücken Sie die Eingabetaste .

Es erscheint automatisch folgende Ausgabe:

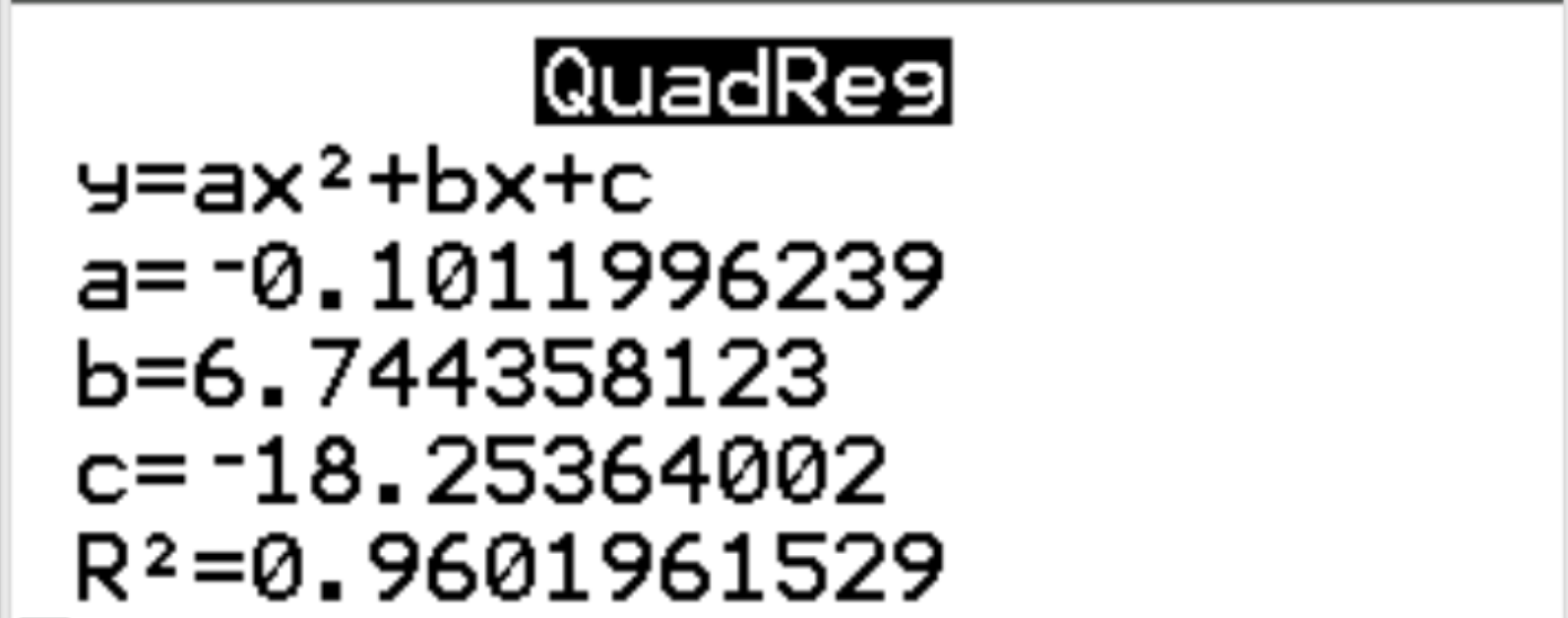
Schritt 3: Interpretieren Sie das Ergebnis.

Aus den Ergebnissen können wir ersehen, dass die geschätzte Regressionsgleichung lautet:

Glück = -0,1012 (Stunden) ² + 6,7444 (Stunden) – 18,2536

Mit dieser Gleichung können wir das prognostizierte Glück einer Person anhand der Anzahl der Stunden, die sie pro Woche arbeitet, ermitteln.

Beispielsweise hätte eine Person, die 60 Stunden pro Woche arbeitet, einen Glücksgrad von 22,09 :

Glück = -0,1012(60) ² + 6,7444(60) – 18,2536 = 22,09

Umgekehrt sollte eine Person, die 30 Stunden pro Woche arbeitet, einen Glücksgrad von 92,99 haben:

Glück = -0,1012(30) ² + 6,7444(30) – 18,2536 = 92,99

Wir können auch sehen, dass das r-Quadrat für das Regressionsmodell r ² = 0,9602 ist. Dies ist der Anteil der Varianz der Antwortvariablen, der durch die erklärenden Variablen erklärt werden kann. In diesem Beispiel können 96,02 % der Glücksschwankungen durch Stunden und Zeiten erklärt werden ² .