Tukey vs. bonferroni vs. scheffe: welchen test sollten sie verwenden?
Eine einfaktorielle ANOVA wird verwendet, um zu bestimmen, ob ein statistisch signifikanter Unterschied zwischen den Mittelwerten von drei oder mehr unabhängigen Gruppen besteht.
Wenn der Gesamt -p-Wert der ANOVA-Tabelle unter einem bestimmten Signifikanzniveau liegt, verfügen wir über ausreichende Beweise dafür, dass sich mindestens einer der Gruppenmittelwerte von den anderen unterscheidet.
Dies sagt uns jedoch nicht, welche Gruppen sich voneinander unterscheiden. Dies zeigt uns einfach, dass nicht alle Gruppendurchschnitte gleich sind.
Um genau zu wissen, welche Gruppen sich voneinander unterscheiden, müssen wir einenPost-hoc-Test durchführen, der die Fehlerrate pro Familie kontrollieren kann.
Zu den drei am häufigsten verwendeten Post-hoc-Tests gehören:
- Die Tukey-Methode
- Die Scheffe-Methode
- Die Bonferroni-Methode
Dieses Tutorial bietet einen Überblick über die einzelnen Methoden sowie Anweisungen, welcher Post-hoc-Test je nach Situation verwendet werden soll.
Die Tukey-Methode
Der Post-hoc-Test von Tukey sollte verwendet werden, wenn Sie paarweise Vergleiche zwischen Gruppen durchführen möchten, d. h. wenn die Stichprobengrößen jeder Gruppe gleich sind.
Wenn die Stichprobengrößen nicht gleich sind, können Sie eine modifizierte Version des Tests verwenden, den sogenannten Tukey-Kramer-Test.
Der Begriff „paarweise“ bedeutet, dass wir jeweils nur die Mittelwerte zweier Gruppen vergleichen möchten.
Angenommen, wir haben drei Gruppen: A, B, C.
Der Post-hoc-Test von Tukey würde es uns ermöglichen, die folgenden paarweisen Vergleiche durchzuführen:
- µA = µB
- µA = µC
- μB = μC
Beachten Sie, dass es für k Gruppen insgesamt k ( k -1)/2 mögliche paarweise Vergleiche gibt.
Die Scheffe-Methode
Der Scheffe-Post-hoc-Test sollte verwendet werden, wenn wir alle möglichen Kontraste zwischen den Gruppenmittelwerten ermitteln möchten. Mit diesem Test können Sie im Gegensatz zum Tukey-Post-hoc-Test mehr als zwei Mittelwerte gleichzeitig vergleichen.
Angenommen, wir haben vier Gruppen: A, B, C, D.
Der Scheffe-Post-hoc-Test würde komplexe Vergleiche ermöglichen, wie zum Beispiel:
- μA – μB = μC – μD
- μA + μD = μB + μC
Obwohl der Post-hoc-Test nach Scheffe am flexibelsten ist, ist er auch der konservativste und erzeugt die breitesten Konfidenzintervalle. Dies bedeutet, dass es die geringste statistische Aussagekraft und die geringste Fähigkeit aufweist, echte Unterschiede zwischen Gruppen zu erkennen.
Beachten Sie, dass der Scheffe-Post-hoc-Test unabhängig davon verwendet werden kann, ob die Stichprobengrößen der Gruppen gleich sind oder nicht.
Die Bonferroni-Methode
Der Bonferroni-Post-hoc-Test sollte verwendet werden, wenn Sie im Voraus eine Reihe geplanter Vergleiche durchführen möchten.
Angenommen, wir haben drei Gruppen – A, B, C – und wissen im Voraus, dass wir nur an den folgenden Vergleichen interessiert sind:
- µA = µB
- μB = μC
Wenn wir einen bestimmten Satz geplanter Vergleiche haben, die wir im Voraus wie diesen durchführen möchten, erzeugt der Bonferroni-Post-hoc-Test die engsten Konfidenzintervalle, was bedeutet, dass er die größte Fähigkeit hat, den wahren Unterschied zwischen Interessengruppen zu erkennen. .
Beachten Sie, dass der Bonferroni-Post-hoc-Test auch unabhängig davon verwendet werden kann, ob die Stichprobengrößen der Gruppen gleich sind oder nicht.
Welche Methode sollten Sie verwenden?
Der folgende Entscheidungsbaum hilft Ihnen, je nach Situation zu entscheiden, welchen Post-hoc-Test Sie verwenden sollten:
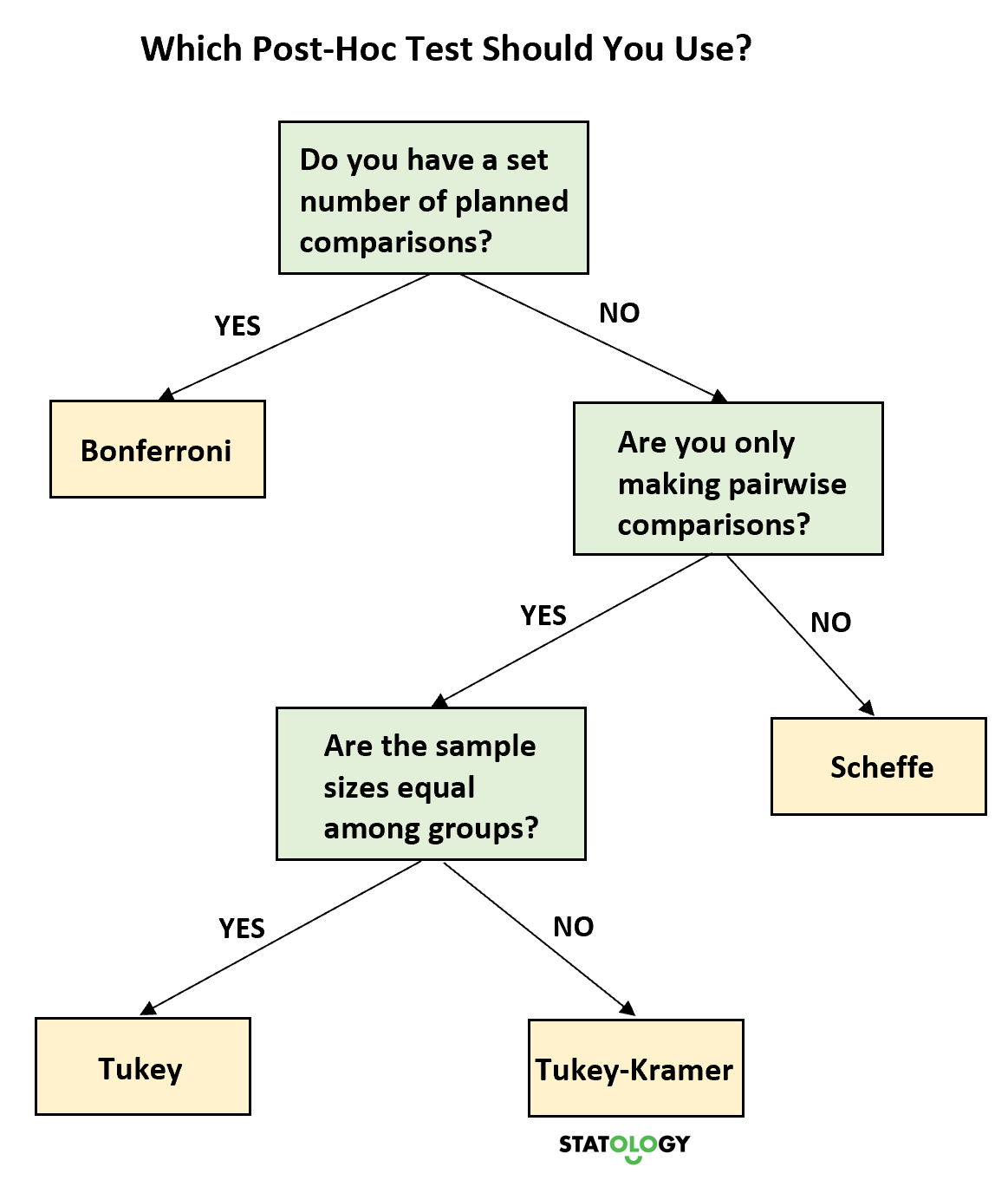
Abschließende Gedanken
Für welchen Post-hoc-Test Sie sich auch entscheiden, müssen Sie vor der Durchführung des Experiments entscheiden.
Dies verhindert, dass Sie nach dem Experiment einen Post-hoc-Test wählen, der mit größerer Wahrscheinlichkeit aussagekräftige Ergebnisse liefert, was als unehrliche Forschungspraxis angesehen wird.
Unabhängig davon sind die meisten Statistikprogramme in der Lage, diese Post-hoc-Tests durchzuführen, sodass Sie sie selten manuell berechnen müssen.